modwtLayer

Maximal overlap discrete wavelet transform layer

Since R2022b

Description

A MODWT layer computes the maximal overlap discrete wavelet transform (MODWT) and MODWT multiresolution analysis (MRA) of the input. Use of this layer requires Deep Learning Toolbox™.

Creation

Syntax

layer = modwtLayer

layer = modwtLayer(Name=Value)

Description

layer = modwtLayer creates a MODWT layer. By default, the layer computes the MODWTMRA to level 5 using the Daubechies least-asymmetric wavelet with four vanishing moments ('sym4').

The input to modwtLayer must be a real-valued dlarray (Deep Learning Toolbox) object in "CBT" format. The size of the time dimension of the tensor input must be greater than or equal to 2^Level, where Level is the transform level of the MODWT. modwtLayer formats the output as "SCBT". For more information, see Layer Output Format.

Note

The object initializes the weights internally for use as wavelet filters in the MODWT. It is not recommended to initialize the weights directly.

layer = modwtLayer(Name=Value) creates a MODWT layer with properties specified by name-value arguments. For example, layer = modwtLayer(Wavelet="haar") creates a MODWT layer that uses the Haar wavelet. You can specify the wavelet and the level of decomposition, among others.

example

Properties

expand all

MODWT

`Wavelet` — Orthogonal wavelet
`"sym4"` (default) | character vector | string scalar

This property is read-only.

Name of an orthogonal wavelet used in the MODWT, specified as a character vector or a string scalar.

Orthogonal wavelets are designated as type 1 wavelets in the wavelet manager. Valid built-in orthogonal wavelet families begin with 'haar', 'dbN', 'fkN', 'coifN', 'blN', 'hanSR.LP', 'symN', 'vaid', or 'beyl'. Use waveinfo with the wavelet family short name to see supported values for any numeric suffixes and how to interpret those values. For example, waveinfo("han").

For a wavelet specified by wname, the associated lowpass and highpass filters Lo and Hi, respectively, are [~,~,Lo,Hi] = wfilters(wname).

Data Types: char | string

`LowpassFilter` — Lowpass (scaling) filter
`[]` (default) | even-length real-valued vector

This property is read-only.

Lowpass (scaling) filter, specified as an even-length real-valued vector. LowpassFilter and HighpassFilter must have equal length and correspond to the lowpass and highpass filters associated with an orthogonal wavelet. You can use isorthwfb to determine orthogonality.

[~,~,Lo,Hi] = wfilters("db2");
[tf,checks] = isorthwfb(Lo,Hi);

If unspecified, both filters default to [] and modwtLayer uses Wavelet to determine the filters used in MODWT.

You cannot specify both a wavelet name and a wavelet filter pair.

Example: layer = modwtLayer('LowpassFilter',Lo,'HighpassFilter',Hi)

Data Types: single | double

`HighpassFilter` — Highpass (wavelet) filter
`[]` (default) | even-length real-valued vector

This property is read-only.

Highpass (wavelet) filter, specified as an even-length real-valued vector. LowpassFilter and HighpassFilter must have equal length and correspond to the lowpass and highpass filters associated with an orthogonal wavelet. You can use isorthwfb to determine orthogonality.

If unspecified, both filters default to [] and modwtLayer uses Wavelet to determine the filters used in MODWT.

You cannot specify both a wavelet name and a wavelet filter pair.

Data Types: single | double

`Level` — Transform level
`5` (default) | positive integer

This property is read-only.

Transform level to compute the MODWT, specified as a positive integer less than or equal to floor(log2(N)), where N is the size of the layer input in the time dimension.

Data Types: single | double

`Boundary` — Boundary condition
`"periodic"` (default) | `"reflection"`

This property is read-only.

Boundary condition to use in the computation of the MODWT, specified as one of these:

"periodic" — The signal is extended periodically along the time dimension. The number of wavelet coefficients equals the size of the signal in the time dimension.
"reflection" — The signal is reflected symmetrically along the time dimension at the terminal end before computing the MODWT. The number of wavelet coefficients returned is twice the length of the input signal.

`SelectedLevels` — Selected levels
`1:Level` (default) | vector

This property is read-only.

Selected levels for modwtLayer to output, specified as a vector of positive integers less than or equal to Level.

Data Types: single | double

`IncludeLowpass` — Include lowpass coefficients
`true` or `1` (default) | `false` or `0`

This property is read-only.

Include lowpass coefficients, specified as a numeric or logical 1 (true) or 0 (false). If specified as true, the MODWT layer includes the Levelth level lowpass (scaling) coefficients in the MODWT, or Levelth level smooth in the MODWTMRA.

Data Types: logical

`AggregateLevels` — Aggregate selected levels
`false` or `0` (default) | `true` or `1`

This property is read-only.

Aggregate selected levels, specified as a numeric or logical 1 (true) or 0 (false). If specified as true, the MODWT layer aggregates the selected levels and lowpass level (if IncludeLowpass is true) of each input channel by summation. If AggregateLevels is true, the size of the output in the spatial dimension is 1. For more information, Compare modwtLayer Output with modwt and modwtmra Outputs.

Data Types: logical

`Algorithm` — Algorithm
`"MODWTMRA"` (default) | `"MODWT"`

This property is read-only.

Algorithm modwtLayer uses to compute the output, specified as one of these:

"MODWTMRA" — Compute the maximal overlap discrete wavelet transform based multiresolution analysis.
"MODWT" — Compute the wavelet coefficients of the maximal overlap discrete wavelet transform.

For more information, see Comparing MODWT and MODWTMRA.

Layer

`WeightLearnRateFactor` — Multiplier for weight learning rate
`0` (default) | nonnegative scalar

Multiplier for weight learning rate, specified as a nonnegative scalar. If not specified, this property defaults to zero, resulting in weights that do not update with training. You can also set this property using the setLearnRateFactor (Deep Learning Toolbox) function.

The learnable parameter 'Weights' in modwtLayer is a two-row matrix of the current filter pair. The first row is the lowpass filter and the second row is the highpass filter. By default, the weights are the lowpass and highpass filters associated with the default wavelet and do not update.

Data Types: single | double

`Name` — Layer name
`""` (default) | character vector | string scalar

Layer name, specified as a character vector or string scalar. For Layer array input, the trainnet (Deep Learning Toolbox) and dlnetwork (Deep Learning Toolbox) functions automatically assign names to layers with the name "".

The modwtLayer object stores this property as a character vector.

Data Types: char | string

`NumInputs` — Number of inputs
`1` (default)

This property is read-only.

Number of inputs to the layer, returned as 1. This layer accepts a single input only.

Data Types: double

`InputNames` — Input names
`{'in'}` (default)

This property is read-only.

Input names, returned as {'in'}. This layer accepts a single input only.

Data Types: cell

`NumOutputs` — Number of outputs
`1` (default)

This property is read-only.

Number of outputs from the layer, returned as 1. This layer has a single output only.

Data Types: double

`OutputNames` — Output names
`{'out'}` (default)

This property is read-only.

Output names, returned as {'out'}. This layer has a single output only.

Data Types: cell

Examples

collapse all

Use `modwtLayer` in Deep Learning Network

This example uses:

Open Live Script

Create a MODWT layer to compute the multiresolution analysis for the input signal. Use a coiflet wavelet with order 5. Set the transform level to 8. Only keep the details at levels 3, 5, and 7, and the approximation.

layer = modwtLayer(Wavelet="coif5",Level=8, ...
    SelectedLevels=[3,5,7],Name="MODWT");

Create a dlnetwork object containing a sequence input layer, a MODWT layer, and an LSTM layer. For a level-8 decomposition, set the minimum sequence length to 2^8 samples. To work with an LSTM layer, a flatten layer is also needed before the LSTM layer to collapse the spatial dimension into the channel dimension.

mLength=2^8;
sqLayer = sequenceInputLayer(1,Name="input",MinLength=mLength);
layers = [sqLayer
    layer
    flattenLayer
    lstmLayer(10,Name="LSTM")
    ];
dlnet = dlnetwork(layers);

Run a batch of 10 random single-channel signals through the dlnetwork object. Inspect the size and dimensions of the output. The flatten layer has collapsed the spatial dimension.

dataout = dlnet.forward(dlarray(randn(1,10,2000,'single'),'CBT'));
size(dataout)

ans = 1×3

          10          10        2000

dims(dataout)

ans = 
'CBT'

Compare `modwtLayer` Output with `modwt` and `modwtmra` Outputs

This example uses:

Open Live Script

Load the Espiga3 electroencephalogram (EEG) dataset. The data consists of 23 channels of EEG sampled at 200 Hz. There are 995 samples in each channel. Save the multisignal as a dlarray, specifying the dimensions in order. dlarray permutes the array dimensions to the "CBT" shape expected by a deep learning network.

load Espiga3
[N,nch] = size(Espiga3);
x = dlarray(Espiga3,"TCB");

Use modwt and modwtmra to obtain the MODWT and MRA of the multisignal down to level 6. By default, modwt and modwtmra use the sym4 wavelet.

lev = 6;
wt = modwt(Espiga3,lev);
mra = modwtmra(wt);

Compare with modwt

Create a MODWT layer that can be used with the data. Set the transform level to 6. Specify the layer to use MODWT to compute the output. By default, the layer uses the sym4 wavelet.

mlayer = modwtLayer(Level=lev,Algorithm="MODWT");

Create a two-layer dlnetwork object containing a sequence input layer and the MODWT layer you just created. Treat each channel as a feature. For a level-6 decomposition, set the minimum sequence length to 2^6.

mLength = mlayer.Level;
sqInput = sequenceInputLayer(nch,MinLength=2^mLength);
layers = [sqInput
    mlayer];
dlnet = dlnetwork(layers);

Run the EEG data through the forward method of the network.

dataout = forward(dlnet,x);

The modwt and modwtmra functions return the MODWT and MRA of a multichannel signal as a 3-D array. The first, second, and third dimensions of the array correspond to the wavelet decomposition level, signal length, and channel, respectively. Convert the network output to a numeric array. Permute the dimensions of the network output to match the function output. Compare the network output with the modwt output.

q = extractdata(dataout);
q = permute(q,[1 4 2 3]);
max(abs(q(:)-wt(:)))

ans = 
8.4402e-05

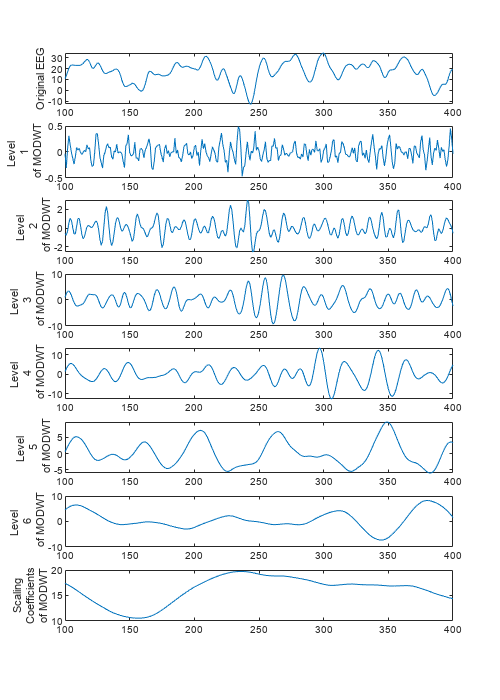
Choose a MODWT result from modwtLayer. Compare with the corresponding channel in the EEG data. Plot each level of the modwtLayer output. Different levels contain information about the signal in different frequency ranges. The levels are not time aligned with the original signal because the layer uses the MODWT algorithm.

channel = 10;
t = 100:400;
subplot(lev+2,1,1)
plot(t,Espiga3(t,channel))
ylabel("Original EEG")
for k=2:lev+1
    subplot(lev+2,1,k)
    plot(t,q(k-1,t,channel))
    ylabel(["Level ",k-1," of MODWT"])
end
subplot(lev+2,1,lev+2)
plot(t,q(lev+1,t,channel))
ylabel(["Scaling","Coefficients","of MODWT"])
set(gcf,Position=[0 0 500 700])

Compare with modwtmra

Create a second network similar to the first network, except this time specify that modwtLayer use the MODWTMRA algorithm and aggregate the fourth, fifth, and sixth levels. Do not include the lowpass level in the aggregation.

sLevels = [4 5 6];
mlayer = modwtLayer(Level=lev, ...
    SelectedLevels=sLevels, ...
    IncludeLowpass=0, ...
    AggregateLevels=1);
layers = [sqInput
    mlayer];
dlnet2 = dlnetwork(layers);

Run the EEG data through the forward method of the network. Convert the network output to a numeric array. Permute the dimensions as done previously.

dataout = forward(dlnet2,x);
q = extractdata(dataout);
q = permute(q,[1 4 3 2]);

Aggregate the fourth, fifth, and sixth levels of the MRA. Compare with the network output.

mraAggregate = sum(mra(sLevels,:,:));
max(abs(q(:)-mraAggregate(:)))

ans = 
2.1036e-04

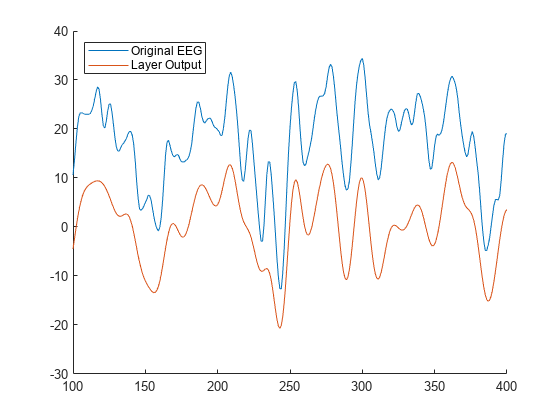
Inspect a MODWTMRA result from the layer. Compare with the corresponding channel in the EEG data. By choosing only the fourth, fifth, and six levels, and not including the lowpass component, the layer removes several high and low frequency components from the signal. The transformed signal is smoother than the original signal and the low frequency components are removed so that the offset is closer to 0. The output is time aligned with the original signal because the layer uses the default MODWTMRA algorithm. Depending on your goal, preserving time alignment can be useful.

channel = 10;
t = 100:400;
figure
hold on
plot(t, Espiga3(t,channel))
plot(t,q(1,t,1,channel))
hold off
legend(["Original EEG", "Layer Output"], ...
    Location="northwest")

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Original EEG, Layer Output.

More About

expand all

Layer Output Format

modwtLayer formats the output as "SCBT", a sequence of 1-D images where the image height corresponds to the level of the wavelet transform, the second dimension corresponds to the channel, the third dimension corresponds to the batch, and the fourth dimension corresponds to time. The kth row, where k ≤ Level, contains the kth level detail of the signal. The (Level+1)th row contains the Levelth level smooth of the signal.

You can feed the output of modwtLayer unchanged to a 1-D convolutional layer when you want to convolve along the level ("S") dimension. For more information, see convolution1dLayer (Deep Learning Toolbox).
To feed the output of modwtLayer to a 1-D convolutional layer when you want to convolve along the time ("T") dimension, you must place a flatten layer after the modwtLayer. For more information, see flattenLayer (Deep Learning Toolbox).
You can feed the output of modwtLayer unchanged to a 2-D convolutional layer when you want to convolve along the level ("S") and time ("T") dimensions jointly. For more information, see convolution2dLayer (Deep Learning Toolbox).
To use modwtLayer as part of a recurrent neural network, you must place a flatten layer after the modwtLayer. For more information, see lstmLayer (Deep Learning Toolbox) and gruLayer (Deep Learning Toolbox).
To use the output of modwtLayer with a fully connected layer as part of a classification workflow, you must reduce the time ("T") dimension of the output so that it is of size 1. To reduce the time dimension of the output, place a global pooling layer before the fully connected layer. For more information, see globalAveragePooling2dLayer (Deep Learning Toolbox) and fullyConnectedLayer (Deep Learning Toolbox).

Version History

Introduced in R2022b

modwtLayer

Description

Creation

Syntax

Description

Properties

MODWT

`Wavelet` — Orthogonal wavelet
`"sym4"` (default) | character vector | string scalar

`LowpassFilter` — Lowpass (scaling) filter
`[]` (default) | even-length real-valued vector

`HighpassFilter` — Highpass (wavelet) filter
`[]` (default) | even-length real-valued vector

`Level` — Transform level
`5` (default) | positive integer

`Boundary` — Boundary condition
`"periodic"` (default) | `"reflection"`

`SelectedLevels` — Selected levels
`1:Level` (default) | vector

`IncludeLowpass` — Include lowpass coefficients
`true` or `1` (default) | `false` or `0`

`AggregateLevels` — Aggregate selected levels
`false` or `0` (default) | `true` or `1`

`Algorithm` — Algorithm
`"MODWTMRA"` (default) | `"MODWT"`

Layer

`WeightLearnRateFactor` — Multiplier for weight learning rate
`0` (default) | nonnegative scalar

`Name` — Layer name
`""` (default) | character vector | string scalar

`NumInputs` — Number of inputs
`1` (default)

`InputNames` — Input names
`{'in'}` (default)

`NumOutputs` — Number of outputs
`1` (default)

`OutputNames` — Output names
`{'out'}` (default)

Examples

Use `modwtLayer` in Deep Learning Network

Compare `modwtLayer` Output with `modwt` and `modwtmra` Outputs

More About

Layer Output Format

Version History

See Also

Apps

Functions

Objects

Topics

modwtLayer

Description

Creation

Syntax

Description

Properties

MODWT

Wavelet — Orthogonal wavelet "sym4" (default) | character vector | string scalar

LowpassFilter — Lowpass (scaling) filter [] (default) | even-length real-valued vector

HighpassFilter — Highpass (wavelet) filter [] (default) | even-length real-valued vector

Level — Transform level 5 (default) | positive integer

Boundary — Boundary condition "periodic" (default) | "reflection"

SelectedLevels — Selected levels 1:Level (default) | vector

IncludeLowpass — Include lowpass coefficients true or 1 (default) | false or 0

AggregateLevels — Aggregate selected levels false or 0 (default) | true or 1

Algorithm — Algorithm "MODWTMRA" (default) | "MODWT"

Layer

WeightLearnRateFactor — Multiplier for weight learning rate 0 (default) | nonnegative scalar

Name — Layer name "" (default) | character vector | string scalar

NumInputs — Number of inputs 1 (default)

InputNames — Input names {'in'} (default)

NumOutputs — Number of outputs 1 (default)

OutputNames — Output names {'out'} (default)

Examples

Use modwtLayer in Deep Learning Network

Compare modwtLayer Output with modwt and modwtmra Outputs

More About

Layer Output Format

Version History

See Also

Apps

Functions

Objects

Topics

`Wavelet` — Orthogonal wavelet
`"sym4"` (default) | character vector | string scalar

`LowpassFilter` — Lowpass (scaling) filter
`[]` (default) | even-length real-valued vector

`HighpassFilter` — Highpass (wavelet) filter
`[]` (default) | even-length real-valued vector

`Level` — Transform level
`5` (default) | positive integer

`Boundary` — Boundary condition
`"periodic"` (default) | `"reflection"`

`SelectedLevels` — Selected levels
`1:Level` (default) | vector

`IncludeLowpass` — Include lowpass coefficients
`true` or `1` (default) | `false` or `0`

`AggregateLevels` — Aggregate selected levels
`false` or `0` (default) | `true` or `1`

`Algorithm` — Algorithm
`"MODWTMRA"` (default) | `"MODWT"`

`WeightLearnRateFactor` — Multiplier for weight learning rate
`0` (default) | nonnegative scalar

`Name` — Layer name
`""` (default) | character vector | string scalar

`NumInputs` — Number of inputs
`1` (default)

`InputNames` — Input names
`{'in'}` (default)

`NumOutputs` — Number of outputs
`1` (default)

`OutputNames` — Output names
`{'out'}` (default)

Use `modwtLayer` in Deep Learning Network

Compare `modwtLayer` Output with `modwt` and `modwtmra` Outputs