convolution2dLayer

2-D convolutional layer

Description

A 2-D convolutional layer applies sliding convolutional filters to 2-D input. The layer convolves the input by moving the filters along the input vertically and horizontally and computing the dot product of the weights and the input, and then adding a bias term.

The dimensions that the layer convolves over depends on the layer input:

For 2-D image input (data with four dimensions corresponding to pixels in two spatial dimensions, the channels, and the observations), the layer convolves over the spatial dimensions.
For 2-D image sequence input (data with five dimensions corresponding to the pixels in two spatial dimensions, the channels, the observations, and the time steps), the layer convolves over the two spatial dimensions.
For 1-D image sequence input (data with four dimensions corresponding to the pixels in one spatial dimension, the channels, the observations, and the time steps), the layer convolves over the spatial and time dimensions.

Creation

Syntax

layer = convolution2dLayer(filterSize,numFilters)

layer = convolution2dLayer(filterSize,numFilters,Name=Value)

Description

layer = convolution2dLayer(filterSize,numFilters) creates a 2-D convolutional layer and sets the FilterSize and NumFilters properties.

layer = convolution2dLayer(filterSize,numFilters,Name=Value) sets optional properties using one or more name-value arguments.

example

Input Arguments

expand all

`filterSize` — Height and width of filters
vector of two positive integers | positive integer

Height and width of the filters, specified as a vector [h w] of two positive integers, where h is the height and w is the width. filterSize defines the size of the local regions to which the neurons connect in the input.

When you create the layer, you can specify filterSize as a scalar to use the same value for the height and width.

Example: [5 5] specifies filters with a height of 5 and a width of 5.

`numFilters` — Number of filters
positive integer

Number of filters, specified as a positive integer. This number corresponds to the number of neurons in the layer that connect to the same region in the input. This parameter determines the number of channels (feature maps) in the layer output.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: convolution2dLayer(3,16,Padding="same") creates a 2-D convolutional layer with 16 filters of size [3 3] and 'same' padding. At training time, the software calculates and sets the size of the padding so that the layer output has the same size as the input.

`Stride` — Step size for traversing input
`[1 1]` (default) | vector of two positive integers | positive integer

Step size for traversing the input vertically and horizontally, specified as a vector [a b] of two positive integers, where a is the vertical step size and b is the horizontal step size. When creating the layer, you can specify Stride as a scalar to use the same value for both step sizes.

Example: [2 3] specifies a vertical step size of 2 and a horizontal step size of 3.

`DilationFactor` — Factor for dilated convolution
`[1 1]` (default) | vector of two positive integers | positive integer

Factor for dilated convolution (also known as atrous convolution), specified as a vector [h w] of two positive integers, where h is the vertical dilation and w is the horizontal dilation. When creating the layer, you can specify DilationFactor as a scalar to use the same value for both horizontal and vertical dilations.

Use dilated convolutions to increase the receptive field (the area of the input which the layer can see) of the layer without increasing the number of parameters or computation.

The layer expands the filters by inserting zeros between each filter element. The dilation factor determines the step size for sampling the input or equivalently the upsampling factor of the filter. It corresponds to an effective filter size of (Filter Size – 1) .* Dilation Factor + 1. For example, a 3-by-3 filter with the dilation factor [2 2] is equivalent to a 5-by-5 filter with zeros between the elements.

Example: [2 3]

`Padding` — Input edge padding
`[0 0 0 0]` (default) | vector of nonnegative integers | `"same"`

Input edge padding, specified as one of these values:

"same" — Add padding of size calculated by the software at training or prediction time so that the output has the same size as the input when the stride equals 1. If the stride is larger than 1, then the output size is ceil(inputSize/stride), where inputSize is the height or width of the input and stride is the stride in the corresponding dimension. The software adds the same amount of padding to the top and bottom, and to the left and right, if possible. If the padding that must be added vertically has an odd value, then the software adds extra padding to the bottom. If the padding that must be added horizontally has an odd value, then the software adds extra padding to the right.
Nonnegative integer p — Add padding of size p to all the edges of the input.
Vector [a b] of nonnegative integers — Add padding of size a to the top and bottom of the input and padding of size b to the left and right.
Vector [t b l r] of nonnegative integers — Add padding of size t to the top, b to the bottom, l to the left, and r to the right of the input.

Example: Padding=1 adds one row of padding to the top and bottom, and one column of padding to the left and right of the input.

Example: Padding="same" adds padding so that the output has the same size as the input (if the stride equals 1).

`PaddingValue` — Value to pad data
0 (default) | scalar | `"symmetric-include-edge"` | `"symmetric-exclude-edge"` | `"replicate"`

Value to pad data, specified as one of the following:

`PaddingValue`	Description	Example
Scalar	Pad with the specified scalar value.	$[\begin{matrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \end{matrix}] \to [\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 3 & 1 & 4 & 0 & 0 \\ 0 & 0 & 1 & 5 & 9 & 0 & 0 \\ 0 & 0 & 2 & 6 & 5 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]$
`"symmetric-include-edge"`	Pad using mirrored values of the input, including the edge values.	$[\begin{matrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \end{matrix}] \to [\begin{matrix} 5 & 1 & 1 & 5 & 9 & 9 & 5 \\ 1 & 3 & 3 & 1 & 4 & 4 & 1 \\ 1 & 3 & 3 & 1 & 4 & 4 & 1 \\ 5 & 1 & 1 & 5 & 9 & 9 & 5 \\ 6 & 2 & 2 & 6 & 5 & 5 & 6 \\ 6 & 2 & 2 & 6 & 5 & 5 & 6 \\ 5 & 1 & 1 & 5 & 9 & 9 & 5 \end{matrix}]$
`"symmetric-exclude-edge"`	Pad using mirrored values of the input, excluding the edge values.	$[\begin{matrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \end{matrix}] \to [\begin{matrix} 5 & 6 & 2 & 6 & 5 & 6 & 2 \\ 9 & 5 & 1 & 5 & 9 & 5 & 1 \\ 4 & 1 & 3 & 1 & 4 & 1 & 3 \\ 9 & 5 & 1 & 5 & 9 & 5 & 1 \\ 5 & 6 & 2 & 6 & 5 & 6 & 2 \\ 9 & 5 & 1 & 5 & 9 & 5 & 1 \\ 4 & 1 & 3 & 1 & 4 & 1 & 3 \end{matrix}]$
`"replicate"`	Pad using repeated border elements of the input	$[\begin{matrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \end{matrix}] \to [\begin{matrix} 3 & 3 & 3 & 1 & 4 & 4 & 4 \\ 3 & 3 & 3 & 1 & 4 & 4 & 4 \\ 3 & 3 & 3 & 1 & 4 & 4 & 4 \\ 1 & 1 & 1 & 5 & 9 & 9 & 9 \\ 2 & 2 & 2 & 6 & 5 & 5 & 5 \\ 2 & 2 & 2 & 6 & 5 & 5 & 5 \\ 2 & 2 & 2 & 6 & 5 & 5 & 5 \end{matrix}]$

`NumChannels` — Number of input channels
`"auto"` (default) | positive integer

Number of input channels, specified as one of the following:

"auto" — Automatically determine the number of input channels at training time.
Positive integer — Configure the layer for the specified number of input channels. NumChannels and the number of channels in the layer input data must match. For example, if the input is an RGB image, then NumChannels must be 3. If the input is the output of a convolutional layer with 16 filters, then NumChannels must be 16.

`WeightsInitializer` — Function to initialize weights
`"glorot"` (default) | `"he"` | `"narrow-normal"` | `"zeros"` | `"ones"` | function handle

Function to initialize the weights, specified as one of the following:

"glorot" – Initialize the weights with the Glorot initializer [4] (also known as Xavier initializer). The Glorot initializer independently samples from a uniform distribution with zero mean and variance 2/(numIn + numOut), where numIn = FilterSize(1)*FilterSize(2)*NumChannels and numOut = FilterSize(1)*FilterSize(2)*NumFilters.
"he" – Initialize the weights with the He initializer [5]. The He initializer samples from a normal distribution with zero mean and variance 2/numIn, where numIn = FilterSize(1)*FilterSize(2)*NumChannels.
"narrow-normal" – Initialize the weights by independently sampling from a normal distribution with zero mean and standard deviation 0.01.
"zeros" – Initialize the weights with zeros.
"ones" – Initialize the weights with ones.
Function handle – Initialize the weights with a custom function. If you specify a function handle, then the function must be of the form weights = func(sz), where sz is the size of the weights. For an example, see Specify Custom Weight Initialization Function.

The layer only initializes the weights when the Weights property is empty.

Data Types: char | string | function_handle

`BiasInitializer` — Function to initialize biases
`"zeros"` (default) | `"narrow-normal"` | `"ones"` | function handle

Function to initialize the biases, specified as one of these values:

"zeros" — Initialize the biases with zeros.
"ones" — Initialize the biases with ones.
"narrow-normal" — Initialize the biases by independently sampling from a normal distribution with a mean of zero and a standard deviation of 0.01.
Function handle — Initialize the biases with a custom function. If you specify a function handle, then the function must have the form bias = func(sz), where sz is the size of the biases.

The layer initializes the biases only when the Bias property is empty.

Data Types: char | string | function_handle

`Weights` — Layer weights
`[]` (default) | numeric array

Layer weights for the convolutional layer, specified as a numeric array.

The layer weights are learnable parameters. You can specify the initial value of the weights directly using the Weights property of the layer. When you train a network, if the Weights property of the layer is nonempty, then the trainnet function uses the Weights property as the initial value. If the Weights property is empty, then the software uses the initializer specified by the WeightsInitializer property of the layer.

At training time, Weights is a FilterSize(1)-by-FilterSize(2)-by-NumChannels-by-NumFilters array.

Data Types: single | double

`Bias` — Layer biases
`[]` (default) | numeric array

Layer biases for the convolutional layer, specified as a numeric array.

The layer biases are learnable parameters. When you train a neural network, if Bias is nonempty, then the trainnet and trainNetwork functions use the Bias property as the initial value. If Bias is empty, then software uses the initializer specified by BiasInitializer.

At training time, Bias is a 1-by-1-by-NumFilters array.

Data Types: single | double

`WeightLearnRateFactor` — Learning rate factor for weights
`1` (default) | nonnegative scalar

Learning rate factor for the weights, specified as a nonnegative scalar.

The software multiplies this factor by the global learning rate to determine the learning rate for the weights in this layer. For example, if WeightLearnRateFactor is 2, then the learning rate for the weights in this layer is twice the current global learning rate. The software determines the global learning rate based on the settings you specify using the trainingOptions function.

`BiasLearnRateFactor` — Learning rate factor for biases
`1` (default) | nonnegative scalar

Learning rate factor for the biases, specified as a nonnegative scalar.

The software multiplies this factor by the global learning rate to determine the learning rate for the biases in this layer. For example, if BiasLearnRateFactor is 2, then the learning rate for the biases in the layer is twice the current global learning rate. The software determines the global learning rate based on the settings you specify using the trainingOptions function.

`WeightL2Factor` — L₂ regularization factor for weights
1 (default) | nonnegative scalar

L₂ regularization factor for the weights, specified as a nonnegative scalar.

The software multiplies this factor by the global L₂ regularization factor to determine the L₂ regularization for the weights in this layer. For example, if WeightL2Factor is 2, then the L₂ regularization for the weights in this layer is twice the global L₂ regularization factor. You can specify the global L₂ regularization factor using the trainingOptions function.

`BiasL2Factor` — L₂ regularization factor for biases
`0` (default) | nonnegative scalar

L₂ regularization factor for the biases, specified as a nonnegative scalar.

The software multiplies this factor by the global L₂ regularization factor to determine the L₂ regularization for the biases in this layer. For example, if BiasL2Factor is 2, then the L₂ regularization for the biases in this layer is twice the global L₂ regularization factor. The software determines the global L₂ regularization factor based on the settings you specify using the trainingOptions function.

`Name` — Layer name
`""` (default) | character vector | string scalar

Layer name, specified as a character vector or a string scalar. For Layer array input, the trainnet and dlnetwork functions automatically assign names to layers with the name "".

The Convolution2DLayer object stores the Name property as a character vector.

Data Types: char | string

Properties

expand all

2-D Convolution

`FilterSize` — Height and width of filters
vector of two positive integers

Height and width of the filters, specified as a vector [h w] of two positive integers, where h is the height and w is the width. FilterSize defines the size of the local regions to which the neurons connect in the input.

When you create the layer, you can specify FilterSize as a scalar to use the same value for the height and width.

Example: [5 5] specifies filters with a height of 5 and a width of 5.

`NumFilters` — Number of filters
positive integer

This property is read-only.

`Stride` — Step size for traversing input
`[1 1]` (default) | vector of two positive integers

Example: [2 3] specifies a vertical step size of 2 and a horizontal step size of 3.

`DilationFactor` — Factor for dilated convolution
`[1 1]` (default) | vector of two positive integers

Use dilated convolutions to increase the receptive field (the area of the input which the layer can see) of the layer without increasing the number of parameters or computation.

Example: [2 3]

`PaddingSize` — Size of padding
`[0 0 0 0]` (default) | vector of four nonnegative integers

Size of padding to apply to input borders, specified as a vector [t b l r] of four nonnegative integers, where t is the padding applied to the top, b is the padding applied to the bottom, l is the padding applied to the left, and r is the padding applied to the right.

When you create a layer, use the 'Padding' name-value pair argument to specify the padding size.

Example: [1 1 2 2] adds one row of padding to the top and bottom, and two columns of padding to the left and right of the input.

`PaddingMode` — Method to determine padding size
`"manual"` (default) | `"same"`

Method to determine padding size, specified as "manual" or "same".

The software automatically sets the value of PaddingMode based on the Padding value you specify when creating a layer.

If you set the Padding option to a scalar or a vector of nonnegative integers, then the software automatically sets PaddingMode to "manual".
If you set the Padding option to "same", then the software automatically sets PaddingMode to 'same' and calculates the size of the padding at training time so that the output has the same size as the input when the stride equals 1. If the stride is larger than 1, then the output size is ceil(inputSize/stride), where inputSize is the height or width of the input and stride is the stride in the corresponding dimension. The software adds the same amount of padding to the top and bottom, and to the left and right, if possible. If the padding that must be added vertically has an odd value, then the software adds extra padding to the bottom. If the padding that must be added horizontally has an odd value, then the software adds extra padding to the right.

`Padding` — Size of padding
`[0 0]` (default) | vector of two nonnegative integers

Note

Padding property will be removed in a future release. Use PaddingSize instead. When creating a layer, use the Padding name-value argument to specify the padding size.

Size of padding to apply to input borders vertically and horizontally, specified as a vector [a b] of two nonnegative integers, where a is the padding applied to the top and bottom of the input data and b is the padding applied to the left and right.

Example: [1 1] adds one row of padding to the top and bottom, and one column of padding to the left and right of the input.

`PaddingValue` — Value to pad data
0 (default) | scalar | `"symmetric-include-edge"` | `"symmetric-exclude-edge"` | `"replicate"`

Value to pad data, specified as one of these values:

`PaddingValue`	Description	Example
Scalar	Pad with the specified scalar value.	$[\begin{matrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \end{matrix}] \to [\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 3 & 1 & 4 & 0 & 0 \\ 0 & 0 & 1 & 5 & 9 & 0 & 0 \\ 0 & 0 & 2 & 6 & 5 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]$
`"symmetric-include-edge"`	Pad using mirrored values of the input, including the edge values.	$[\begin{matrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \end{matrix}] \to [\begin{matrix} 5 & 1 & 1 & 5 & 9 & 9 & 5 \\ 1 & 3 & 3 & 1 & 4 & 4 & 1 \\ 1 & 3 & 3 & 1 & 4 & 4 & 1 \\ 5 & 1 & 1 & 5 & 9 & 9 & 5 \\ 6 & 2 & 2 & 6 & 5 & 5 & 6 \\ 6 & 2 & 2 & 6 & 5 & 5 & 6 \\ 5 & 1 & 1 & 5 & 9 & 9 & 5 \end{matrix}]$
`"symmetric-exclude-edge"`	Pad using mirrored values of the input, excluding the edge values.	$[\begin{matrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \end{matrix}] \to [\begin{matrix} 5 & 6 & 2 & 6 & 5 & 6 & 2 \\ 9 & 5 & 1 & 5 & 9 & 5 & 1 \\ 4 & 1 & 3 & 1 & 4 & 1 & 3 \\ 9 & 5 & 1 & 5 & 9 & 5 & 1 \\ 5 & 6 & 2 & 6 & 5 & 6 & 2 \\ 9 & 5 & 1 & 5 & 9 & 5 & 1 \\ 4 & 1 & 3 & 1 & 4 & 1 & 3 \end{matrix}]$
`"replicate"`	Pad using repeated border elements of the input	$[\begin{matrix} 3 & 1 & 4 \\ 1 & 5 & 9 \\ 2 & 6 & 5 \end{matrix}] \to [\begin{matrix} 3 & 3 & 3 & 1 & 4 & 4 & 4 \\ 3 & 3 & 3 & 1 & 4 & 4 & 4 \\ 3 & 3 & 3 & 1 & 4 & 4 & 4 \\ 1 & 1 & 1 & 5 & 9 & 9 & 9 \\ 2 & 2 & 2 & 6 & 5 & 5 & 5 \\ 2 & 2 & 2 & 6 & 5 & 5 & 5 \\ 2 & 2 & 2 & 6 & 5 & 5 & 5 \end{matrix}]$

`NumChannels` — Number of input channels
`"auto"` (default) | positive integer

This property is read-only.

Number of input channels, specified as one of the following:

"auto" — Automatically determine the number of input channels at training time.
Positive integer — Configure the layer for the specified number of input channels. NumChannels and the number of channels in the layer input data must match. For example, if the input is an RGB image, then NumChannels must be 3. If the input is the output of a convolutional layer with 16 filters, then NumChannels must be 16.

Parameters and Initialization

`WeightsInitializer` — Function to initialize weights
`"glorot"` (default) | `"he"` | `"narrow-normal"` | `"zeros"` | `"ones"` | function handle

Function to initialize the weights, specified as one of the following:

"glorot" – Initialize the weights with the Glorot initializer [4] (also known as Xavier initializer). The Glorot initializer independently samples from a uniform distribution with zero mean and variance 2/(numIn + numOut), where numIn = FilterSize(1)*FilterSize(2)*NumChannels and numOut = FilterSize(1)*FilterSize(2)*NumFilters.
"he" – Initialize the weights with the He initializer [5]. The He initializer samples from a normal distribution with zero mean and variance 2/numIn, where numIn = FilterSize(1)*FilterSize(2)*NumChannels.
"narrow-normal" – Initialize the weights by independently sampling from a normal distribution with zero mean and standard deviation 0.01.
"zeros" – Initialize the weights with zeros.
"ones" – Initialize the weights with ones.
Function handle – Initialize the weights with a custom function. If you specify a function handle, then the function must be of the form weights = func(sz), where sz is the size of the weights. For an example, see Specify Custom Weight Initialization Function.

The layer only initializes the weights when the Weights property is empty.

Data Types: char | string | function_handle

`BiasInitializer` — Function to initialize biases
`"zeros"` (default) | `"narrow-normal"` | `"ones"` | function handle

Function to initialize the biases, specified as one of these values:

"zeros" — Initialize the biases with zeros.
"ones" — Initialize the biases with ones.
"narrow-normal" — Initialize the biases by independently sampling from a normal distribution with a mean of zero and a standard deviation of 0.01.
Function handle — Initialize the biases with a custom function. If you specify a function handle, then the function must have the form bias = func(sz), where sz is the size of the biases.

The layer initializes the biases only when the Bias property is empty.

The Convolution2DLayer object stores this property as a character vector or a function handle.

Data Types: char | string | function_handle

`Weights` — Layer weights
`[]` (default) | numeric array

Layer weights for the convolutional layer, specified as a numeric array.

At training time, Weights is a FilterSize(1)-by-FilterSize(2)-by-NumChannels-by-NumFilters array.

Data Types: single | double

`Bias` — Layer biases
`[]` (default) | numeric array

Layer biases for the convolutional layer, specified as a numeric array.

The layer biases are learnable parameters. When you train a neural network, if Bias is nonempty, then the trainnet function uses the Bias property as the initial value. If Bias is empty, then software uses the initializer specified by BiasInitializer.

At training time, Bias is a 1-by-1-by-NumFilters array.

Data Types: single | double

Learning Rate and Regularization

`WeightLearnRateFactor` — Learning rate factor for weights
`1` (default) | nonnegative scalar

Learning rate factor for the weights, specified as a nonnegative scalar.

`BiasLearnRateFactor` — Learning rate factor for biases
`1` (default) | nonnegative scalar

Learning rate factor for the biases, specified as a nonnegative scalar.

`WeightL2Factor` — L₂ regularization factor for weights
1 (default) | nonnegative scalar

L₂ regularization factor for the weights, specified as a nonnegative scalar.

`BiasL2Factor` — L₂ regularization factor for biases
`0` (default) | nonnegative scalar

L₂ regularization factor for the biases, specified as a nonnegative scalar.

Layer

`Name` — Layer name
`""` (default) | character vector | string scalar

Layer name, specified as a character vector or string scalar. For Layer array input, the trainnet and dlnetwork functions automatically assign names to layers with the name "".

The Convolution2DLayer object stores this property as a character vector.

Data Types: char | string

`NumInputs` — Number of inputs
`1` (default)

This property is read-only.

Number of inputs to the layer, returned as 1. This layer accepts a single input only.

Data Types: double

`InputNames` — Input names
`{'in'}` (default)

This property is read-only.

Input names, returned as {'in'}. This layer accepts a single input only.

Data Types: cell

`NumOutputs` — Number of outputs
`1` (default)

This property is read-only.

Number of outputs from the layer, returned as 1. This layer has a single output only.

Data Types: double

`OutputNames` — Output names
`{'out'}` (default)

This property is read-only.

Output names, returned as {'out'}. This layer has a single output only.

Data Types: cell

Examples

collapse all

Create Convolutional Layer

Open Live Script

Create a convolutional layer with 96 filters, each with a height and width of 11. Use a stride (step size) of 4 in the horizontal and vertical directions.

layer = convolution2dLayer(11,96,'Stride',4)

layer = 
  Convolution2DLayer with properties:

              Name: ''

   Hyperparameters
        FilterSize: [11 11]
       NumChannels: 'auto'
        NumFilters: 96
            Stride: [4 4]
    DilationFactor: [1 1]
       PaddingMode: 'manual'
       PaddingSize: [0 0 0 0]
      PaddingValue: 0

   Learnable Parameters
           Weights: []
              Bias: []

Use properties method to see a list of all properties.

Include a convolutional layer in a Layer array.

layers = [
    imageInputLayer([28 28 1])
    convolution2dLayer(5,20)
    reluLayer
    maxPooling2dLayer(2,'Stride',2)
    fullyConnectedLayer(10)
    softmaxLayer]

layers = 
  6x1 Layer array with layers:

     1   ''   Image Input       28x28x1 images with 'zerocenter' normalization
     2   ''   2-D Convolution   20 5x5 convolutions with stride [1  1] and padding [0  0  0  0]
     3   ''   ReLU              ReLU
     4   ''   2-D Max Pooling   2x2 max pooling with stride [2  2] and padding [0  0  0  0]
     5   ''   Fully Connected   10 fully connected layer
     6   ''   Softmax           softmax

Specify Initial Weights and Biases in Convolutional Layer

Open Live Script

To specify the weights and bias initializer functions, use the WeightsInitializer and BiasInitializer properties respectively. To specify the weights and biases directly, use the Weights and Bias properties respectively.

Specify Initialization Functions

Create a convolutional layer with 32 filters, each with a height and width of 5 and specify the weights initializer to be the He initializer.

filterSize = 5;
numFilters = 32;
layer = convolution2dLayer(filterSize,numFilters, ...
    'WeightsInitializer','he')

layer = 
  Convolution2DLayer with properties:

              Name: ''

   Hyperparameters
        FilterSize: [5 5]
       NumChannels: 'auto'
        NumFilters: 32
            Stride: [1 1]
    DilationFactor: [1 1]
       PaddingMode: 'manual'
       PaddingSize: [0 0 0 0]
      PaddingValue: 0

   Learnable Parameters
           Weights: []
              Bias: []

Use properties method to see a list of all properties.

Note that the Weights and Bias properties are empty. At training time, the software initializes these properties using the specified initialization functions.

Specify Custom Initialization Functions

To specify your own initialization function for the weights and biases, set the WeightsInitializer and BiasInitializer properties to a function handle. For these properties, specify function handles that take the size of the weights and biases as input and output the initialized value.

Create a convolutional layer with 32 filters, each with a height and width of 5 and specify initializers that sample the weights and biases from a Gaussian distribution with a standard deviation of 0.0001.

filterSize = 5;
numFilters = 32;

layer = convolution2dLayer(filterSize,numFilters, ...
    'WeightsInitializer', @(sz) rand(sz) * 0.0001, ...
    'BiasInitializer', @(sz) rand(sz) * 0.0001)

layer = 
  Convolution2DLayer with properties:

              Name: ''

   Hyperparameters
        FilterSize: [5 5]
       NumChannels: 'auto'
        NumFilters: 32
            Stride: [1 1]
    DilationFactor: [1 1]
       PaddingMode: 'manual'
       PaddingSize: [0 0 0 0]
      PaddingValue: 0

   Learnable Parameters
           Weights: []
              Bias: []

Use properties method to see a list of all properties.

Again, the Weights and Bias properties are empty. At training time, the software initializes these properties using the specified initialization functions.

Specify Weights and Bias Directly

Create a fully connected layer with an output size of 10 and set the weights and bias to W and b in the MAT file Conv2dWeights.mat respectively.

filterSize = 5;
numFilters = 32;
load Conv2dWeights

layer = convolution2dLayer(filterSize,numFilters, ...
    'Weights',W, ...
    'Bias',b)

layer = 
  Convolution2DLayer with properties:

              Name: ''

   Hyperparameters
        FilterSize: [5 5]
       NumChannels: 3
        NumFilters: 32
            Stride: [1 1]
    DilationFactor: [1 1]
       PaddingMode: 'manual'
       PaddingSize: [0 0 0 0]
      PaddingValue: 0

   Learnable Parameters
           Weights: [5x5x3x32 double]
              Bias: [1x1x32 double]

Use properties method to see a list of all properties.

Here, the Weights and Bias properties contain the specified values. At training time, if these properties are non-empty, then the software uses the specified values as the initial weights and biases. In this case, the software does not use the initializer functions.

Create Convolutional Layer That Fully Covers Input

Open Live Script

Suppose the size of the input is 28-by-28-by-1. Create a convolutional layer with 16 filters, each with a height of 6 and a width of 4. Set the horizontal and vertical stride to 4.

Make sure the convolution covers the input completely. For the convolution to fully cover the input, both the horizontal and vertical output dimensions must be integer numbers. For the horizontal output dimension to be an integer, one row of padding is required on the top and bottom of the image: (28 – 6+ 2 * 1)/4 + 1 = 7. For the vertical output dimension to be an integer, no zero padding is required: (28 – 4+ 2 * 0)/4 + 1 = 7.

Construct the convolutional layer.

layer = convolution2dLayer([6 4],16,'Stride',4,'Padding',[1 0])

layer = 
  Convolution2DLayer with properties:

              Name: ''

   Hyperparameters
        FilterSize: [6 4]
       NumChannels: 'auto'
        NumFilters: 16
            Stride: [4 4]
    DilationFactor: [1 1]
       PaddingMode: 'manual'
       PaddingSize: [1 1 0 0]
      PaddingValue: 0

   Learnable Parameters
           Weights: []
              Bias: []

Use properties method to see a list of all properties.

Algorithms

expand all

2-D Convolutional Layer

A 2-D convolutional layer applies sliding convolutional filters to 2-D input. The layer convolves the input by moving the filters along the input vertically and horizontally, computing the dot product of the weights and the input, and then adding a bias term.

The dimensions that the layer convolves over depends on the layer input:

For 2-D image input (data with four dimensions corresponding to pixels in two spatial dimensions, the channels, and the observations), the layer convolves over the spatial dimensions.
For 2-D image sequence input (data with five dimensions corresponding to the pixels in two spatial dimensions, the channels, the observations, and the time steps), the layer convolves over the two spatial dimensions.
For 1-D image sequence input (data with four dimensions corresponding to the pixels in one spatial dimension, the channels, the observations, and the time steps), the layer convolves over the spatial and time dimensions.

The convolutional layer consists of various components.¹

Filters and Stride

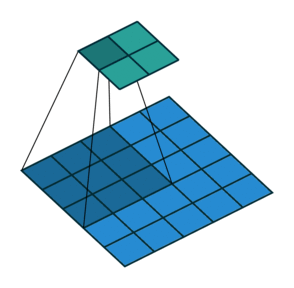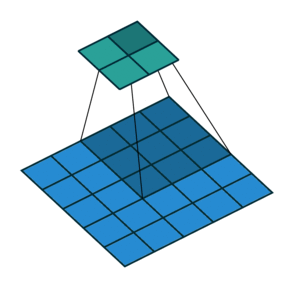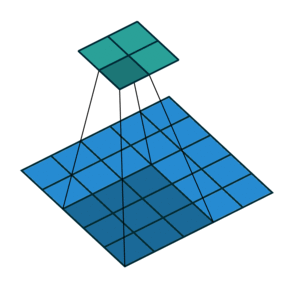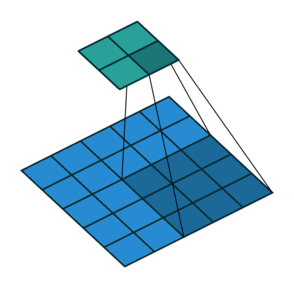
A convolutional layer consists of neurons that connect to subregions of the input images or the outputs of the previous layer. The layer learns the features localized by these regions while scanning through an image. When creating a layer using the convolution2dLayer function, you can specify the size of these regions using the filterSize input argument.

For each region, the layer computes a dot product of the weights and the input, and then adds a bias term. A set of weights that is applied to a region in the image is called a filter. The filter moves along the input image vertically and horizontally, repeating the same computation for each region. In other words, the filter convolves the input.

This image shows a 3-by-3 filter scanning through the input. The lower map represents the input and the upper map represents the output.

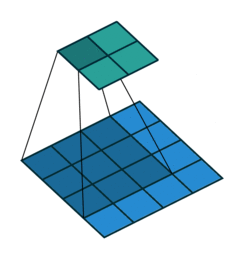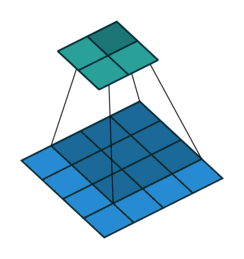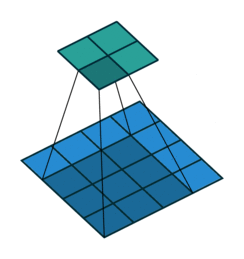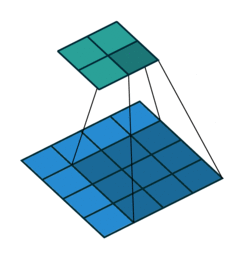
The step size with which the filter moves is called a stride. You can specify the step size with the Stride name-value pair argument. The local regions that the neurons connect to can overlap depending on the filterSize and 'Stride' values.

This image shows a 3-by-3 filter scanning through the input with a stride of 2. The lower map represents the input and the upper map represents the output.

The number of weights in a filter is h * w * c, where h is the height, and w is the width of the filter, respectively, and c is the number of channels in the input. For example, if the input is a color image, the number of color channels is 3. The number of filters determines the number of channels in the output of a convolutional layer. Specify the number of filters using the numFilters argument with the convolution2dLayer function.

Dilated Convolutions

A dilated convolution is a convolution in which the filters are expanded by spaces inserted between the elements of the filter. Specify the dilation factor using the 'DilationFactor' property.

Use dilated convolutions to increase the receptive field (the area of the input which the layer can see) of the layer without increasing the number of parameters or computation.

This image shows a 3-by-3 filter dilated by a factor of two scanning through the input. The lower map represents the input and the upper map represents the output.

Feature Maps

As a filter moves along the input, it uses the same set of weights and the same bias for the convolution, forming a feature map. Each feature map is the result of a convolution using a different set of weights and a different bias. Hence, the number of feature maps is equal to the number of filters. The total number of parameters in a convolutional layer is ((h*w*c + 1)*Number of Filters), where 1 is the bias.

Padding

You can also apply padding to input image borders vertically and horizontally using the 'Padding' name-value pair argument. Padding is values appended to the borders of a the input to increase its size. By adjusting the padding, you can control the output size of the layer.

This image shows a 3-by-3 filter scanning through the input with padding of size 1. The lower map represents the input and the upper map represents the output.

Output Size

The output height and width of a convolutional layer is (Input Size – ((Filter Size – 1)*Dilation Factor + 1) + 2*Padding)/Stride + 1. This value must be an integer for the whole image to be fully covered. If the combination of these options does not lead the image to be fully covered, the software by default ignores the remaining part of the image along the right and bottom edges in the convolution.

Number of Neurons

The product of the output height and width gives the total number of neurons in a feature map, say Map Size. The total number of neurons (output size) in a convolutional layer is Map Size*Number of Filters.

For example, suppose that the input image is a 32-by-32-by-3 color image. For a convolutional layer with eight filters and a filter size of 5-by-5, the number of weights per filter is 5 * 5 * 3 = 75, and the total number of parameters in the layer is (75 + 1) * 8 = 608. If the stride is 2 in each direction and padding of size 2 is specified, then each feature map is 16-by-16. This is because (32 – 5 + 2 * 2)/2 + 1 = 16.5, and some of the outermost padding to the right and bottom of the image is discarded. Finally, the total number of neurons in the layer is 16 * 16 * 8 = 2048.

Usually, the results from these neurons pass through some form of nonlinearity, such as rectified linear units (ReLU).

Learnable Parameters

You can adjust the learning rates and regularization options for the layer using name-value pair arguments while defining the convolutional layer. If you choose not to specify these options, then the trainnet function uses the global training options defined with the trainingOptions function.

Number of Layers

A convolutional neural network can consist of one or multiple convolutional layers. The number of convolutional layers depends on the amount and complexity of the data.

Layer Input and Output Formats

Layers in a layer array or layer graph pass data to subsequent layers as formatted dlarray objects. The format of a dlarray object is a string of characters in which each character describes the corresponding dimension of the data. The formats consist of one or more of these characters:

"S" — Spatial
"C" — Channel
"B" — Batch
"T" — Time
"U" — Unspecified

For example, you can describe 2-D image data that is represented as a 4-D array, where the first two dimensions correspond to the spatial dimensions of the images, the third dimension corresponds to the channels of the images, and the fourth dimension corresponds to the batch dimension, as having the format "SSCB" (spatial, spatial, channel, batch).

You can interact with these dlarray objects in automatic differentiation workflows, such as those for developing a custom layer, using a functionLayer object, or using the forward and predict functions with dlnetwork objects.

This table shows the supported input formats of Convolution2DLayer objects and the corresponding output format. If the software passes the output of the layer to a custom layer that does not inherit from the nnet.layer.Formattable class, or a FunctionLayer object with the Formattable property set to 0 (false), then the layer receives an unformatted dlarray object with dimensions ordered according to the formats in this table. The formats listed here are only a subset. The layer may support additional formats such as formats with additional "S" (spatial) or "U" (unspecified) dimensions.

Input Format	Output Format
`"SSCB"` (spatial, spatial, channel, batch)	`"SSCB"` (spatial, spatial, channel, batch)
`"SCBT"` (spatial, channel, batch, time)	`"SCBT"` (spatial, channel, batch, time)
`"SSCBT"` (spatial, spatial, channel, batch, time)	`"SSCBT"` (spatial, spatial, channel, batch, time)

In dlnetwork objects, Convolution2DLayer objects also support these input and output format combinations.

Input Format	Output Format
`"SSC"` (spatial, spatial, channel)	`"SSCB"` (spatial, spatial, channel)
`"SCT"` (spatial, channel, time)	`"SCBT"` (spatial, channel, time)
`"SSCT"` (spatial, spatial, channel, time)	`"SSCT"` (spatial, spatial, channel, time)

References

[1] LeCun, Y., B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, and L. D. Jackel. "Handwritten Digit Recognition with a Back-Propagation Network." In Advances in Neural Information Processing Systems 2 (D. Touretzky, ed.). San Francisco: Morgan Kaufmann, 1990.

[2] LeCun, Y., L. Bottou, Y. Bengio, and P. Haffner. ''Gradient-Based Learning Applied to Document Recognition.'' Proceedings of the IEEE. Vol. 86, Number 11, 1998, pp. 2278–2324.

[3] Murphy, K. P. Machine Learning: A Probabilistic Perspective. Cambridge, MA: MIT Press, 2012.

[4] Glorot, Xavier, and Yoshua Bengio. "Understanding the Difficulty of Training Deep Feedforward Neural Networks." In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 249–356. Sardinia, Italy: AISTATS, 2010. https://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf

[5] He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. "Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification." In 2015 IEEE International Conference on Computer Vision (ICCV), 1026–34. Santiago, Chile: IEEE, 2015. https://doi.org/10.1109/ICCV.2015.123

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

For code generation, the PaddingValue parameter must be equal to 0, which is the default value.
Code generation does not support passing dlarray objects with unspecified (U) dimensions to this layer.

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Usage notes and limitations:

For code generation, the PaddingValue parameter must be equal to 0, which is the default value.
Code generation does not support passing dlarray objects with unspecified (U) dimensions to this layer.

Version History

Introduced in R2016a

expand all

R2019a: Default weights initialization is Glorot

Starting in R2019a, the software, by default, initializes the layer weights of this layer using the Glorot initializer. This behavior helps stabilize training and usually reduces the training time of deep networks.

In previous releases, the software, by default, initializes the layer weights by sampling from a normal distribution with zero mean and variance 0.01. To reproduce this behavior, set the 'WeightsInitializer' option of the layer to 'narrow-normal'.

convolution2dLayer

Description

Creation

Syntax

Description

Input Arguments

filterSize — Height and width of filters vector of two positive integers | positive integer

numFilters — Number of filters positive integer

Stride — Step size for traversing input [1 1] (default) | vector of two positive integers | positive integer

DilationFactor — Factor for dilated convolution [1 1] (default) | vector of two positive integers | positive integer

Padding — Input edge padding [0 0 0 0] (default) | vector of nonnegative integers | "same"

PaddingValue — Value to pad data 0 (default) | scalar | "symmetric-include-edge" | "symmetric-exclude-edge" | "replicate"

NumChannels — Number of input channels "auto" (default) | positive integer

WeightsInitializer — Function to initialize weights "glorot" (default) | "he" | "narrow-normal" | "zeros" | "ones" | function handle

BiasInitializer — Function to initialize biases "zeros" (default) | "narrow-normal" | "ones" | function handle

Weights — Layer weights [] (default) | numeric array

Bias — Layer biases [] (default) | numeric array

WeightLearnRateFactor — Learning rate factor for weights 1 (default) | nonnegative scalar

BiasLearnRateFactor — Learning rate factor for biases 1 (default) | nonnegative scalar

WeightL2Factor — L2 regularization factor for weights 1 (default) | nonnegative scalar

BiasL2Factor — L2 regularization factor for biases 0 (default) | nonnegative scalar

Name — Layer name "" (default) | character vector | string scalar

Properties

2-D Convolution

FilterSize — Height and width of filters vector of two positive integers

NumFilters — Number of filters positive integer

Stride — Step size for traversing input [1 1] (default) | vector of two positive integers

DilationFactor — Factor for dilated convolution [1 1] (default) | vector of two positive integers

PaddingSize — Size of padding [0 0 0 0] (default) | vector of four nonnegative integers

PaddingMode — Method to determine padding size "manual" (default) | "same"

Padding — Size of padding [0 0] (default) | vector of two nonnegative integers

PaddingValue — Value to pad data 0 (default) | scalar | "symmetric-include-edge" | "symmetric-exclude-edge" | "replicate"

NumChannels — Number of input channels "auto" (default) | positive integer

Parameters and Initialization

WeightsInitializer — Function to initialize weights "glorot" (default) | "he" | "narrow-normal" | "zeros" | "ones" | function handle

BiasInitializer — Function to initialize biases "zeros" (default) | "narrow-normal" | "ones" | function handle

Weights — Layer weights [] (default) | numeric array

Bias — Layer biases [] (default) | numeric array

Learning Rate and Regularization

WeightLearnRateFactor — Learning rate factor for weights 1 (default) | nonnegative scalar

BiasLearnRateFactor — Learning rate factor for biases 1 (default) | nonnegative scalar

WeightL2Factor — L2 regularization factor for weights 1 (default) | nonnegative scalar

BiasL2Factor — L2 regularization factor for biases 0 (default) | nonnegative scalar

Layer

Name — Layer name "" (default) | character vector | string scalar

NumInputs — Number of inputs 1 (default)

InputNames — Input names {'in'} (default)

NumOutputs — Number of outputs 1 (default)

OutputNames — Output names {'out'} (default)

Examples

Create Convolutional Layer

Specify Initial Weights and Biases in Convolutional Layer

Create Convolutional Layer That Fully Covers Input

Algorithms

2-D Convolutional Layer

Layer Input and Output Formats

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.

Version History

R2019a: Default weights initialization is Glorot

See Also

Topics

`filterSize` — Height and width of filters
vector of two positive integers | positive integer

`numFilters` — Number of filters
positive integer

`Stride` — Step size for traversing input
`[1 1]` (default) | vector of two positive integers | positive integer

`DilationFactor` — Factor for dilated convolution
`[1 1]` (default) | vector of two positive integers | positive integer

`Padding` — Input edge padding
`[0 0 0 0]` (default) | vector of nonnegative integers | `"same"`

`PaddingValue` — Value to pad data
0 (default) | scalar | `"symmetric-include-edge"` | `"symmetric-exclude-edge"` | `"replicate"`

`NumChannels` — Number of input channels
`"auto"` (default) | positive integer

`WeightsInitializer` — Function to initialize weights
`"glorot"` (default) | `"he"` | `"narrow-normal"` | `"zeros"` | `"ones"` | function handle

`BiasInitializer` — Function to initialize biases
`"zeros"` (default) | `"narrow-normal"` | `"ones"` | function handle

`Weights` — Layer weights
`[]` (default) | numeric array

`Bias` — Layer biases
`[]` (default) | numeric array

`WeightLearnRateFactor` — Learning rate factor for weights
`1` (default) | nonnegative scalar

`BiasLearnRateFactor` — Learning rate factor for biases
`1` (default) | nonnegative scalar

`WeightL2Factor` — L₂ regularization factor for weights
1 (default) | nonnegative scalar

`BiasL2Factor` — L₂ regularization factor for biases
`0` (default) | nonnegative scalar

`Name` — Layer name
`""` (default) | character vector | string scalar

`FilterSize` — Height and width of filters
vector of two positive integers

`NumFilters` — Number of filters
positive integer

`Stride` — Step size for traversing input
`[1 1]` (default) | vector of two positive integers

`DilationFactor` — Factor for dilated convolution
`[1 1]` (default) | vector of two positive integers

`PaddingSize` — Size of padding
`[0 0 0 0]` (default) | vector of four nonnegative integers

`PaddingMode` — Method to determine padding size
`"manual"` (default) | `"same"`

`Padding` — Size of padding
`[0 0]` (default) | vector of two nonnegative integers

`PaddingValue` — Value to pad data
0 (default) | scalar | `"symmetric-include-edge"` | `"symmetric-exclude-edge"` | `"replicate"`

`NumChannels` — Number of input channels
`"auto"` (default) | positive integer

`WeightsInitializer` — Function to initialize weights
`"glorot"` (default) | `"he"` | `"narrow-normal"` | `"zeros"` | `"ones"` | function handle

`BiasInitializer` — Function to initialize biases
`"zeros"` (default) | `"narrow-normal"` | `"ones"` | function handle

`Weights` — Layer weights
`[]` (default) | numeric array

`Bias` — Layer biases
`[]` (default) | numeric array

`WeightLearnRateFactor` — Learning rate factor for weights
`1` (default) | nonnegative scalar

`BiasLearnRateFactor` — Learning rate factor for biases
`1` (default) | nonnegative scalar

`WeightL2Factor` — L₂ regularization factor for weights
1 (default) | nonnegative scalar

`BiasL2Factor` — L₂ regularization factor for biases
`0` (default) | nonnegative scalar

`Name` — Layer name
`""` (default) | character vector | string scalar

`NumInputs` — Number of inputs
`1` (default)

`InputNames` — Input names
`{'in'}` (default)

`NumOutputs` — Number of outputs
`1` (default)

`OutputNames` — Output names
`{'out'}` (default)

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.