Metrics for System Assessment | Autonomous Navigation, Part 6

Earlier in this series we talked about the capabilities necessary for an autonomous navigation system. We have to sense the environment and then use those measurements to build a map, localize within the map, and model and track the local dynamic objects. Then we have to plan a path to the goal, and finally, act on that plan.

And over the last few videos, we covered conceptually what it means to do localization, mapping, path planning, and tracking. And now that we understand the overall system, in this video, we're going to talk about the different kinds of metrics that we can use to characterize the autonomous navigation system. I hope you stick around for it. I'm Brian, and welcome to a MATLAB Tech Talk.

We want the autonomous navigation system to work, right? But what exactly does that mean? Because working isn't just autonomously reaching a goal in a bunch of different environment conditions, but also doing so safely, robustly-- and if people have to interact with it, then comfortably and predictably-- among other adverbs. But this is where metrics can be useful.

We can transform these vague ideas into something we can measure, something that we can verify through test or simulation, or at the very least, something that we can use as a benchmark to compare to other algorithms and approaches. But as we've seen, autonomous navigation isn't just one algorithm or one component, but a collection of algorithms and components. And so not only does each individual component need to work, but they also have to work together, end to end, to satisfy a larger goal or objective. So ultimately, like any complex engineering project, this is a systems engineering problem.

Let me take a quick detour to talk about systems engineering. Wait-- wait, wait, wait. Please don't leave. I promise this will be fast.

Part of systems engineering is concerned with taking a complex system and breaking it down into smaller and smaller components until you have some level of detail that can be designed and implemented. And each level is defined by a set of requirements or specifications that it must accomplish in order to meet the needs of the higher level system. And then once you have a sufficiently defined set of low level components, you start implementing the design and building it up.

Components build into subsystems. Subsystems built into the system. And at each level, you're verifying that the implementation meets the requirements that were specified during the definition process.

This is the so-called systems engineering V-model-- at least, a very fast introduction to it. But it directly applies to our autonomous navigation problem. Here the top level system might be an autonomous car, and autonomous navigation is one of many subsystems.

And within autonomous navigation, we already know that we've broken it down into sense, mapping, localization, path planning, tracking, and acting. So our job currently as systems engineers is to think about what we want the overall navigation system to do, and then specify what each of these capabilities need to accomplish in order for that to happen. This, again, is where metrics can play an important role, because they provide an objective characterisation of the system or component.

To illustrate some of the metrics that might concern you within autonomous navigation, let's look at a few ways to specify the path planning component. We ask ourselves, what characteristics do we want the path planning algorithm to have? And as an example, let's look at planning a path through a parking lot.

Clearly we want an algorithm that can actually generate a path to the goal if it's reachable and avoids any of the existing obstacles in the environment. That's its main purpose. This is the idea of completeness, which in some cases can be determined algorithmically.

However, just finding a solution might not be sufficient in all scenarios. We may desire specific characteristics for the algorithm. For example, we may put limits on how much memory the algorithm can use or the time it takes to find a solution.

But in addition to the algorithm, we also care about the characteristics of the resulting path. For example, we may want a distance optimal path, or at least, close to the optimal solution given constraints on compute capabilities. In a simulation, we could compare the planned path against an optimal path and calculate metrics like the standard deviation between the two, or the percentage increase in path length. And we could set upper bounds on both of these.

Now for passenger comfort, we may require that the path is sufficiently smooth. You know, it wouldn't be a great ride if your autonomous car instantly jerked to the left. So we could assign smoothness values based on how much the path deviates from a straight line over some specified interval.

The larger this metric, the less smooth the ride would be. And if the returned path doesn't meet the smoothness specification, we may have to re-plan in hopes of finding a smoother solution. Or we might just have to change the algorithm altogether.

Now even if the path is smooth, and it reaches the goal, it might not be good if it passes within a few inches of another car or some other obstacle. It could be scary for both the occupant and the outside observers. Therefore, we may also specify a minimum clearance. And one way to guarantee clearance is to use an inflated representation of the obstacles, when planning.

The resulting path, if we look at it in the original map, now clears the obstacles by at least the amount of the inflation. And there's tons of other metrics that we may want to define and verify as well. But for now, let's move beyond path planning, and look quickly at possible metrics for tracking algorithms.

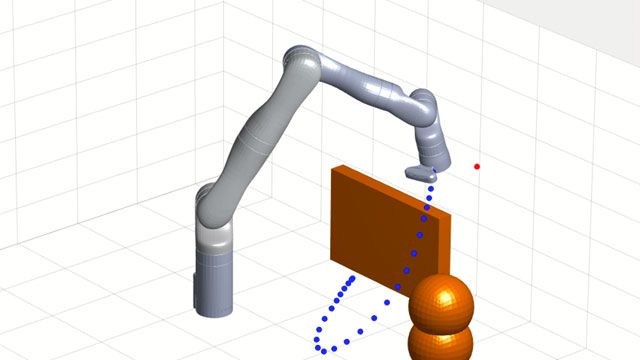
To begin, I want to present two hypothetical tracking situations. In the first, let's say there are two real targets within the local environment that we should be tracking. I'll mark them as Xs on this 2D plane.

One tracking algorithm comes back with three estimated target tracks, indicated with circles. And if we knew the true state of the targets-- that's the Xs, which we could get from a simulation-- then we could determine that this target is being tracked with some amount of error.

This target was missed since there is no estimates within the distance, c, of it. And c, by the way, is called the cut off distance. It's a tunable parameter that you can set to indicate how far away an estimated track would have to be from a true track before you would claim that they are not of the same object.

OK, and then these other two estimated tracks are false tracks, since there are no true targets within a distance, c, of them. In the second example, the true targets are the same, but this time a tracking algorithm returns these two estimated tracks. Here there are no false or miss tracks, and the localization error is smaller for the tracked objects.

So we can look at these two situations and pretty easily claim that the tracking algorithm on the right is doing a much better job than the one on the left. And a better job here is defined as lower localization error and fewer missed and false tracks. And so we could develop three different metrics, one for localization error, one for missed tracks, and one for false tracks. However, it could be useful to roll all of them up into a single metric, a single number that gives us an indication of the similarity between the ground truth and the estimated target set, with a higher number indicating larger deviation between estimation and truth.

Wit a single number, we can use it to set a requirement and then very quickly get a pass/fail result on thousands of simulated test cases. And this would allow us to immediately see how the tracking algorithm performs across a large number of scenarios. Plus, this metric could be generated at each time step, giving us a time history of the quote, "goodness," of the tracking algorithm.

Now capturing localization error and missed and false tracks into a single number is the idea behind OSPA, the optimal sub-pattern assignment metric, and a generalized version of it, called GOSPA. Now the details of these algorithms and why you may choose one over the other can be found in the references that I linked to in the description of this video. But here is a very basic introduction to GOSPA.

Informally, GOSPA can be defined as the sum of the localization errors for the targets that were detected plus a penalty of one half of the cutoff distance for every missed and false track. This is what GOSPA reduces to for parameters alpha equals 2 and p equals 1, which aren't important in this video, but the reference in the description explains all of it.

Now the bottom line is that by describing missed and false tracks as a distance error, there are ways to combine them with localization distance error and arrive at a single metric that we can use to assess tracking performance or to set a requirement for the tracking system. Now again, there's plenty of other metrics that we would want to look at for a tracking system, for example, like how long it takes to establish a new track when an object enters the local environment, or how long it takes to delete a track when an object leaves. And just like with everything I'm talking about here, I've left some resources where you can find more information on tracking metrics. There's always more information.

Now, developing metrics for a component like this is similar to developing metrics for the autonomous navigation system as a whole. We would start by thinking about what we want the system to accomplish, under what environment conditions. How robust does it need to be? How safe? And so on.

And then we need to figure out metrics that we can use to define, or characterize, that desired behavior. These might be really similar to the metrics that you measured at a lower level, but are confirming once again at the system level with all of the other components interacting with each other. For one possible example of this, we talked about how the generated path should have a minimum clearance to obstacles. However, this doesn't mean that the vehicle won't actually get closer than this to the obstacle. Because once you put the whole system together, there are errors in the tracking algorithm and in the mapping algorithm, so you don't quite know what the environment looks like.

And there's also errors in localization, so you don't quite know where you are within the environment. And there are errors in the control system that's trying to get the vehicle to follow that path. And all of these contribute to the overall minimum clearance that the vehicle will experience in the real environment.

Now if the definition of the system was done correctly-- that's this left side of the V-- then we would have an overall minimum clearance requirement at the system level. And the requirements on all of these components would be set such that when they're all combined into the whole system, the high level requirement is met. And so when we run a test, or run a simulation, we would verify each of the components meet their requirements, and then verify that the system meets its requirements.

All right, before I end this video, I want to touch briefly on how we can go about verifying a requirement or calculating a particular metric. For instance, to verify system level minimum clearance we could deploy the software to the vehicle, let it loose in a real environment, and measure how close it gets to obstacles. And then fail it if it gets too close. And running a real test like this is absolutely necessary. However, a simulation might be preferred in a lot of situations, especially in the early stages of verifying a system, because verification often requires a Monte Carlo approach with thousands of simulations that take into account variations in sensor noise and process noise and environment complexities, and all of the different scenarios that the system must operate within.

Now it might be obvious why simulations are preferred over physical tests here, but let me enumerate some reasons. One, it's often easier to control the environment in a simulation, so you can guarantee that you're analyzing your system in the conditions and with the inputs that you want. Two, typically simulations are faster and cheaper than hardware tests, and you can run a lot more of them. And three, you can often get more diagnostic information from a simulation than you can from a physical test. For example, in a simulation, you can know the true state of the system, or the object that's being tracked, and then compare that against what the navigation system claims.

However, with that being said, it's not a good idea to do everything in simulation and then claim that your autonomous navigation system works. This is because a simulated environment will have errors which cause it to deviate from the real environment. For instance, there are errors that come from having to model physical properties that you're not 100% confident in, or from unmodeled, real dynamics that are important to the system. Or just from the fact that there are limitations when modeling continuous dynamics on a digital computer, as well as many, many other sources of error.

And these errors could give you the false sense that your algorithm or component is working correctly. But all you really know is that it works in the simulated environment with the simulated hardware. So a typical approach, especially for model based design, where we've spent a lot of time building a high fidelity model-- one that we have pretty good confidence in-- is to use simulation to verify the system, or just a component of it, over a wide range of conditions, more than what you could possibly test physically. And then confirm that your model is sufficient and that the integrated hardware and software meets the design intent by testing just a subset of the conditions in the real world.

At this point you can compare the output from those physical tests to what your model produced. And if the differences are small or are expected, then you have more confidence in your results from the simulation. Otherwise, you go back and you update your model, and you rerun those conditions again.

All right, so that's where I'm going to leave this for now. Hopefully this video has provided a quick insight into characterizing autonomous navigation systems. And if it has piqued your interest in learning more, please check out all of the references that I've linked to as well as the MATLAB examples that demonstrate some of this in action.

And if you don't want to miss any other future Tech Talk videos, don't forget to subscribe to this channel. And if you want to check out my channel, Control System Lectures, I cover more control theory topics there as well. Thanks for watching, and I'll see you next time.