initial

系统对状态空间模型的初始状态的响应

全页折叠

语法

[y,tOut] = initial(sys,IC)

[y,tOut] = initial(sys,IC,t)

[y,tOut] = initial(sys,IC,t,p)

[y,tOut,x] = initial(___)

[y,tOut,x,pOut] = initial(sys,IC,t,p)

initial(___)

说明

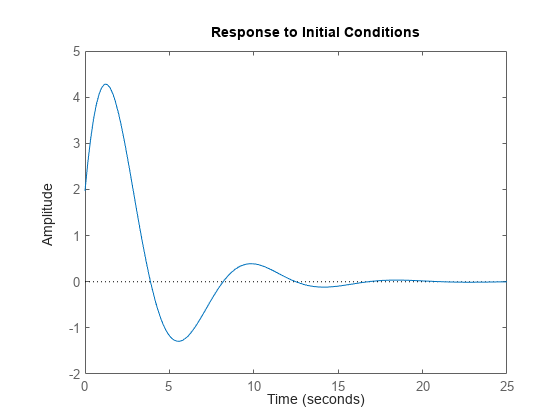
对于状态空间和稀疏状态空间模型，initial 计算系统对初始状态 x_init 的非强迫响应 y。

连续时间：
$\begin{matrix} \dot{x} = d x_{0} + A (x - x_{0}), & x (t_{0}) = x_{i n i t} \\ y = y_{0} + C (x - x_{0}) \end{matrix}$
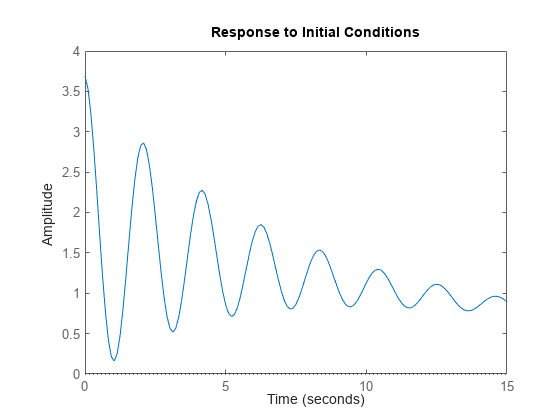
离散时间：
$\begin{matrix} x [k + 1] = d x_{0} + A (x [k] - x_{0}) & x [k_{0}] = x_{i n i t} \\ y = y_{0} + C (x [k] - x_{0}) \end{matrix}$

这是当 u(t) 保持在偏移值 u₀ 时的系统响应。

对于线性时变或线性参数变化状态空间模型，initial 计算具有初始状态 x_init、初始参数 p_init（LPV 模型）且输入保持为偏移值（u(t) = u₀(t) 或 u(t) = u₀(t,p)）时的响应，这对应于局部线性动态特性的初始条件响应。

[y,tOut] = initial(sys,IC) 计算从初始条件 IC 开始的动态系统 sys 的非强迫初始响应 y。时间向量 tOut 采用 sys 的时间单位。initial 根据系统动态特性自动确定仿真的时间步和持续时间。

[y,tOut] = initial(sys,IC,t) 按 t 指定的时间步对响应进行仿真。要定义时间步，您可以：

使用标量值指定最终仿真时间。
使用二元素向量指定初始仿真时间和最终仿真时间。 (自 R2023b 起)
使用向量指定所有时间步。

示例

[y,tOut] = initial(sys,IC,t,p) 指定 LPV 模型的参数轨迹 p。 (自 R2023a 起)

示例

[y,tOut,x] = initial(___) 返回状态轨迹 x。

示例

当 sys 是 LPV 模型时，[y,tOut,x,pOut] = initial(sys,IC,t,p) 返回参数轨迹 pOut。 (自 R2023a 起)

initial(___) 使用所有先前输入参量组合的默认绘图选项绘制 sys 的初始条件响应。如需更多绘图自定义选项，请使用 initialplot。

要在同一图上绘制多个动态系统的响应，您可以将 sys 指定为以逗号分隔的模型列表。例如，initial(sys1,sys2,sys3) 在同一图上绘制三个模型的响应。
要为图中的每个系统分别指定一种颜色、线型和标记，请为每个系统指定 LineSpec 值。例如，initial(sys1,LineSpec1,sys2,LineSpec2) 绘制两个模型并指定它们的绘图样式。有关指定 LineSpec 值的详细信息，请参阅 initialplot。

示例

全部折叠

初始条件响应图

打开实时脚本

对于此示例，生成一个具有 5 个状态的随机状态空间模型，并创建初始状态系统响应图。

rng("default")
sys = rss(5);
x0 = [1,2,3,4,5];
initial(sys,x0)

MATLAB figure

状态空间模型对初始条件的响应

打开实时脚本

绘制以下状态空间模型的响应：

$\begin{array}{rcl} [\begin{array}{l} {x_{}^{˙}}_{1} \\ {x_{}^{˙}}_{2} \end{array}] & = & [\begin{array}{cccccccccccccccccccc} - 0.5572 & - 0.7814 \\ 0.7814 & 0 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}] \\ y & = & [\begin{array}{cccccccccccccccccccc} 1.9691 & 6.4493 \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \end{array}] . \end{array}$

采用以下初始条件：

$x (0) = [\begin{array}{l} 1 \\ 0 \end{array}] .$

a = [-0.5572, -0.7814; 0.7814, 0];
c = [1.9691  6.4493];
x0 = [1 ; 0];

sys = ss(a,[],c,[]);
initial(sys,x0)

MATLAB figure

MIMO 系统的初始条件响应图

打开实时脚本

假设有以下双输入、双输出动态系统。

$s y s (s) = [\begin{array}{cccccccccccccccccccc} 0 & \frac{3 s}{s^{2} + s + 10} \\ \frac{s + 1}{s + 5} & \frac{2}{s + 6} \end{array}] .$

将 sys 转换为状态空间形式，因为初始条件响应图仅支持状态空间模型。

sys = ss([0, tf([3 0],[1 1 10]) ; tf([1 1],[1 5]), tf(2,[1 6])]);
size(sys)

State-space model with 2 outputs, 2 inputs, and 4 states.

得到的状态空间模型有四个状态。因此，提供一个具有四个元素的初始条件向量。

x0 = [0.3,0.25,1,4];

创建初始条件响应图。

initial(sys,x0);

MATLAB figure

得到的图包含两个子图 - sys 中的每个输出各对应一个子图。

指定时间时的初始条件响应图

打开实时脚本

对于此示例，检查以下零极点增益模型的初始条件响应，并将绘图限制在 tFinal = 15 秒。

首先，将 zpk 模型转换为 ss 模型，因为 initial 仅支持状态空间模型。

sys = ss(zpk(-1,[-0.2+3j,-0.2-3j],1)*tf([1 1],[1 0.05]));
tFinal = 15;
x0 = [4,2,3];

现在，创建初始条件响应图。

initial(sys,x0,tFinal);

MATLAB figure

多个系统的初始条件响应

打开实时脚本

对于此示例，绘制三个动态系统的初始条件响应。

首先，创建这三个模型并提供初始条件。所有模型的状态数应相同。

rng('default');
sys1 = rss(4); 
sys2 = rss(4);
sys3 = rss(4);
x0 = [1,1,1,1];

使用跨度为 5 秒的时间向量 t 绘制这三个模型的初始条件响应。

t = 0:0.1:5;
initial(sys1,'r--',sys2,'b',sys3,'g-.',x0,t)

MATLAB figure

状态空间模型的初始条件响应数据

打开实时脚本

提取以下具有两个状态的状态空间模型的初始条件响应数据：

使用以下初始条件：

$x (0) = [\begin{array}{l} 1 \\ 0 \end{array}] .$

a = [-0.5572, -0.7814; 0.7814, 0];
c = [1.9691  6.4493];
x0 = [1 ; 0];
sys = ss(a,[],c,[]);
[y,tOut,x] = initial(sys,x0);

数组 y 的行数与时间采样数相同（tOut 的长度）相同，列数与输出数相同。类似地，x 的行数等于时间采样数（tOut 的长度），列数与输出数相同。

指定时间的初始条件响应数据

打开实时脚本

对于此示例，提取具有 6 个状态、3 个输出和 2 个输入的状态空间模型的初始条件响应数据。

首先，创建该模型并提供初始条件。

rng('default');
sys = rss(6,3,2); 
x0 = [0.1,0.3,0.05,0.4,0.75,1];

使用跨度为 15 秒的时间向量 t 提取该模型的初始条件响应。

t = 0:0.1:15;
[y,tOut,x] = initial(sys,x0,t);

数组 y 的行数与时间采样数相同（tOut 的长度）相同，列数与输出数相同。类似地，x 的行数等于时间采样数（tOut 的长度），列数与输出数相同。

线性参数变化状态空间模型的初始响应

打开实时脚本

对于此示例，throttleLPV.m 定义了一个非线性发动机节气门的动态特性，该节气门在 15 度到 90 度的开度范围内呈线性行为。

使用 lpvss 创建此模型。此模型由节气门角度进行参数化，节气门角度是此模型的第一个状态。

c0 = 50;
k0 = 120;
K0 = 1e4;
b0 = 4e4;
yf = 15*K0/(k0+K0);
Ts = 0;
sys = lpvss("x1",@(t,p) throttleLPV(p,c0,k0,b0,K0),Ts,0,15);

您可以沿轨迹 $p (t)$ 计算此模型的初始响应。

计算从线性范围的下限以较小的角速度开始条件下的响应。指定参数轨迹，并使用 findop 找到初始条件。

pFcn = @(t,x,u)x(1);
xinit = [15;10]; 
pinit = xinit(1);
t = linspace(0,0.6,500);
ic = findop(sys,t(1),pinit,x=xinit);
y = initial(sys,ic,t,pFcn);
plot(t,y)

Figure contains an axes object. The axes object contains an object of type line.

计算从线性范围的下限以足够大的角速度开始以达到该范围的上限条件下的响应。

xinit2 = [15;5e3]; 
pinit2 = xinit2(1);
t2 = linspace(0,1,1000);
ic2 = findop(sys,t2(1),pinit2,x=xinit2);
y2 = initial(sys,ic2,t2,pFcn);
plot(t2,y2)

Figure contains an axes object. The axes object contains an object of type line.

查看数据函数。

type throttleLPV.m

function [A,B,C,D,E,dx0,x0,u0,y0,Delays] = throttleLPV(x1,c,k,b,K)
% LPV representation of engine throttle dynamics.
% Ref: https://www.mathworks.com/help/sldo/ug/estimate-model-parameter-values-gui.html
% x1: scheduling parameter (throttle angle; first state of the model)
% c,k,b,K: physical parameters

A = [0 1; -k -c];
B = [0; b];
C = [1 0];
D = 0;
E = [];
Delays = [];
x0 = [];
u0 = [];
y0 = [];

% Nonlinear displacement value
NLx = max(90,x1(1))-90+min(x1(1),15)-15;
% Capture the nonlinear contribution as a state-derivative offset
dx0 = [0;-K*NLx];

计算具有复系数的模型的初始条件响应

打开实时脚本

创建一个具有复系数的状态空间模型。

A = [-2-2i -2;1 0];
B = [2;0];
C = [0 0.5+2.5i];
D = 0;
sys = ss(A,B,C,D);

计算该系统对任意起始状态的初始条件响应。

ic = [1 2];
[y,t] = initial(sys,ic);

得到的响应数据包含复数输出值。

y = 334×1 complex

   1.0000 + 5.0000i
   1.0301 + 5.1157i
   1.0607 + 5.1854i
   1.0868 + 5.2140i
   1.1047 + 5.2062i
   1.1116 + 5.1670i
   1.1056 + 5.1012i
   1.0854 + 5.0135i
   1.0506 + 4.9082i
   1.0014 + 4.7894i
   0.9383 + 4.6608i
   0.8623 + 4.5255i
   0.7747 + 4.3864i
   0.6769 + 4.2458i
   0.5706 + 4.1057i
      ⋮

输入参数

全部折叠

`sys` — 动态状态空间模型
动态状态空间模型 | 模型数组

动态系统，指定为 SISO 或 MIMO 动态系统模型或动态系统模型数组。您只能使用以下类型的状态空间模型：

连续时间或离散时间数值 ss 模型。
广义或不确定的 LTI 模型，如 genss 或 uss 模型。（使用不确定模型需要 Robust Control Toolbox™ 软件。）
- 对于可调控制设计模块，该函数在绘图和返回响应数据时，都会根据其当前值评估模型。
- 对于不确定的控制设计模块，该函数绘制模型的标称值和随机样本。使用输出参量时，该函数仅返回标称模型的响应数据。
稀疏状态空间模型，如 sparss 和 mechss 模型。对于稀疏状态空间模型，您必须指定最终时间 tFinal。
线性时变 (ltvss) 和线性参数变化 (lpvss) 模型。

如果 sys 是模型数组，该函数会在同一坐标区中绘制数组中所有模型的响应。

`t` — 时间步
正标量 | 二元素向量 | 向量 | `[]`

要计算响应的时间步，指定为以下值之一：

正标量 tFinal - 计算从 t = 0 到 t = tFinal 的响应。
二元素向量 [t0 tFinal] - 计算从 t = t0 到 t = tFinal 的响应。 (自 R2023b 起)
向量 Ti:dt:Tf - 计算 t 中指定的时间点的响应。
- 对于连续时间系统，dt 是连续系统的离散逼近的采样时间。
- 对于具有指定采样时间的离散时间系统，dt 必须与 sys 的采样时间属性 Ts 匹配。
- 对于未指定采样时间 (Ts = -1) 的离散时间系统，dt 必须为 1。
[] - 根据系统动态特性自动选择时间值。

当您使用 tFinal 或 [t0 tFinal] 指定时间范围时：

对于连续时间系统，该函数根据系统动态特性自动确定步长和点数。
对于具有指定采样时间的离散时间系统，该函数使用 sys 的采样时间作为步长。
对于未指定采样时间 (Ts = -1) 的离散时间系统，该函数将 tFinal 解释为采样时间为 1 秒时要仿真的采样周期数。

使用 sys 的 TimeUnit 属性中指定的时间单位表示 t。

`IC` — 初始条件
向量 | `RespConfig` 对象 | 使用 `findop` 创建的工况

初始条件，指定为以下项之一：

初始状态值，指定为向量 xinit，其长度等于状态数。
响应配置，指定为 RespConfig 对象。使用此对象指定 LPV 模型的初始状态和参数值。 (自 R2024b 起)
工况，指定为使用 findop 创建的对象。 (自 R2024b 起)

`p` — LPV 模型参数轨迹
矩阵 | 函数句柄

自 R2023a 起

LPV 模型的参数轨迹，指定为矩阵或函数句柄。

对于外生轨迹或显式轨迹，将 p 指定为维度为 N×Np 的矩阵，其中 N 是时间采样的数目，Np 是参数的数目。
因此，行向量 p(i,:) 包含第 i 个时间步处的参数值。
对于内生轨迹或隐式轨迹，在连续时间内将 p 指定为 p = F(t,x,u) 形式的函数句柄，在离散时间内将其指定为 p = F(k,x,u) 形式的函数句柄，从而将参数作为时间 t 或时间采样 k、状态 x 和输入 u 的函数提供。此输入方法需要初始参数值。要指定初始条件，请使用 IC 参量。

输出参量

全部折叠

`y` — 响应数据
数组

响应数据，以数组形式返回。

对于 SISO 系统，y 是与 t（如果提供）或 tOut（如果未提供 t）长度相同的列向量。
对于单输入、多输出系统，y 是行数与时间采样数相同、列数与输出数相同的矩阵。因此，y 的第 j 列或 y(:,j) 包含从输入到第 j 个输出的响应。
对于 MIMO 系统，y 的维度为 N×Ny，其中：
- N 是时间采样的数目。
- Ny 是系统输出的数目。
对于具有复系数的系统，y 是复数值数组。 (自 R2025a 起)

`tOut` — 计算响应的时间
向量

计算响应的时间，以向量形式返回。如果您未提供特定的时间向量 t，initial 会根据系统动态特性选择此时间向量。时间以 sys 的时间单位表示。

`x` — 状态轨迹
数组

状态轨迹，以数组形式返回。x 包含 sys 的状态在 t 或 tOut 中的每个时间点的演化。x 的维度为 N×Nx，其中：

N 是时间采样的数目。
Nx 是状态的数目。

对于具有复系数的系统，x 是复数值数组。 (自 R2025a 起)

`pOut` — 参数轨迹
数组

自 R2023a 起

参数轨迹，以数组形式返回。当 sys 是线性参数变化 (lpvss) 模型时，pOut 包含 sys 的参数的演化。pOut 的维度为 N×Np，其中：

N 是时间采样的数目。
Np 是参数的数目。

提示

当您需要额外的绘图自定义选项时，请改用 initialplot。
使用 initial 创建的绘图不支持以字符串数组或字符向量元胞数组形式指定的多行标题或标签。要指定多行标题和标签，请使用包含 newline 字符的单个字符串。
```
initial(sys)
title("first line" + newline + "second line");
```

版本历史记录

在 R2006a 之前推出

全部展开

R2025a: 支持具有复系数的动态系统

从 R2025a 开始，initial 函数支持具有复系数的动态系统。

R2024b: 使用 `findop` 或 `RespConfig` 指定初始条件

现在，您可以使用 RespConfig 和 findop 采用 [y,t] = initial(sys,IC,__) 语法来指定初始条件。有关详细信息，请参阅 IC 输入参量。

由于这一变更，xinit 参量已重命名为 IC。

R2024b: 不推荐使用语法

现在，您可以使用 RespConfig 对象或使用 findop 计算得到的工作点对象来为线性参数变化 (LPV) 模型的状态和参数值提供初始条件。因此，不推荐使用语法 [y,tOut] = initial(sys,{xinit,pinit},t,p)。要更新您的代码，请使用以下推荐的工作流：

`RespConfig`	IC = RespConfig(InitialState=xinit,InitialParameter=pinit); [y,tOut] = initial(sys,IC,t,p);
`findop`	IC = findop(sys,Ti,pinit,x=xinit); [y,tOut] = initial(sys,IC,t,p);

R2024b: `gca` 现在返回图对象

对于使用 initial 创建的绘图，gca 函数现在返回 initialplot 图对象，而不是绘图内的坐标区。

R2023b: 新语法

使用新语法 [y,tOut] = initial(sys,[t0,tFinal]) 计算从时间 t0 到 tFinal 的冲激响应。

另请参阅

initialplot | impulse | lsim | 线性系统分析器 | step

主题

Response from Initial Conditions

initial

语法

说明

示例

初始条件响应图

状态空间模型对初始条件的响应

MIMO 系统的初始条件响应图

指定时间时的初始条件响应图

多个系统的初始条件响应

状态空间模型的初始条件响应数据

指定时间的初始条件响应数据

线性参数变化状态空间模型的初始响应

计算具有复系数的模型的初始条件响应

输入参数

sys — 动态状态空间模型 动态状态空间模型 | 模型数组

t — 时间步 正标量 | 二元素向量 | 向量 | []

IC — 初始条件 向量 | RespConfig 对象 | 使用 findop 创建的工况

p — LPV 模型参数轨迹 矩阵 | 函数句柄

输出参量

y — 响应数据 数组

tOut — 计算响应的时间 向量

x — 状态轨迹 数组

pOut — 参数轨迹 数组

提示

版本历史记录

R2025a: 支持具有复系数的动态系统

R2024b: 使用 findop 或 RespConfig 指定初始条件

R2024b: 不推荐使用语法

R2024b: gca 现在返回图对象

R2023b: 新语法

另请参阅

主题

`sys` — 动态状态空间模型
动态状态空间模型 | 模型数组

`t` — 时间步
正标量 | 二元素向量 | 向量 | `[]`

`IC` — 初始条件
向量 | `RespConfig` 对象 | 使用 `findop` 创建的工况

`p` — LPV 模型参数轨迹
矩阵 | 函数句柄

`y` — 响应数据
数组

`tOut` — 计算响应的时间
向量

`x` — 状态轨迹
数组

`pOut` — 参数轨迹
数组

R2024b: 使用 `findop` 或 `RespConfig` 指定初始条件

R2024b: `gca` 现在返回图对象