Main Content

Closing Feedback Loops with Time Delays

This example shows how internal delays arise when you interconnect models that have input, output, or transport time delays.

Create a model of the following control architecture:

G is the plant model, which has an input delay. C is a proportional-integral (PI) controller.

To create a model representing the closed-loop response of this system:

  1. Create the plant G and the controller C.

    G = tf(1,[1 10],'InputDelay',2.1); 
C = pid(0.5,2.3);

    C has a proportional gain of 0.5 and an integral gain of 2.3.

  2. Use feedback to compute the closed-loop response from r to y.

    T = feedback(C*G,1);

The time delay in T is not an input delay as it is in G. Because the time delay is internal to the closed-loop system, the software returns T as an ss model with an internal time delay of 2.1 seconds.

Note

In addition to feedback, any system interconnection function (including parallel and series) can give rise to internal delays.

T is an exact representation of the closed-loop response, not an approximation. To access the internal delay value, enter:

T.InternalDelay

A step plot of T confirms the presence of the time delay:

step(T)

Note

Most analysis commands, such as step, bode and margin, support models with internal delays.

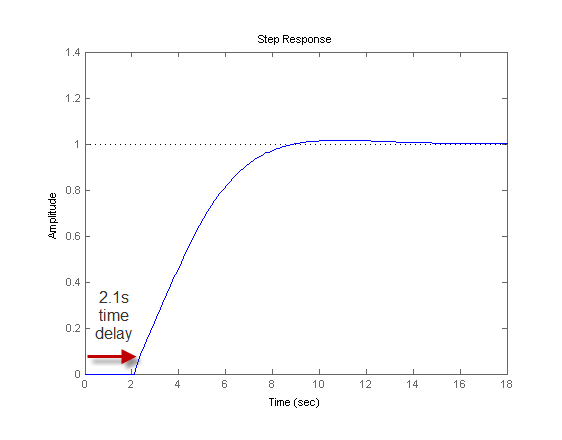
The internal time delay is stored in the InternalDelay property of T. Use dot notation to access InternalDelay. For example, to change the internal delay to 3.5 seconds, enter:

 T.InternalDelay = 3.5

You cannot modify the number of internal delays because they are structural properties of the model.

Related Examples

More About