Create Bidirectional LSTM (BiLSTM) Function

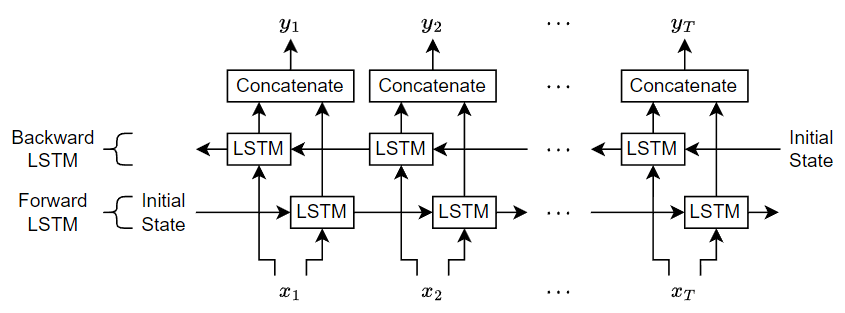
Create BiLSTM Function

Create the bilstm function, listed at the end of the example, that applies a BiLSTM operation to the input using the initial hidden state, initial cell state, and the input weights, recurrent weights, and the bias.

Initialize BiLSTM Parameters

Specify the input size (for example, the embedding dimension of the input layer) and the number of hidden units.

inputSize = 256;
numHiddenUnits = 50;

Initialize the BILSTM parameters. The BiLSTM operation requires a set of input weights, recurrent weights, and bias for both the forward and backward parts of the operation. For these parameters, specify the concatenation of the forward and backward components. In this case, the input weights have size [8*numHiddenUnits inputSize], the recurrent weights have size [8*numHiddenUnits numHiddenUnits], and the bias has size [8*numHiddenUnits 1].

Initialize the input weights, recurrent weights, and the bias using the initializeGlorot, initializeOrthogonal, and initializeUnitForgetGate functions, respectively. These functions are attached to this example as supporting files. To access these functions, open the example as a live script.

Initialize the input weights using the initializeGlorot function.

numOut = 8*numHiddenUnits;
numIn = inputSize;
sz = [numOut numIn];
inputWeights = initializeGlorot(sz,numOut,numIn);

Initialize the recurrent weights using the initializeOrthogonal function.

sz = [8*numHiddenUnits numHiddenUnits];
recurrentWeights = initializeOrthogonal(sz);

Initialize the input weights using the initializeUnitForgetGate function.

bias = initializeUnitForgetGate(2*numHiddenUnits);

Initialize the BiLSTM hidden and cell state with zeros using the initializeZeros function attached to this example as a supporting file. To access this function, open the example as a live script. Similar to the parameters, specify the concatenation of the forward and backward components. In this case, the hidden and cell state each have size [2*numHiddenUnits 1].

sz = [2*numHiddenUnits 1];
H0 = initializeZeros(sz);
C0 = initializeZeros(sz);

Apply BiLSTM Operation

Specify an array of random data with mini-batch size 128 and sequence length 75. The first dimension of the input (the channel dimension) must match the input size of the BiLSTM operation.

miniBatchSize = 128;
sequenceLength = 75;
X = rand([inputSize miniBatchSize sequenceLength],"single");
X = dlarray(X,"CBT");

Apply the BiLSTM operation and view the size of the output.

Y = bilstm(X,H0,C0,inputWeights,recurrentWeights,bias);
size(Y)

ans = 1×3

   100   128    75

For models that require only the last time step of the sequence, extract the vectors corresponding to the last output of the forward LSTM and backward LSTM components.

YLastForward = Y(1:numHiddenUnits,:,end);
YLastBackward = Y(numHiddenUnits+1:end,:,1);

YLast = cat(1, YLastForward, YLastBackward);
size(YLast)

ans = 1×3

   100   128     1

BiLSTM Function

The bilstm function applies a BiLSTM operation to the formatted dlarray input X using the initial hidden state H0, initial cell state C0, and parameters weights, recurrentWeights, and bias. The input weights have size [8*numHiddenUnits inputSize], the recurrent weights have size [8*numHiddenUnits numHiddenUnits], and the bias has size [8*numHiddenUnits 1]. The hidden and cell state each have size [2*numHiddenUnits 1].

function [Y,hiddenState,cellState] = bilstm(X,H0,C0,inputWeights,recurrentWeights,bias)

% Determine forward and backward parameter indices
numHiddenUnits = numel(bias)/8;
idxForward = 1:4*numHiddenUnits;
idxBackward = 4*numHiddenUnits+1:8*numHiddenUnits;

% Forward and backward states
H0Forward = H0(1:numHiddenUnits);
H0Backward = H0(numHiddenUnits+1:end);
C0Forward = C0(1:numHiddenUnits);
C0Backward = C0(numHiddenUnits+1:end);

% Forward and backward parameters
inputWeightsForward = inputWeights(idxForward,:);
inputWeightsBackward = inputWeights(idxBackward,:);
recurrentWeightsForward = recurrentWeights(idxForward,:);
recurrentWeightsBackward = recurrentWeights(idxBackward,:);
biasForward = bias(idxForward);
biasBackward = bias(idxBackward);

% Forward LSTM
[YForward,hiddenStateForward,cellStateForward] = lstm(X,H0Forward,C0Forward,inputWeightsForward, ...
    recurrentWeightsForward,biasForward);

% Backward LSTM
XBackward = X;
idx = finddim(X,"T");
if ~isempty(idx)
    XBackward = flip(XBackward,idx);
end

[YBackward,hiddenStateBackward,cellStateBackward] = lstm(XBackward,H0Backward,C0Backward,inputWeightsBackward, ...
    recurrentWeightsBackward,biasBackward);

if ~isempty(idx)
    YBackward = flip(YBackward,idx);
end

% Output
Y = cat(1,YForward,YBackward);
hiddenState = cat(1,hiddenStateForward,hiddenStateBackward);
cellState = cat(1,cellStateForward,cellStateBackward);

end