使用深度学习进行“序列到序列”回归

此示例说明如何使用深度学习预测发动机的剩余使用寿命 (RUL)。

要训练深度神经网络以根据时间序列数据或序列数据预测数值，可以使用长短期记忆 (LSTM) 网络。

此示例使用 [1] 中所述的涡轮风扇发动机退化仿真数据集。该示例训练一个 LSTM 网络，旨在根据表示发动机中各种传感器的时间序列数据来预测发动机的剩余使用寿命（预测性维护，以周期为单位进行测量）。训练数据包含 100 台发动机的仿真时间序列数据。每个序列的长度各不相同，对应于完整的运行至故障 (RTF) 实例。测试数据包含 100 个不完整序列，每个序列的末尾为相应的剩余使用寿命值。

该数据集包含 100 个训练观测值和 100 个测试观测值。

下载数据

下载并解压缩涡轮风扇发动机退化仿真数据集。

涡轮风扇发动机退化仿真数据集的每个时间序列表示一个发动机。每台发动机启动时的初始磨损程度和制造变差均未知。发动机在每个时间序列开始时运转正常，在到达序列中的某一时刻时出现故障。在训练集中，故障的规模不断增大，直到出现系统故障。

数据是 ZIP 压缩的文本文件，其中包含 26 列以空格分隔的数值。每一行是在一个运转周期中截取的数据快照，每一列代表一个不同的变量。这些列分别对应于以下数据：

第 1 列 - 单元编号
第 2 列 - 周期时间
第 3-5 列 - 操作设置
第 6-26 列 - 传感器测量值 1-21

创建一个目录来存储涡轮风扇发动机退化仿真数据集。

dataFolder = fullfile(tempdir,"turbofan");
if ~exist(dataFolder,"dir")
    mkdir(dataFolder);
end

下载并提取涡轮风扇发动机退化仿真数据集。

filename = matlab.internal.examples.downloadSupportFile("nnet","data/TurbofanEngineDegradationSimulationData.zip");
unzip(filename,dataFolder)

准备训练数据

使用此示例附带的函数 processTurboFanDataTrain 加载数据。函数 processTurboFanDataTrain 从 filenamePredictors 中提取数据并返回元胞数组 XTrain 和 TTrain，其中包含训练预测变量和响应序列。

filenamePredictors = fullfile(dataFolder,"train_FD001.txt");
[XTrain,TTrain] = processTurboFanDataTrain(filenamePredictors);

删除具有常量值的特征

在所有时间步都保持不变的特征可能对训练产生负面影响。找到最小值和最大值相同的数据行，然后删除这些行。

XTrainConcatenatedTimesteps = cat(1,XTrain{:});
m = min(XTrainConcatenatedTimesteps,[],1);
M = max(XTrainConcatenatedTimesteps,[],1);
idxConstant = M == m;

for i = 1:numel(XTrain)
    XTrain{i}(:,idxConstant) = [];
end

查看序列中其余特征的数量。

numFeatures = size(XTrain{1},2)

numFeatures = 17

归一化训练预测变量

将训练预测变量归一化为具有零均值和单位方差。要计算所有观测值的均值和标准差，请水平串联序列数据。

XTrainConcatenatedTimesteps = cat(1,XTrain{:});
mu = mean(XTrainConcatenatedTimesteps,1);
sig = std(XTrainConcatenatedTimesteps,0,1);

for i = 1:numel(XTrain)
    XTrain{i} = (XTrain{i} - mu) ./ sig;
end

裁剪响应

要更多地从发动机快要出现故障时的序列数据中进行学习，请以阈值 150 对响应进行裁剪。这会使网络将具有更高 RUL 值的实例视为等同。

thr = 150;
for i = 1:numel(TTrain)
    TTrain{i}(TTrain{i} > thr) = thr;
end

下图显示了第一个观测值及其对应的裁剪响应。

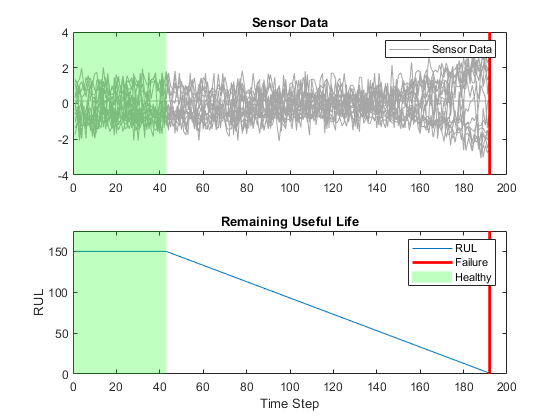
准备要填充的数据

要最大程度地减少添加到小批量的填充量，请按序列长度对训练数据进行排序。然后，选择可均匀划分训练数据的小批量大小，并减少小批量中的填充量。

按序列长度对训练数据进行排序。

for i=1:numel(XTrain)
    sequence = XTrain{i};
    sequenceLengths(i) = size(sequence,1);
end

[sequenceLengths,idx] = sort(sequenceLengths,"descend");
XTrain = XTrain(idx);
TTrain = TTrain(idx);

在条形图中查看排序的序列长度。

figure
bar(sequenceLengths)
xlabel("Sequence")
ylabel("Length")
title("Sorted Data")

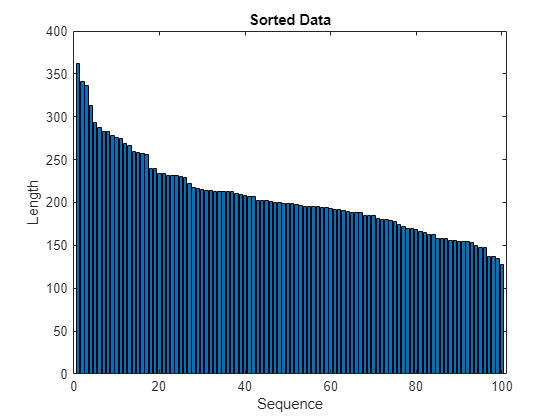
选择可均匀划分训练数据的小批量大小，并减少小批量中的填充量。下图显示了大小为 20 的小批量添加到未排序序列和已排序序列的填充情况。

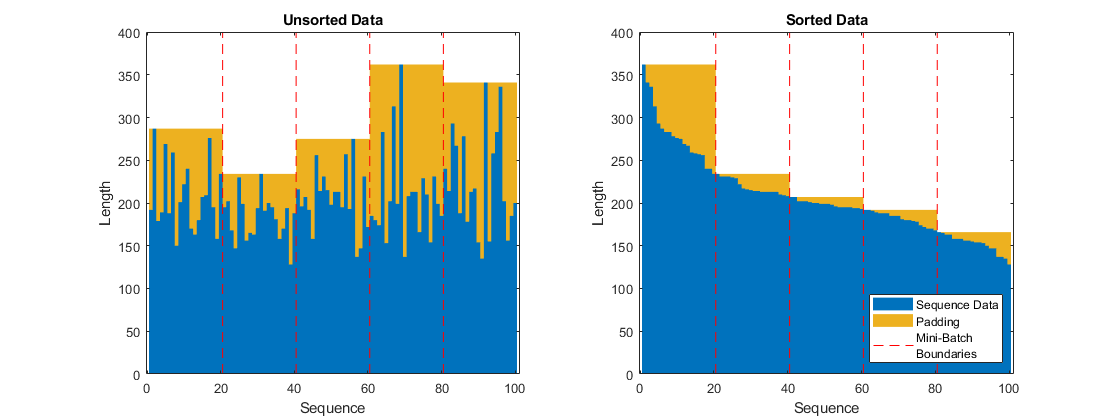
定义网络架构

定义网络架构。创建一个 LSTM 网络，该网络包含一个具有 200 个隐藏单元的 LSTM 层，然后是一个大小为 50 的全连接层和一个丢弃概率为 0.5 的丢弃层。

numResponses = size(TTrain{1},2);
numHiddenUnits = 200;

layers = [ ...
    sequenceInputLayer(numFeatures)
    lstmLayer(numHiddenUnits,OutputMode="sequence")
    fullyConnectedLayer(50)
    dropoutLayer(0.5)
    fullyConnectedLayer(numResponses)];

指定训练选项。使用求解器 "adam" 以大小为 20 的小批量进行 60 轮训练。指定学习率为 0.01。要防止梯度爆炸，请将梯度阈值设置为 1。要使序列保持按长度排序，请将 Shuffle 选项设置为 "never"。在图中显示训练进度并监控均方根误差 (RMSE) 度量。

maxEpochs = 60;
miniBatchSize = 20;

options = trainingOptions("adam", ...
    MaxEpochs=maxEpochs, ...
    MiniBatchSize=miniBatchSize, ...
    InitialLearnRate=0.01, ...
    GradientThreshold=1, ...
    Shuffle="never", ...
    Metrics="rmse", ...
    Plots="training-progress", ...
    Verbose=0);

训练网络

使用 trainnet 函数训练神经网络。对于回归，请使用均方误差损失。默认情况下，trainnet 函数使用 GPU（如果有）。在 GPU 上进行训练需要 Parallel Computing Toolbox™ 许可证和受支持的 GPU 设备。有关受支持设备的信息，请参阅GPU Computing Requirements (Parallel Computing Toolbox)。否则，trainnet 函数使用 CPU。要指定执行环境，请使用 ExecutionEnvironment 训练选项。

net = trainnet(XTrain,TTrain,layers,"mse",options);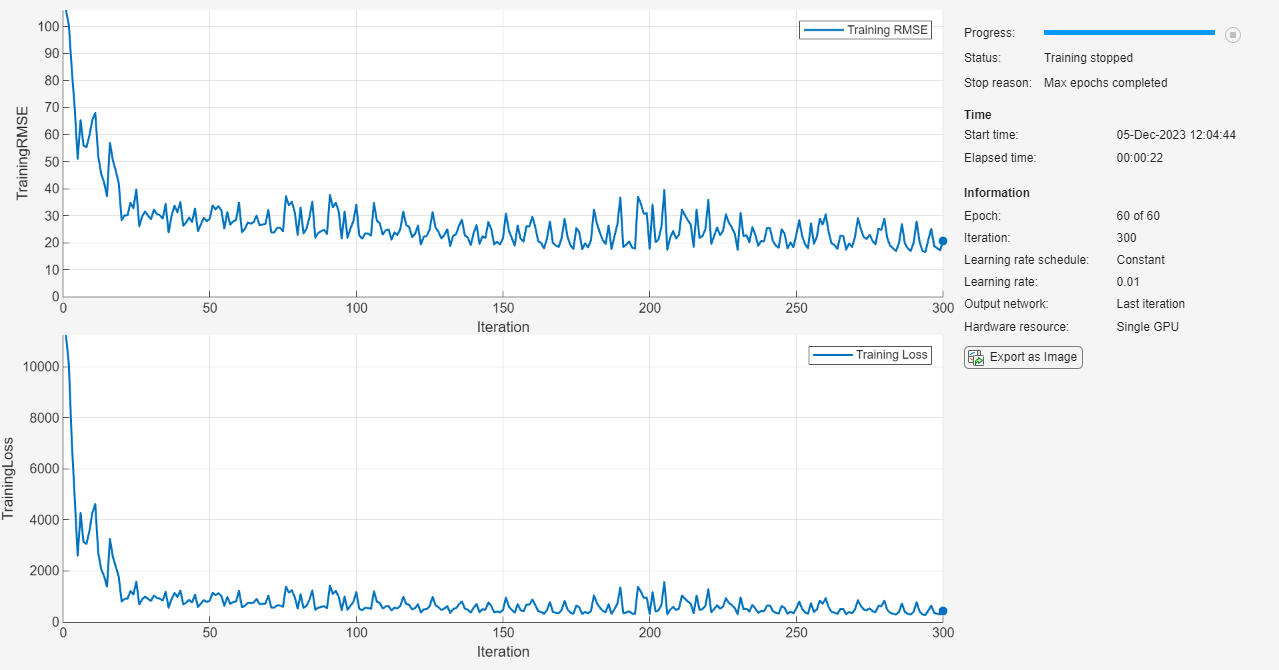

测试网络

使用此示例附带的函数 processTurboFanDataTest 准备测试数据。函数 processTurboFanDataTest 从 filenamePredictors 和 filenameResponses 中提取数据并返回元胞数组 XTest 和 TTest，其中分别包含测试预测变量和响应序列。

filenamePredictors = fullfile(dataFolder,"test_FD001.txt");
filenameResponses = fullfile(dataFolder,"RUL_FD001.txt");
[XTest,TTest] = processTurboFanDataTest(filenamePredictors,filenameResponses);

使用根据训练数据计算出的 idxConstant 删除具有常量值的特征。使用与训练数据相同的参数来归一化测试预测变量。使用与训练数据相同的阈值对测试响应进行裁剪。

for i = 1:numel(XTest)
    XTest{i}(:,idxConstant) = [];
    XTest{i} = (XTest{i} - mu) ./ sig;
    TTest{i}(TTest{i} > thr) = thr;
end

使用神经网络进行预测。要使用多个观测值进行预测，请使用 minibatchpredict 函数。minibatchpredict 函数自动使用 GPU（如果有）。使用 GPU 需要 Parallel Computing Toolbox™ 许可证和受支持的 GPU 设备。有关受支持设备的信息，请参阅 GPU 计算要求。否则，该函数使用 CPU。为防止函数向数据添加填充，请指定小批量大小为 1。要在元胞数组中返回预测值，请将 UniformOutput 设置为 false。

YTest = minibatchpredict(net,XTest,MiniBatchSize=1,UniformOutput=false);

LSTM 网络对不完整序列进行预测，一次预测一个时间步。在每个时间步，网络使用此时间步的值进行预测，网络状态仅根据先前的时间步进行计算。网络在各次预测之间更新其状态。minibatchpredict 函数返回这些预测值的序列。预测值的最后一个元素对应于不完整序列的预测 RUL。

您也可以使用 predict 一次对一个时间步进行预测，并更新网络 State 属性。这在时间步的值以流的方式到达时非常有用。通常，对完整序列进行预测比一次对一个时间步进行预测更快。有关如何通过在相邻的单个时间步预测之间更新网络来预测将来时间步的示例，请参阅使用深度学习进行时间序列预测。

在绘图中可视化一些预测值。

idx = randperm(numel(YTest),4);
figure
for i = 1:numel(idx)
    subplot(2,2,i)
    
    plot(TTest{idx(i)},"--")
    hold on
    plot(YTest{idx(i)},".-")
    hold off
    
    ylim([0 thr + 25])
    title("Test Observation " + idx(i))
    xlabel("Time Step")
    ylabel("RUL")
end
legend(["Test Data" "Predicted"],Location="southeast")

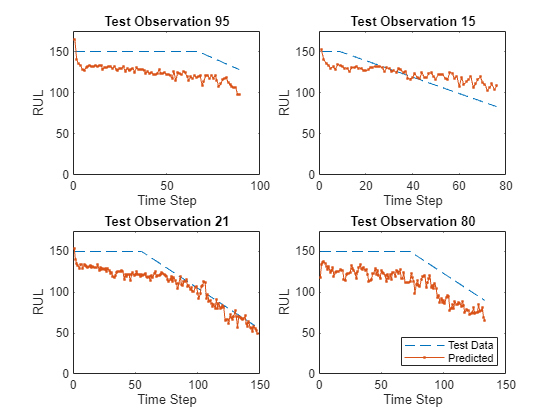
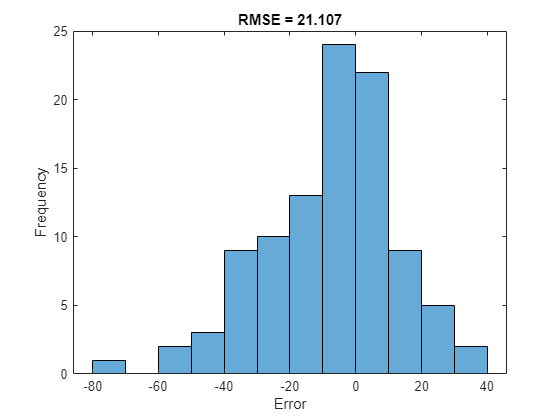
对于给定的不完整序列，预测的当前 RUL 是预测序列的最后一个元素。计算预测值的均方根误差 (RMSE)，并在直方图中可视化预测误差。

for i = 1:numel(TTest)
    TTestLast(i) = TTest{i}(end);
    YTestLast(i) = YTest{i}(end);
end
figure
rmse = sqrt(mean((YTestLast - TTestLast).^2))

rmse = single
    21.1070

histogram(YTestLast - TTestLast)
title("RMSE = " + rmse)
ylabel("Frequency")
xlabel("Error")

参考资料

Saxena, Abhinav, Kai Goebel, Don Simon, and Neil Eklund."Damage propagation modeling for aircraft engine run-to-failure simulation."In Prognostics and Health Management, 2008.PHM 2008.International Conference on, pp. 1-9.IEEE, 2008.

另请参阅