使用深度学习进行时间序列预测
此示例说明如何使用长期短期记忆 (LSTM) 网络预测时间序列数据。
LSTM 网络是一种循环神经网络 (RNN),它通过遍历时间步并更新 RNN 状态来处理输入数据。RNN 状态包含在所有先前时间步中记住的信息。您可以使用 LSTM 神经网络,通过将先前的时间步作为输入来预测时间序列或序列的后续值。要为时间序列预测训练 LSTM 神经网络,请训练具有序列输出的回归 LSTM 神经网络,其中响应(目标)是将值移位了一个时间步的训练序列。也就是说,在输入序列的每个时间步,LSTM 神经网络都学习预测下一个时间步的值。
有两种预测方法:开环预测和闭环预测。
开环预测 - 仅使用输入数据预测序列中的下一个时间步。对后续时间步进行预测时,需要从数据源中收集真实值并将其用作输入。例如,假设您要使用时间步 1 到 中收集的数据来预测序列的时间步 的值。要对时间步 进行预测,请等到记录下时间步 的真实值,并将其用作输入进行下一次预测。在进行下一次预测之前,如果有可以提供给 RNN 的真实值,则请使用开环预测。
闭环预测 - 通过使用先前的预测值作为输入来预测序列中的后续时间步。在这种情况下,模型不需要真实值便可进行预测。例如,假设您要仅使用在时间步 1 至 中收集的数据来预测序列的时间步 至 的值。要对时间步 进行预测,请使用时间步 的预测值作为输入。使用闭环预测来预测多个后续时间步,或在进行下一次预测之前没有真实值可提供给 RNN 时使用闭环预测。
此图显示使用闭环预测的预测值的序列示例。
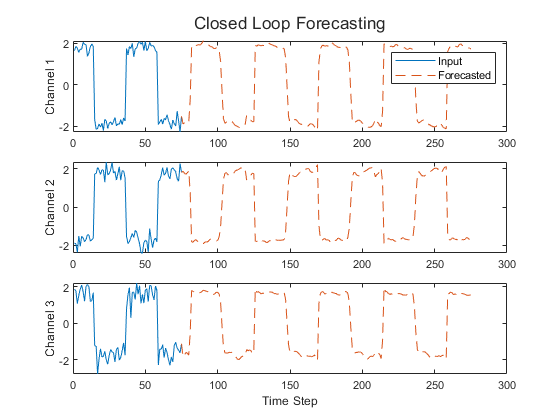
此示例使用 Waveform 数据集,它包含生成的 1000 个不同长度的合成波形,有三个通道。该示例训练一个 LSTM 神经网络,以同时使用闭环和开环预测根据先前时间步提供的值来预测波形的将来值。
加载数据
从 WaveformData.mat 加载示例数据。数据是序列的 numObservations×1 元胞数组,其中 numObservations 是序列数。每个序列都是一个 numTimeSteps×-numChannels 数值数组,其中 numTimeSteps 是序列的时间步,numChannels 是序列的通道数。
load WaveformData查看前几个序列的大小。
data(1:4)
ans=4×1 cell array
{103×3 double}
{136×3 double}
{140×3 double}
{124×3 double}
查看通道数。为了训练 LSTM 神经网络,每个序列必须具有相同数量的通道。
numChannels = size(data{1},2)numChannels = 3
可视化绘图中的前几个序列。
figure tiledlayout(2,2) for i = 1:4 nexttile stackedplot(data{i}) xlabel("Time Step") end
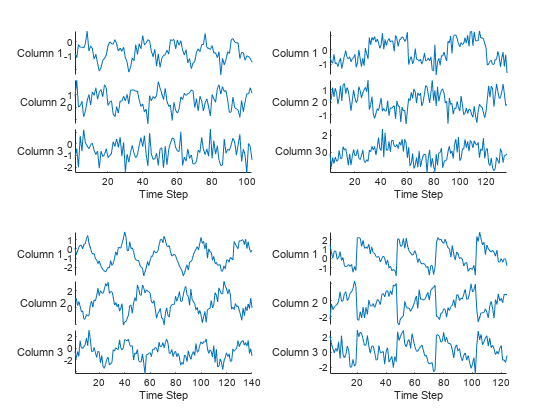
将数据划分为训练集和测试集。将 90% 的观测值用于训练,其余的用于测试。
numObservations = numel(data); idxTrain = 1:floor(0.9*numObservations); idxTest = floor(0.9*numObservations)+1:numObservations; dataTrain = data(idxTrain); dataTest = data(idxTest);
准备要训练的数据
要预测序列在将来时间步的值,请将目标指定为将值移位了一个时间步的训练序列。不要在训练序列中包含最终时间步。也就是说,在输入序列的每个时间步,LSTM 神经网络都学习预测下一个时间步的值。预测变量是没有最终时间步的训练序列。
numObservationsTrain = numel(dataTrain); XTrain = cell(numObservationsTrain,1); TTrain = cell(numObservationsTrain,1); for n = 1:numObservationsTrain X = dataTrain{n}; XTrain{n} = X(1:end-1,:); TTrain{n} = X(2:end,:); end
为了更好地拟合并防止训练发散,请将预测变量和目标值归一化,以使通道的均值和单位方差为零。在进行预测时,还必须使用与训练数据相同的统计量对测试数据进行归一化。
计算序列的每通道均值和标准差值。要轻松计算训练数据的均值和标准差,请使用 cell2mat 函数创建包含串联序列的数值数组。
muX = mean(cell2mat(XTrain)); sigmaX = std(cell2mat(XTrain),0); muT = mean(cell2mat(TTrain)); sigmaT = std(cell2mat(TTrain),0);
使用计算出的均值和标准差值对序列进行归一化。
for n = 1:numel(XTrain) XTrain{n} = (XTrain{n} - muX) ./ sigmaX; TTrain{n} = (TTrain{n} - muT) ./ sigmaT; end
定义 LSTM 神经网络架构
创建一个 LSTM 回归神经网络。
使用输入大小与输入数据的通道数匹配的序列输入层。
接下来,使用一个具有 128 个隐藏单元的 LSTM 层。隐藏单元的数量确定该层学习了多少信息。使用更多隐藏单元可以产生更准确的结果,但也更有可能导致训练数据过拟合。
要输出通道数与输入数据相同的序列,请包含一个输出大小与输入数据通道数匹配的全连接层。
layers = [
sequenceInputLayer(numChannels)
lstmLayer(128)
fullyConnectedLayer(numChannels)];指定训练选项
指定训练选项。
使用 Adam 优化进行训练。
进行 200 轮训练。对于较大的数据集,您可能不需要像良好拟合那样进行这么多轮训练。
在每个小批量中,对序列进行左填充,使它们具有相同的长度。左填充可以防止 RNN 预测序列末尾的填充值。
每轮训练都会打乱数据。
在绘图中显示训练进度。
禁用详尽输出。
options = trainingOptions("adam", ... MaxEpochs=200, ... SequencePaddingDirection="left", ... Shuffle="every-epoch", ... Plots="training-progress", ... Verbose=false);
训练循环神经网络
使用 trainnet 函数训练 LSTM 神经网络。对于回归,请使用均方误差损失。默认情况下,trainnet 函数使用 GPU(如果有)。使用 GPU 需要 Parallel Computing Toolbox™ 许可证和受支持的 GPU 设备。有关受支持设备的信息,请参阅GPU 计算要求 (Parallel Computing Toolbox)。否则,该函数使用 CPU。要指定执行环境,请使用 ExecutionEnvironment 训练选项。
net = trainnet(XTrain,TTrain,layers,"mse",options);
测试循环神经网络
使用与训练数据相同的步骤准备用于预测的测试数据。
使用从训练数据计算出的统计量来归一化测试数据。将目标指定为值移位了一个时间步的测试序列,将预测变量值指定为没有最终时间步的测试序列。
numObservationsTest = numel(dataTest); XTest = cell(numObservationsTest,1); TTest = cell(numObservationsTest,1); for n = 1:numObservationsTest X = dataTest{n}; XTest{n} = (X(1:end-1,:) - muX) ./ sigmaX; TTest{n} = (X(2:end,:) - muT) ./ sigmaT; end
使用 minibatchpredict 函数进行预测。默认情况下,minibatchpredict 函数使用 GPU(如果有)。使用与训练相同的填充选项填充序列。对于具有不同长度序列的“序列到序列”任务,通过将 UniformOutput 选项设置为 false,以元胞数组形式返回预测。
YTest = minibatchpredict(net,XTest, ... SequencePaddingDirection="left", ... UniformOutput=false);
对于每个测试序列,请计算预测值和目标值之间的均方根误差 (RMSE)。使用目标序列的长度作为参考,忽略预测序列中的任何填充值。
for n = 1:numObservationsTest T = TTest{n}; sequenceLength = size(T,1); Y = YTest{n}(end-sequenceLength+1:end,:); err(n) = rmse(Y,T,"all"); end
在直方图中可视化误差。值越低,表示准确度越高。
figure histogram(err) xlabel("RMSE") ylabel("Frequency")

计算所有测试观测值的 RMSE 均值。
mean(err,"all")ans = single
0.5096
预测将来时间步
给定输入时间序列或序列,要预测多个将来时间步的值,请使用 predict 函数一次预测一个时间步,并在每次预测时更新 RNN 状态。对于每次预测,使用前一次预测作为函数的输入。
在绘图中可视化其中一个测试序列。
idx = 2;
X = XTest{idx};
T = TTest{idx};
figure
stackedplot(X,DisplayLabels="Channel " + (1:numChannels))
xlabel("Time Step")
title("Test Observation " + idx)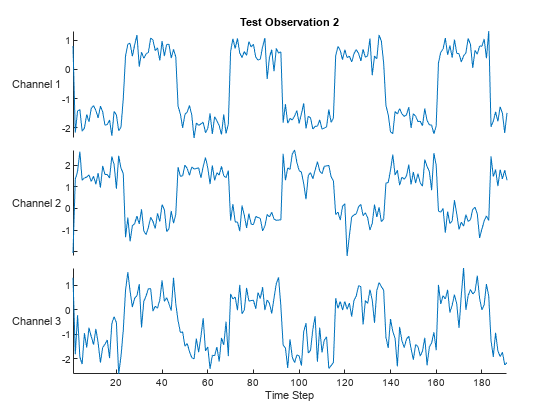
开环预测
开环预测仅使用输入数据预测序列中的下一个时间步。对后续时间步进行预测时,需要从数据源中收集真实值并将其用作输入。例如,假设您要使用时间步 1 到 中收集的数据来预测序列的时间步 的值。要对时间步 进行预测,请等到记录下时间步 的真实值,并将其用作输入进行下一次预测。在进行下一次预测之前,如果有可以提供给 RNN 的真实值,则请使用开环预测。
首先使用 resetState 函数重置状态来初始化 RNN 状态,然后使用输入数据的前几个时间步进行初始预测。使用输入数据的前 75 个时间步更新 RNN 状态。
net = resetState(net); offset = 75; [Z,state] = predict(net,X(1:offset,:)); net.State = state;
要进行进一步的预测,请遍历时间步并使用 predict 函数进行预测。每次预测后,更新 RNN 状态。通过遍历输入数据的时间步并将其用作 RNN 的输入,预测测试观测值的其余时间步的值。初始预测的最后一个时间步是第一个预测的时间步。
numTimeSteps = size(X,1); numPredictionTimeSteps = numTimeSteps - offset; Y = zeros(numPredictionTimeSteps,numChannels); Y(1,:) = Z(end,:); for t = 1:numPredictionTimeSteps-1 Xt = X(offset+t,:); [Y(t+1,:),state] = predict(net,Xt); net.State = state; end
将预测值与输入值进行比较。
figure t = tiledlayout(numChannels,1); title(t,"Open Loop Forecasting") for i = 1:numChannels nexttile plot(X(:,i)) hold on plot(offset:numTimeSteps,[X(offset,i) Y(:,i)'],"--") ylabel("Channel " + i) end xlabel("Time Step") nexttile(1) legend(["Input" "Forecasted"])
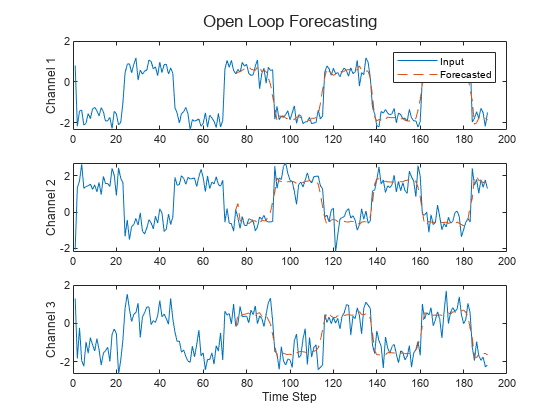
闭环预测
闭环预测通过使用先前的预测作为输入来预测序列中的后续时间步。在这种情况下,模型不需要真实值便可进行预测。例如,假设您要仅使用在时间步 1 至 中收集的数据来预测序列的时间步 至 的值。要对时间步 进行预测,请使用时间步 的预测值作为输入。使用闭环预测来预测多个后续时间步,或在进行下一次预测之前没有真实值可提供给 RNN 时使用闭环预测。
首先使用 resetState 函数重置状态来初始化 RNN 状态,然后使用输入数据的前几个时间步进行初始预测 Z。使用输入数据的所有时间步更新 RNN 状态。
net = resetState(net); offset = size(X,1); [Z,state] = predict(net,X(1:offset,:)); net.State = state;
要进行进一步的预测,请遍历时间步并使用 predict 函数进行预测。每次预测后,更新 RNN 状态。通过将先前的预测值迭代传递给 RNN 来预测接下来的 200 个时间步。由于 RNN 不需要输入数据来进行任何进一步的预测,因此您可以指定任意数量的时间步来进行预测。初始预测的最后一个时间步是第一个预测的时间步。
numPredictionTimeSteps = 200; Y = zeros(numPredictionTimeSteps,numChannels); Y(1,:) = Z(end,:); for t = 2:numPredictionTimeSteps [Y(t,:),state] = predict(net,Y(t-1,:)); net.State = state; end
在绘图中可视化预测值。
numTimeSteps = offset + numPredictionTimeSteps; figure t = tiledlayout(numChannels,1); title(t,"Closed Loop Forecasting") for i = 1:numChannels nexttile plot(X(1:offset,i)) hold on plot(offset:numTimeSteps,[X(offset,i) Y(:,i)'],"--") ylabel("Channel " + i) end xlabel("Time Step") nexttile(1) legend(["Input" "Forecasted"])
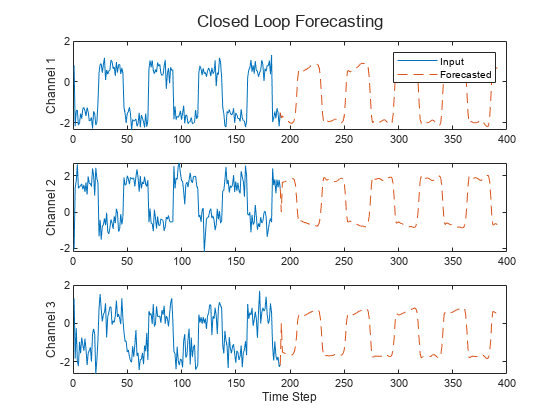
闭环预测允许您预测任意数量的时间步,但与开环预测相比,其准确度可能会降低,因为 RNN 在预测过程中不会访问真实值。
另请参阅
trainnet | trainingOptions | dlnetwork | lstmLayer | sequenceInputLayer