训练变分自编码器 (VAE) 以生成图像

此示例说明如何训练深度学习变分自编码器 (VAE) 来生成图像。

要生成充分代表数据集合中观测值的数据，可以使用变分自编码器。自编码器是一种模型，它被训练为通过将输入变换为低维空间（编码步骤）并从低维表示中重新构造输入（解码步骤）来复制其输入。

下图说明重新构造数字图像的自编码器的基本结构。

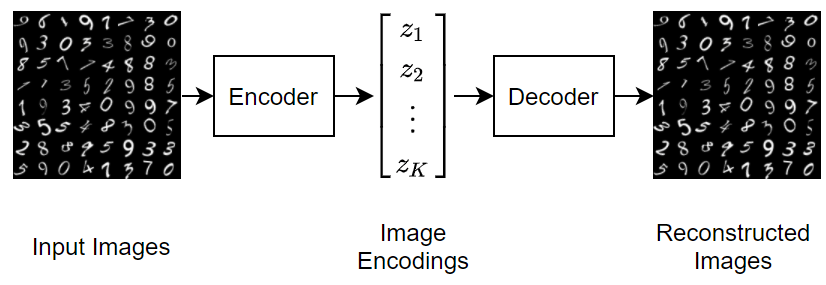
要使用变分自编码器生成新图像，请向解码器输入随机向量。

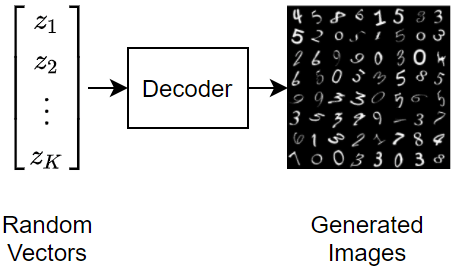
变分自编码器与常规自编码器的不同之处在于，前者在潜在空间上施加概率分布，并学习该分布，使得来自解码器的输出的分布与观测到的数据的分布相匹配。特别是，潜在输出是从编码器学习到的分布中随机采样得来的。

加载数据

使用 digitTrain4DArrayData 和 digitTest4DArrayData 函数将数字数据加载为内存数值数组。Digits 数据集由 10000 个内容是手写数字的合成灰度图像组成。每个图像为 28×28 像素。

XTrain = digitTrain4DArrayData;
XTest = digitTest4DArrayData;

定义网络架构

自编码器有两个部分：编码器和解码器。编码器接受图像输入，并使用一系列下采样操作（如卷积）输出潜在向量表示（编码）。同样，解码器接受潜在向量表示作为输入，并使用一系列上采样操作（如转置卷积）来重新构造输入。

为了对输入进行采样，该示例使用自定义层 samplingLayer。要访问此层，请以实时脚本形式打开此示例。该层接受使用对数方差向量 $log (σ^{2})$ 串联的均值向量 $μ$ 作为输入，并对 $N (μ_{i}, σ_{i}^{2})$ 的元素进行采样。该层使用对数方差使训练过程在数值上更加稳定。

定义编码器网络架构

定义以下编码器网络，将 28×28×1 图像下采样为 32×1 潜在向量。

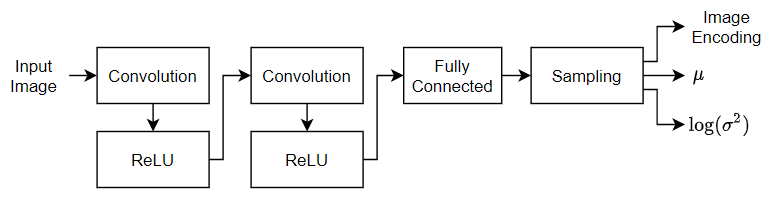
对于图像输入，请指定输入大小与训练数据匹配的图像输入层。不要对数据进行归一化。
要对输入进行下采样，请指定两个由二维卷积层和 ReLU 层组成的模块。
要输出均值和对数方差的串联向量，请指定一个输出通道数是潜在通道数的两倍的全连接层。
要对统计量指定的编码进行采样，请使用自定义层 samplingLayer 来包含一个采样层。要访问此层，请以实时脚本形式打开此示例。

numLatentChannels = 32;
imageSize = [28 28 1];

layersE = [
    imageInputLayer(imageSize,Normalization="none")
    convolution2dLayer(3,32,Padding="same",Stride=2)
    reluLayer
    convolution2dLayer(3,64,Padding="same",Stride=2)
    reluLayer
    fullyConnectedLayer(2*numLatentChannels)
    samplingLayer];

定义解码器网络架构

定义以下解码器网络，该网络基于 32×1 潜在向量重新构造 28×28×1 图像。

对于特征向量输入，指定一个输入大小与潜在通道数匹配的特征输入层。
使用自定义层 projectAndReshapeLayer（该自定义层以支持文件的形式包含在此示例中）将潜在输入投影并重构为 7×7×64 数组。要访问此层，请以实时脚本形式打开此示例。将投影大小指定为 [7 7 64]。
要对输入进行上采样，请指定两个由转置卷积层和 ReLU 层组成的模块。
要输出大小为 28×28×1 的图像，请包含一个具有 3×3 滤波器的转置卷积层。
要将输出映射到 [0,1] 范围内的值，请包括 sigmoid 激活层。

projectionSize = [7 7 64];
numInputChannels = imageSize(3);

layersD = [
    featureInputLayer(numLatentChannels)
    projectAndReshapeLayer(projectionSize)
    transposedConv2dLayer(3,64,Cropping="same",Stride=2)
    reluLayer
    transposedConv2dLayer(3,32,Cropping="same",Stride=2)
    reluLayer
    transposedConv2dLayer(3,numInputChannels,Cropping="same")
    sigmoidLayer];

要使用自定义训练循环训练两个网络并支持自动微分，请将层数组转换为 dlnetwork 对象。

netE = dlnetwork(layersE);
netD = dlnetwork(layersD);

定义模型损失函数

定义一个函数，该函数返回模型损失和损失关于可学习参数的梯度。

modelLoss 函数（在示例的模型损失函数部分中定义）接受编码器和解码器网络以及小批量输入数据作为输入，并返回损失以及损失关于网络中可学习参数的梯度。为了计算损失，该函数使用 ELBOloss 函数（在示例的 ELBO 损失函数部分中定义），接受编码器输出的均值和对数方差作为输入，并使用它们来计算证据下界 (ELBO) 损失。

指定训练选项

使用 128 的小批量大小和 0.001 的学习率进行 150 轮训练。

numEpochs = 150;
miniBatchSize = 128;
learnRate = 1e-3;

训练模型

使用自定义训练循环训练模型。

创建一个 minibatchqueue 对象，用于在训练期间处理和管理小批量图像。对于每个小批量：

将训练数据转换为数组数据存储。指定对第四个维度进行迭代。
使用自定义小批量预处理函数 preprocessMiniBatch（在此示例末尾定义）将多个观测值串联成单个小批量。
用维度标签 "SSCB"（空间、空间、通道、批量）格式化图像数据。默认情况下，minibatchqueue 对象将数据转换为基础类型为 single 的 dlarray 对象。
在 GPU 上（如果有）进行训练。默认情况下，如果 GPU 可用，则 minibatchqueue 对象会将每个输出都转换为一个 gpuArray。使用 GPU 需要 Parallel Computing Toolbox™ 和支持的 GPU 设备。有关受支持设备的信息，请参阅GPU Computing Requirements (Parallel Computing Toolbox)。
为确保所有小批量都具有相同的大小，请丢弃任何不完整小批量。

dsTrain = arrayDatastore(XTrain,IterationDimension=4);
numOutputs = 1;

mbq = minibatchqueue(dsTrain,numOutputs, ...
    MiniBatchSize = miniBatchSize, ...
    MiniBatchFcn=@preprocessMiniBatch, ...
    MiniBatchFormat="SSCB", ...
    PartialMiniBatch="discard");

初始化 Adam 求解器的参数。

trailingAvgE = [];
trailingAvgSqE = [];
trailingAvgD = [];
trailingAvgSqD = [];

计算训练进度监视器的总迭代次数

numObservationsTrain = size(XTrain,4);
numIterationsPerEpoch = ceil(numObservationsTrain / miniBatchSize);
numIterations = numEpochs * numIterationsPerEpoch;

初始化训练进度监视器。由于计时器在您创建监视器对象时启动，请确保您创建的对象靠近训练循环。

monitor = trainingProgressMonitor( ...
    Metrics="Loss", ...
    Info="Epoch", ...
    XLabel="Iteration");

使用自定义训练循环来训练网络。对于每轮训练，对数据进行乱序处理，并遍历小批量数据。对于每个小批量：

使用 dlfeval 和 modelLoss 函数计算模型损失和梯度。
使用 adamupdate 函数更新编码器和解码器网络参数。
显示训练进度。

epoch = 0;
iteration = 0;

% Loop over epochs.
while epoch < numEpochs && ~monitor.Stop
    epoch = epoch + 1;

    % Shuffle data.
    shuffle(mbq);

    % Loop over mini-batches.
    while hasdata(mbq) && ~monitor.Stop
        iteration = iteration + 1;

        % Read mini-batch of data.
        X = next(mbq);

        % Evaluate loss and gradients.
        [loss,gradientsE,gradientsD] = dlfeval(@modelLoss,netE,netD,X);

        % Update learnable parameters.
        [netE,trailingAvgE,trailingAvgSqE] = adamupdate(netE, ...
            gradientsE,trailingAvgE,trailingAvgSqE,iteration,learnRate);

        [netD, trailingAvgD, trailingAvgSqD] = adamupdate(netD, ...
            gradientsD,trailingAvgD,trailingAvgSqD,iteration,learnRate);

        % Update the training progress monitor. 
        recordMetrics(monitor,iteration,Loss=loss);
        updateInfo(monitor,Epoch=epoch + " of " + numEpochs);
        monitor.Progress = 100*iteration/numIterations;
    end
end

测试网络

用保留的测试集测试经过训练的自编码器。使用与训练数据相同的步骤创建数据的小批量队列，但不要丢弃任何不完整小批量数据。

dsTest = arrayDatastore(XTest,IterationDimension=4);
numOutputs = 1;

mbqTest = minibatchqueue(dsTest,numOutputs, ...
    MiniBatchSize = miniBatchSize, ...
    MiniBatchFcn=@preprocessMiniBatch, ...
    MiniBatchFormat="SSCB");

使用 modelPredictions 函数和经过训练的自编码器进行预测。

YTest = modelPredictions(netE,netD,mbqTest);

通过接受测试图像和重新构图像的均方误差并在直方图中对它们进行可视化，以此可视化重新构造误差。

err = mean((XTest-YTest).^2,[1 2 3]);
figure
histogram(err)
xlabel("Error")
ylabel("Frequency")
title("Test Data")

生成新图像

通过解码器传递随机采样的图像编码，生成一批新图像。

numImages = 64;

ZNew = randn(numLatentChannels,numImages);
ZNew = dlarray(ZNew,"CB");

YNew = predict(netD,ZNew);
YNew = extractdata(YNew);

在图窗中显示生成的图像。

figure
I = imtile(YNew);
imshow(I)
title("Generated Images")

现在，VAE 已学会强特征表示，这使它能够生成类似于训练数据的图像。

辅助函数

模型损失函数

modelLoss 函数接受编码器和解码器网络以及输入数据的一个小批量作为输入，并返回损失以及损失关于网络中可学习参数的梯度。该函数通过编码器传递训练图像，并通过解码器传递生成的图像编码。为了计算损失，该函数使用 elboLoss 函数以及编码器采样层输出的均值和对数方差统计量。

function [loss,gradientsE,gradientsD] = modelLoss(netE,netD,X)

% Forward through encoder.
[Z,mu,logSigmaSq] = forward(netE,X);

% Forward through decoder.
Y = forward(netD,Z);

% Calculate loss and gradients.
loss = elboLoss(Y,X,mu,logSigmaSq);
[gradientsE,gradientsD] = dlgradient(loss,netE.Learnables,netD.Learnables);

end

ELBO 损失函数

ELBOloss 函数接受编码器输出的均值和对数方差，并使用它们来计算证据下界 (ELBO) 损失。ELBO 损失由两个单独的损失项相加得出：

$ELBO loss = reconstruction loss + KL loss$ .

重建损失通过使用均方误差 (MSE) 来测量解码器输出与原始输入的接近程度：

$reconstruction loss = MSE (reconstructed image, input image)$ .

KL 损失，即 Kullback–Leibler 散度，测量两个概率分布之间的差异。在本例中，最小化 KL 损失意味着确保学习的均值和方差尽可能接近目标（正态）分布的均值和方差。对于大小为 $K$ 的潜在维度，KL 损失的计算公式如下

$KL loss = - 0.5 \cdot \sum_{i = 1}^{K} (1 + \log (σ_{i}^{2}) - μ_{i}^{2} - σ_{i}^{2})$ .

包含 KL 损失项的实际效果是将由于重建损失而学习到的聚类紧密地聚集在潜在空间中心周围，形成连续的采样空间。

function loss = elboLoss(Y,T,mu,logSigmaSq)

% Reconstruction loss.
reconstructionLoss = mse(Y,T);

% KL divergence.
KL = -0.5 * sum(1 + logSigmaSq - mu.^2 - exp(logSigmaSq),1);
KL = mean(KL);

% Combined loss.
loss = reconstructionLoss + KL;

end

模型预测函数

modelPredictions 函数接受编码器和解码器网络对象以及输入数据 mbq 的 minibatchqueue 作为输入，并通过迭代 minibatchqueue 对象中的所有数据来计算模型预测。

function Y = modelPredictions(netE,netD,mbq)

Y = [];

% Loop over mini-batches.
while hasdata(mbq)
    X = next(mbq);

    % Forward through encoder.
    Z = predict(netE,X);

    % Forward through dencoder.
    XGenerated = predict(netD,Z);

    % Extract and concatenate predictions.
    Y = cat(4,Y,extractdata(XGenerated));
end

end

小批量预处理函数

preprocessMiniBatch 函数通过串联第四个维度上的输入来预处理小批量预测变量。

function X = preprocessMiniBatch(dataX)

% Concatenate.
X = cat(4,dataX{:});

end

另请参阅