Frequency-Domain Adaptive Filter
Compute output, error, and coefficients using frequency domain FIR adaptive filter
Libraries:
DSP System Toolbox /
Filtering /
Adaptive Filters
Description
The Frequency-Domain Adaptive Filter block implements an adaptive finite impulse response (FIR) filter in the frequency domain using the fast block least mean squares (LMS) algorithm. The Filter length and the Block length parameters specify the filter length and the block length values the algorithm uses. When you select the Output filter FFT coefficients check box, the block outputs the discrete Fourier transform of the current filter coefficients. The block offers the constrained and unconstrained versions of the algorithm with partitioned and nonpartitioned modes. For details, see Algorithms.
Ports
Input
The signal to be filtered by the frequency-domain FIR adaptive filter. The data input and the desired signal input must have the same size and data type. The length of the input vector must be divisible by the Block length parameter value.
The data input can be a variable-size signal as long as the frame length is a multiple of the Block length. You can change the number of elements in the column vector during the model simulation.
Data Types: single | double
Complex Number Support: Yes
The frequency-domain adaptive filter adapts its filter weights to minimize the error, Error, and converge the input signal to match the desired signal as closely as possible.
The data input and the desired signal must have the same size and data type. The length of the desired signal vector must be divisible by the Block length parameter value.
The desired signal can be a variable-size signal as long as the frame length is a multiple of the Block length. You can change the number of elements in the column vector during the model simulation.
Data Types: single | double
Complex Number Support: Yes
Adaptation step size factor, specified as a real scalar in the range
(0,1]. Using a small step size ensures a small steady-state error.
However, a small step size decreases the resulting convergence speed of
the adaptive filter. Increasing the step size improves the convergence
speed, at the cost of increased steady-state mean squared error. When
the step size value is 1, the algorithm provides the
optimal tradeoff between the convergence speed and the steady-state mean
squared error.
Dependencies
This port appears when you select the Specify step size from port parameter.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
Leakage factor used in leaky adaptive filter, specified as a real
scalar in the range (0,1]. When the value is less than 1, the block
implements a leaky adaptive algorithm. When the value is
1, the block provides no leakage in the adapting
method.
Dependencies
This port appears when you select the Specify leakage factor from port check box.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
Averaging factor used to compute the exponentially windowed fast Fourier transform (FFT) input signal powers for the coefficient updates, specified as a real scalar in the range (0,1].
Dependencies
This port appears when you select the Specify averaging factor from port check box.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
Offset for the normalization terms in the coefficient updates, specified as a nonnegative real scalar value. Use this value to avoid division by zero or division by very small numbers if any of the FFT input signal powers become very small.
Dependencies
This port appears when you select the Specify offset from port check box.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
If you input a nonzero scalar value through this port, the block continuously updates its filter coefficients. If you input a zero through this port, the filter coefficients do not update, and their values remain at the current value.
Dependencies
This port appears when you select the Enable adapt port check box.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
If you input a nonzero scalar value through this port, the block resets all internal states. If you input a zero through this port, the internal states are not reset.
Dependencies
This port appears when you select the Enable reset port check box.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
Output
Filtered output, returned as a column vector. The block adapts its filter weights to converge the input signal to match the desired signal as closely as possible. The filter outputs the converged signal.
Data Types: single | double
Complex Number Support: Yes
Difference between the output signal and the desired signal, returned as a column vector. The objective of the adaptive filter is to minimize this error. The block adapts its weights to converge towards optimal filter weights which produce an output signal that matches the desired signal as closely as possible. For more details on how Error is computed, see References.
Data Types: single | double
Complex Number Support: Yes
Current discrete Fourier transform of the filter coefficients,
returned as a row vector. For Constrained
FDAF and Unconstrained FDAF
algorithms, the length of this vector is equal to the sum of the
Filter length value and the Block
length value. This port initially outputs the FFT values
of the Initial time-domain coefficients parameter.
During the model simulation, this port outputs the FFT values of the
current filter coefficients.
Dependencies
This port appears when you select the Output filter FFT coefficients check box.
Data Types: single | double
Complex Number Support: Yes
Parameters
Method used to calculate the filter coefficients, specified as::
Constrained FDAF–– Imposes a gradient constraint on the filter tap weights.Partitioned constrained FDAF–– Partitions the impulse response of the filter to reduce latency.Unconstrained FDAF–– No gradient constraint is imposed on the filter tap weights.Partitioned unconstrained FDAF–– Partitions the impulse response of the filter to reduce latency. No gradient constraint is imposed on the filter tap weights.
For more details, see Algorithms.
Length of the FIR filter coefficients vector, specified as a positive, integer-valued scalar.
Block length for the coefficients update, specified as a positive, integer-valued scalar. The adaptive filter processes the input data and the desired signal as a block of samples of length set by this parameter. For details on how this data is processed by the filter, see Algorithms. The length of the input vector must be divisible by the Block length parameter value. The default value of the Block length parameter is set to the value of the Filter length parameter.
When you select this check box, the adaptation step size is input through the Mu port. When you clear this check box, the step size is specified on the block dialog through the Step size parameter.
Adaptation step size factor, specified as a real scalar in the range
(0,1]. Setting the Step size parameter to
1 provides the fastest convergence during
adaptation.
Tunable: Yes
Dependencies
This parameter appears when you clear the Specify step size from port check box.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
When you select this check box, the leakage factor is input through the Leak port. When you clear this check box, the leakage factor is specified on the block dialog through the Leakage factor parameter.
Leakage factor used in leaky adaptive filter, specified as a real scalar
in the range (0,1]. When the value is less than 1, the
block implements a leaky adaptive algorithm. When the value is
1, the block provides no leakage in the adapting
method.
Tunable: Yes
Dependencies
This parameter appears when you clear the Specify leakage factor from port check box.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
When you select this check box, the averaging factor for signal power is input through the Avrg port. When you clear this check box, the averaging factor is specified on the block dialog through the Averaging factor parameter.
Averaging factor used to compute the exponentially windowed FFT input signal powers for the coefficient updates, specified as a real scalar in the range (0,1].
Tunable: Yes
Dependencies
This parameter appears when you clear the Specify averaging factor from port check box.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
When you select this check box, the offset for the normalization terms in the coefficient updates is input through the Offset port. When you clear this check box, the offset is specified on the block dialog through the Offset parameter.
Offset for the normalization terms in the coefficient updates, specified as a nonnegative real scalar value. Use this value to avoid division by zero or division by very small numbers if any of the FFT input signal powers become very small.
Tunable: Yes
Dependencies
This parameter appears when you clear the Specify offset from port check box.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
Initial common value of all of the FFT input signal powers, specified as a positive numeric scalar value.
If you change this value during the simulation, the change takes effect only after a reset event occurs.
Tunable: Yes
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
Initial time-domain coefficients of the adaptive filter, specified as a scalar or a vector of length equal to the value you specify in the Filter length parameter. The adaptive filter block uses these coefficients to compute the initial frequency-domain filter coefficients.
If you change this value during the simulation, the change takes effect only after a reset event occurs.
Tunable: Yes
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32
When you select this check box, the Adapt input port is enabled. If you input a nonzero scalar value through this port, the block continuously updates its filter coefficients. If you input a zero through this port, the filter coefficients do not update and their values remain at the current value.
When you select this check box, the Reset input port is enabled. If you input a nonzero scalar value through this port, the block resets all internal states. If you input a zero through this port, the internal states are not reset.
When you select this check box, the FFTCoeffs output port is enabled. Through this port, the block outputs the discrete Fourier transform of the current filter coefficients.
Specify the type of simulation to run. You can set this parameter to:
Interpreted execution–– Simulate model using the MATLAB® interpreter. This option shortens startup time.Code generation–– Simulate model using generated C code. The first time you run a simulation, Simulink® generates C code for the block. The C code is reused for subsequent simulations as long as the model does not change. This option requires additional startup time but provides faster subsequent simulations.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
Algorithms
Frequency-domain adaptive filtering consists of three steps - filtering, error estimation, and
tap-weight adaptation. This algorithm implements FIR filtering in the frequency domain using
the overlap-save or overlap-add method. For more implementation details of these two
methods, see the Algorithms section in the dsp.FrequencyDomainFIRFilter
object page. The error estimation and the tap-weight adaptation are implemented using the
fast block LMS algorithm (FBLMS).
The frequency-domain adaptive filter processes input data and the desired signal data as a block of samples using the fast block LMS (FBLMS) algorithm. Here is the block diagram of the frequency-domain adaptive filter using the FBLMS algorithm. The frequency-domain FIR filter in this diagram uses the overlap-save method.
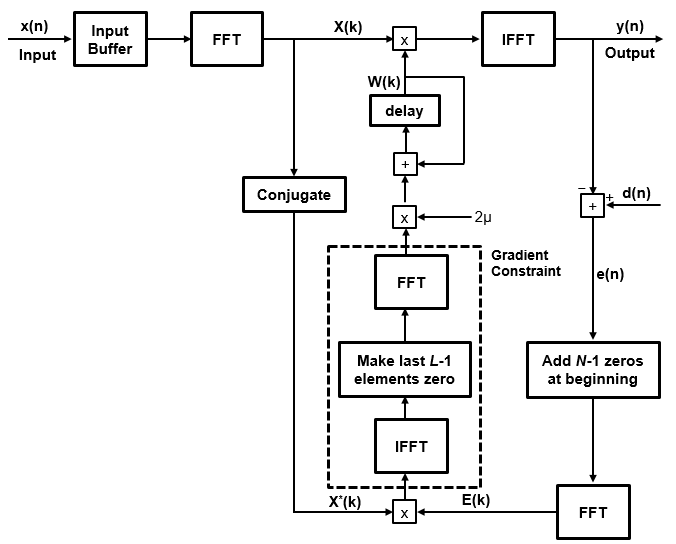
where:
N –– Filter length
L –– Block length
μ –– Step size parameter
x(n) –– Input signal
X(k) –– Transformed input signal in the frequency domain
d(n) –– Desired signal
e(n) –– Error between the desired signal and the filter output
E(n) –– Transformed error signal in the frequency domain
W(k) –– Tap-weights vector in the frequency domain
For more details on how the error is estimated and the tap-weights are adapted, see [2].
The previous diagram is the constrained version. If you remove the gradient constraint portion of the algorithm, you have the unconstrained FBLMS implementation. For details on the convergence behavior of both constrained and unconstrained variations, see [2].
The latency of the filter roughly equals the length of the FIR numerator. If the impulse response of the filter is very long, the latency becomes significantly large. The partitioned FBLMS algorithm reduces latency by partitioning the impulse response. The nonpartitioned frequency-domain FIR filtering is faster than the time-domain filtering for long impulse responses, at the cost of increased latency. To mitigate the latency and make the frequency domain filtering even more efficient, the algorithm partitions the impulse response into multiple short blocks and performs overlap-save or overlap-add on each block. The results of the different blocks are then combined to obtain the final output. The latency of this approach is of the order of the block length, rather than the entire impulse response length. This reduced latency comes at the cost of additional computation. For more details on the implementation, see [2].
References
[1] Shynk, J.J."Frequency-Domain and Multirate Adaptive Filtering." IEEE Signal Processing Magazine, Vol. 9, No. 1, pp. 14–37, Jan. 1992.
[2] Farhang-Boroujeny, B., Adaptive Filters: Theory and Applications, Chichester, England, Wiley, 1998.
[3] Stockham, T. G., Jr. "High Speed Convolution and Correlation." Proceedings of the 1966 Spring Joint Computer Conference, AFIPS, Vol 28, 1966, pp. 229–233.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2018aThe default value of the Simulate using parameter is now
Interpreted execution. With this change, the block uses the
MATLAB interpreter for simulation by default.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)