Main Content

fitmodel

Fit logistic regression model to Weight of Evidence (WOE) data

collapse all in page

Syntax

sc = fitmodel(sc)
[sc,mdl] = fitmodel(sc)
[sc,mdl] = fitmodel(___,Name,Value)

Description

sc = fitmodel(sc) fits a logistic regression model to the Weight of Evidence (WOE) data and stores the model predictor names and corresponding coefficients in the creditscorecard object.

fitmodel internally transforms all the predictor variables into WOE values, using the bins found with the automatic or manual binning process. The response variable is mapped so that "Good" is 1, and "Bad" is 0. This implies that higher (unscaled) scores correspond to better (less risky) individuals (smaller probability of default).

Alternatively, you can use setmodel to provide names of the predictors that you want in the logistic regression model, along with their corresponding coefficients.

example

[sc,mdl] = fitmodel(sc) fits a logistic regression model to the Weight of Evidence (WOE) data and stores the model predictor names and corresponding coefficients in the creditscorecard object. fitmodel returns an updated creditscorecard object and a GeneralizedLinearModel object containing the fitted model.

fitmodel internally transforms all the predictor variables into WOE values, using the bins found with the automatic or manual binning process. The response variable is mapped so that "Good" is 1, and "Bad" is 0. This implies that higher (unscaled) scores correspond to better (less risky) individuals (smaller probability of default).

Alternatively, you can use setmodel to provide names of the predictors that you want in the logistic regression model, along with their corresponding coefficients.

example

[sc,mdl] = fitmodel(___,Name,Value) fits a logistic regression model to the Weight of Evidence (WOE) data using optional name-value pair arguments and stores the model predictor names and corresponding coefficients in the creditscorecard object. Using name-value pair arguments, you can select which Generalized Linear Model to fit the data. fitmodel returns an updated creditscorecard object and a GeneralizedLinearModel object containing the fitted model.

example

Examples

collapse all

Open Live Script

Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011). 

load CreditCardData
sc = creditscorecard(data,'IDVar','CustID')
sc = 
  creditscorecard with properties:

                GoodLabel: 0
              ResponseVar: 'status'
               WeightsVar: ''
                 VarNames: {'CustID'  'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'  'status'}
        NumericPredictors: {'CustAge'  'TmAtAddress'  'CustIncome'  'TmWBank'  'AMBalance'  'UtilRate'}
    CategoricalPredictors: {'ResStatus'  'EmpStatus'  'OtherCC'}
           BinMissingData: 0
                    IDVar: 'CustID'
            PredictorVars: {'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'}
                     Data: [1200x11 table]

Perform automatic binning. 

sc = autobinning(sc)
sc = 
  creditscorecard with properties:

                GoodLabel: 0
              ResponseVar: 'status'
               WeightsVar: ''
                 VarNames: {'CustID'  'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'  'status'}
        NumericPredictors: {'CustAge'  'TmAtAddress'  'CustIncome'  'TmWBank'  'AMBalance'  'UtilRate'}
    CategoricalPredictors: {'ResStatus'  'EmpStatus'  'OtherCC'}
           BinMissingData: 0
                    IDVar: 'CustID'
            PredictorVars: {'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'}
                     Data: [1200x11 table]

Use fitmodel to fit a logistic regression model using Weight of Evidence (WOE) data. fitmodel internally transforms all the predictor variables into WOE values, using the bins found with the automatic binning process. fitmodel then fits a logistic regression model using a stepwise method (by default). 

sc = fitmodel(sc);
1. Adding CustIncome, Deviance = 1490.8527, Chi2Stat = 32.588614, PValue = 1.1387992e-08
2. Adding TmWBank, Deviance = 1467.1415, Chi2Stat = 23.711203, PValue = 1.1192909e-06
3. Adding AMBalance, Deviance = 1455.5715, Chi2Stat = 11.569967, PValue = 0.00067025601
4. Adding EmpStatus, Deviance = 1447.3451, Chi2Stat = 8.2264038, PValue = 0.0041285257
5. Adding CustAge, Deviance = 1441.994, Chi2Stat = 5.3511754, PValue = 0.020708306
6. Adding ResStatus, Deviance = 1437.8756, Chi2Stat = 4.118404, PValue = 0.042419078
7. Adding OtherCC, Deviance = 1433.707, Chi2Stat = 4.1686018, PValue = 0.041179769

Generalized linear regression model:
    logit(status) ~ 1 + CustAge + ResStatus + EmpStatus + CustIncome + TmWBank + OtherCC + AMBalance
    Distribution = Binomial

Estimated Coefficients:
                   Estimate       SE       tStat       pValue  
                   ________    ________    ______    __________

    (Intercept)    0.70239     0.064001    10.975    5.0538e-28
    CustAge        0.60833      0.24932      2.44      0.014687
    ResStatus        1.377      0.65272    2.1097      0.034888
    EmpStatus      0.88565        0.293    3.0227     0.0025055
    CustIncome     0.70164      0.21844    3.2121     0.0013179
    TmWBank         1.1074      0.23271    4.7589    1.9464e-06
    OtherCC         1.0883      0.52912    2.0569      0.039696
    AMBalance        1.045      0.32214    3.2439     0.0011792


1200 observations, 1192 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 89.7, p-value = 1.4e-16

This example uses:

Open Live Script

Use the CreditCardData.mat file to load the data (dataWeights) that contains a column (RowWeights) for the weights (using a dataset from Refaat 2011). 

load CreditCardData

Create a creditscorecard object using the optional name-value pair argument for 'WeightsVar'. 

sc = creditscorecard(dataWeights,'IDVar','CustID','WeightsVar','RowWeights')
sc = 
  creditscorecard with properties:

                GoodLabel: 0
              ResponseVar: 'status'
               WeightsVar: 'RowWeights'
                 VarNames: {'CustID'  'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'  'RowWeights'  'status'}
        NumericPredictors: {'CustAge'  'TmAtAddress'  'CustIncome'  'TmWBank'  'AMBalance'  'UtilRate'}
    CategoricalPredictors: {'ResStatus'  'EmpStatus'  'OtherCC'}
           BinMissingData: 0
                    IDVar: 'CustID'
            PredictorVars: {'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'}
                     Data: [1200x12 table]

Perform automatic binning.

sc = autobinning(sc)
sc = 
  creditscorecard with properties:

                GoodLabel: 0
              ResponseVar: 'status'
               WeightsVar: 'RowWeights'
                 VarNames: {'CustID'  'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'  'RowWeights'  'status'}
        NumericPredictors: {'CustAge'  'TmAtAddress'  'CustIncome'  'TmWBank'  'AMBalance'  'UtilRate'}
    CategoricalPredictors: {'ResStatus'  'EmpStatus'  'OtherCC'}
           BinMissingData: 0
                    IDVar: 'CustID'
            PredictorVars: {'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'}
                     Data: [1200x12 table]

Use fitmodel to fit a logistic regression model using Weight of Evidence (WOE) data. fitmodel internally transforms all the predictor variables into WOE values, using the bins found with the automatic binning process. fitmodel then fits a logistic regression model using a stepwise method (by default). When the optional name-value pair argument 'WeightsVar' is used to specify observation (sample) weights, the mdl output uses the weighted counts with stepwiseglm and fitglm.

[sc,mdl] = fitmodel(sc);
1. Adding CustIncome, Deviance = 764.3187, Chi2Stat = 15.81927, PValue = 6.968927e-05
2. Adding TmWBank, Deviance = 751.0215, Chi2Stat = 13.29726, PValue = 0.0002657942
3. Adding AMBalance, Deviance = 743.7581, Chi2Stat = 7.263384, PValue = 0.007037455

Generalized linear regression model:
    logit(status) ~ 1 + CustIncome + TmWBank + AMBalance
    Distribution = Binomial

Estimated Coefficients:
                   Estimate       SE       tStat       pValue  
                   ________    ________    ______    __________

    (Intercept)    0.70642     0.088702     7.964    1.6653e-15
    CustIncome      1.0268      0.25758    3.9862    6.7132e-05
    TmWBank         1.0973      0.31294    3.5063     0.0004543
    AMBalance       1.0039      0.37576    2.6717     0.0075464


1200 observations, 1196 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 36.4, p-value = 6.22e-08
Open Live Script

Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011). 

load CreditCardData
sc = creditscorecard(data,'IDVar','CustID')
sc = 
  creditscorecard with properties:

                GoodLabel: 0
              ResponseVar: 'status'
               WeightsVar: ''
                 VarNames: {'CustID'  'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'  'status'}
        NumericPredictors: {'CustAge'  'TmAtAddress'  'CustIncome'  'TmWBank'  'AMBalance'  'UtilRate'}
    CategoricalPredictors: {'ResStatus'  'EmpStatus'  'OtherCC'}
           BinMissingData: 0
                    IDVar: 'CustID'
            PredictorVars: {'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'}
                     Data: [1200x11 table]

Perform automatic binning. 

sc = autobinning(sc,'Algorithm','EqualFrequency')
sc = 
  creditscorecard with properties:

                GoodLabel: 0
              ResponseVar: 'status'
               WeightsVar: ''
                 VarNames: {'CustID'  'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'  'status'}
        NumericPredictors: {'CustAge'  'TmAtAddress'  'CustIncome'  'TmWBank'  'AMBalance'  'UtilRate'}
    CategoricalPredictors: {'ResStatus'  'EmpStatus'  'OtherCC'}
           BinMissingData: 0
                    IDVar: 'CustID'
            PredictorVars: {'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'}
                     Data: [1200x11 table]

Use fitmodel to fit a logistic regression model using Weight of Evidence (WOE) data. fitmodel internally transforms all the predictor variables into WOE values, using the bins found with the automatic binning process. Set the VariableSelection name-value pair argument to FullModel to specify that all predictors must be included in the fitted logistic regression model. 

sc = fitmodel(sc,'VariableSelection','FullModel');
Generalized linear regression model:
    logit(status) ~ 1 + CustAge + TmAtAddress + ResStatus + EmpStatus + CustIncome + TmWBank + OtherCC + AMBalance + UtilRate
    Distribution = Binomial

Estimated Coefficients:
                   Estimate       SE        tStat      pValue  
                   ________    ________    _______    _________

    (Intercept)    0.70262     0.063862     11.002    3.734e-28
    CustAge        0.57683      0.27064     2.1313     0.033062
    TmAtAddress     1.0653      0.55233     1.9287     0.053762
    ResStatus       1.4189      0.65162     2.1775     0.029441
    EmpStatus      0.89916      0.29217     3.0776     0.002087
    CustIncome     0.77506      0.21942     3.5323    0.0004119
    TmWBank         1.0826      0.26583     4.0727    4.648e-05
    OtherCC         1.1354      0.52827     2.1493     0.031612
    AMBalance      0.99315      0.32642     3.0425    0.0023459
    UtilRate       0.16723      0.55745    0.29999      0.76419


1200 observations, 1190 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 85.6, p-value = 1.25e-14
Open Live Script

Create a creditscorecard object using the CreditCardData.mat file to load the dataMissing with missing values. 

load CreditCardData.mat 
head(dataMissing,5)
    CustID    CustAge    TmAtAddress     ResStatus     EmpStatus    CustIncome    TmWBank    OtherCC    AMBalance    UtilRate    status
    ______    _______    ___________    ___________    _________    __________    _______    _______    _________    ________    ______

      1          53          62         <undefined>    Unknown        50000         55         Yes       1055.9        0.22        0   
      2          61          22         Home Owner     Employed       52000         25         Yes       1161.6        0.24        0   
      3          47          30         Tenant         Employed       37000         61         No        877.23        0.29        0   
      4         NaN          75         Home Owner     Employed       53000         20         Yes       157.37        0.08        0   
      5          68          56         Home Owner     Employed       53000         14         Yes       561.84        0.11        0   

fprintf('Number of rows: %d\n',height(dataMissing))
Number of rows: 1200

fprintf('Number of missing values CustAge: %d\n',sum(ismissing(dataMissing.CustAge)))
Number of missing values CustAge: 30

fprintf('Number of missing values ResStatus: %d\n',sum(ismissing(dataMissing.ResStatus)))
Number of missing values ResStatus: 40

Use creditscorecard with the name-value argument 'BinMissingData' set to true to bin the missing numeric or categorical data in a separate bin. 

sc = creditscorecard(dataMissing,'IDVar','CustID','BinMissingData',true);
sc = autobinning(sc);
disp(sc)
  creditscorecard with properties:

                GoodLabel: 0
              ResponseVar: 'status'
               WeightsVar: ''
                 VarNames: {'CustID'  'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'  'status'}
        NumericPredictors: {'CustAge'  'TmAtAddress'  'CustIncome'  'TmWBank'  'AMBalance'  'UtilRate'}
    CategoricalPredictors: {'ResStatus'  'EmpStatus'  'OtherCC'}
           BinMissingData: 1
                    IDVar: 'CustID'
            PredictorVars: {'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'}
                     Data: [1200×11 table]

Display and plot bin information for numeric data for 'CustAge' that includes missing data in a separate bin labelled <missing>. 

[bi,cp] = bininfo(sc,'CustAge');
disp(bi)
         Bin         Good    Bad     Odds       WOE       InfoValue 
    _____________    ____    ___    ______    ________    __________

    {'[-Inf,33)'}     69      52    1.3269    -0.42156      0.018993
    {'[33,37)'  }     63      45       1.4    -0.36795      0.012839
    {'[37,40)'  }     72      47    1.5319     -0.2779     0.0079824
    {'[40,46)'  }    172      89    1.9326    -0.04556     0.0004549
    {'[46,48)'  }     59      25      2.36     0.15424     0.0016199
    {'[48,51)'  }     99      41    2.4146     0.17713     0.0035449
    {'[51,58)'  }    157      62    2.5323     0.22469     0.0088407
    {'[58,Inf]' }     93      25      3.72     0.60931      0.032198
    {'<missing>'}     19      11    1.7273    -0.15787    0.00063885
    {'Totals'   }    803     397    2.0227         NaN      0.087112

plotbins(sc,'CustAge')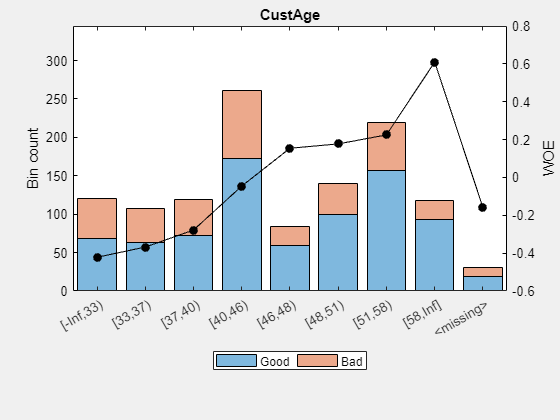

{"String":"Figure contains an axes object. The axes object with title CustAge contains 3 objects of type bar, line. These objects represent Good, Bad.","Tex":[],"LaTex":[]}

Display and plot bin information for categorical data for 'ResStatus' that includes missing data in a separate bin labelled <missing>. 

[bi,cg] = bininfo(sc,'ResStatus');
disp(bi)
         Bin          Good    Bad     Odds        WOE       InfoValue 
    ______________    ____    ___    ______    _________    __________

    {'Tenant'    }    296     161    1.8385    -0.095463     0.0035249
    {'Home Owner'}    352     171    2.0585     0.017549    0.00013382
    {'Other'     }    128      52    2.4615      0.19637     0.0055808
    {'<missing>' }     27      13    2.0769     0.026469    2.3248e-05
    {'Totals'    }    803     397    2.0227          NaN     0.0092627

plotbins(sc,'ResStatus')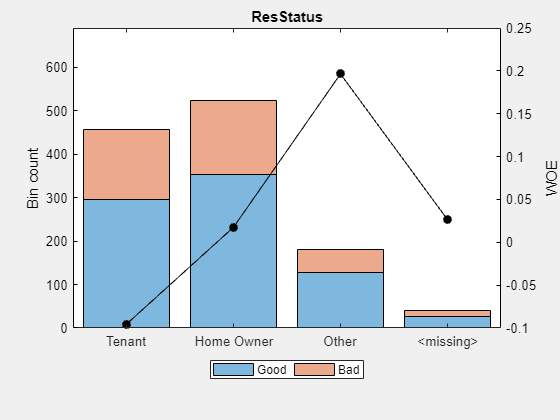

{"String":"Figure contains an axes object. The axes object with title ResStatus contains 3 objects of type bar, line. These objects represent Good, Bad.","Tex":[],"LaTex":[]}

Use fitmodel to fit a logistic regression model using Weight of Evidence (WOE) data. fitmodel internally transforms all the predictor variables into WOE values, using the bins found with the automatic binning process. fitmodel then fits a logistic regression model using a stepwise method (by default). For predictors that have missing data, there is an explicit <missing> bin, with a corresponding WOE value computed from the data. When using fitmodel, the corresponding WOE value for the <missing> bin is applied when performing the WOE transformation. For example, a missing value for customer age (CustAge) is replaced with -0.15787 which is the WOE value for the <missing> bin for the CustAge predictor. However, when 'BinMissingData' is false, a missing value for CustAge remains as missing (NaN) when applying the WOE transformation.

[sc,mdl] = fitmodel(sc);
1. Adding CustIncome, Deviance = 1490.8527, Chi2Stat = 32.588614, PValue = 1.1387992e-08
2. Adding TmWBank, Deviance = 1467.1415, Chi2Stat = 23.711203, PValue = 1.1192909e-06
3. Adding AMBalance, Deviance = 1455.5715, Chi2Stat = 11.569967, PValue = 0.00067025601
4. Adding EmpStatus, Deviance = 1447.3451, Chi2Stat = 8.2264038, PValue = 0.0041285257
5. Adding CustAge, Deviance = 1442.8477, Chi2Stat = 4.4974731, PValue = 0.033944979
6. Adding ResStatus, Deviance = 1438.9783, Chi2Stat = 3.86941, PValue = 0.049173805
7. Adding OtherCC, Deviance = 1434.9751, Chi2Stat = 4.0031966, PValue = 0.045414057

Generalized linear regression model:
    logit(status) ~ 1 + CustAge + ResStatus + EmpStatus + CustIncome + TmWBank + OtherCC + AMBalance
    Distribution = Binomial

Estimated Coefficients:
                   Estimate       SE       tStat       pValue  
                   ________    ________    ______    __________

    (Intercept)    0.70229     0.063959     10.98    4.7498e-28
    CustAge        0.57421      0.25708    2.2335      0.025513
    ResStatus       1.3629      0.66952    2.0356       0.04179
    EmpStatus      0.88373       0.2929    3.0172      0.002551
    CustIncome     0.73535       0.2159     3.406    0.00065929
    TmWBank         1.1065      0.23267    4.7556    1.9783e-06
    OtherCC         1.0648      0.52826    2.0156      0.043841
    AMBalance       1.0446      0.32197    3.2443     0.0011775


1200 observations, 1192 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 88.5, p-value = 2.55e-16

Input Arguments

collapse all

Credit scorecard model, specified as a creditscorecard object. Use creditscorecard to create a creditscorecard object.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: [sc,mdl] = fitmodel(sc,'VariableSelection','FullModel')

Predictor variables for fitting the creditscorecard object, specified as the comma-separated pair consisting of 'PredictorVars' and a cell array of character vectors. When provided, the creditscorecard object property PredictorsVars is updated. Note that the order of predictors in the original dataset is enforced, regardless of the order in which 'PredictorVars' is provided. When not provided, the predictors used to create the creditscorecard object (by using creditscorecard) are used.

Data Types: cell

The variable selection method to fit the logistic regression model, specified as the comma-separated pair consisting of 'VariableSelection' and a character vector with values 'Stepwise' or 'FullModel':

  • Stepwise — Uses a stepwise selection method which calls the Statistics and Machine Learning Toolbox™ function stepwiseglm. Only variables in PredictorVars can potentially become part of the model and uses the StartingModel name-value pair argument to select the starting model.

  • FullModel — Fits a model with all predictor variables in the PredictorVars name-value pair argument and calls fitglm.

Note

Only variables in the PredictorVars property of the creditscorecard object can potentially become part of the logistic regression model and only linear terms are included in this model with no interactions or any other higher-order terms.

The response variable is mapped so that “Good” is 1 and “Bad” is 0.

Data Types: char

Initial model for the Stepwise variable selection method, specified as the comma-separated pair consisting of 'StartingModel' and a character vector with values 'Constant' or 'Linear'. This option determines the initial model (constant or linear) that the Statistics and Machine Learning Toolbox function stepwiseglm starts with.

  • Constant — Starts the stepwise method with an empty (constant only) model.

  • Linear — Starts the stepwise method from a full (all predictors in) model.

Note

StartingModel is used only for the Stepwise option of VariableSelection and has no effect for the FullModel option of VariableSelection.

Data Types: char

Indicator to display model information at command line, specified as the comma-separated pair consisting of 'Display' and a character vector with value 'On' or 'Off'.

Data Types: char

Output Arguments

collapse all

Credit scorecard model, returned as an updated creditscorecard object. The creditscorecard object contains information about the model predictors and coefficients used to fit the WOE data. For more information on using the creditscorecard object, see creditscorecard.

Fitted logistic model, returned as an object of type GeneralizedLinearModel containing the fitted model. For more information on a GeneralizedLinearModel object, see GeneralizedLinearModel.

Note

When creating the creditscorecard object with creditscorecard, if the optional name-value pair argument WeightsVar was used to specify observation (sample) weights, then mdl uses the weighted counts with stepwiseglm and fitglm.

More About

collapse all

Using fitmodel with Weights

When observation weights are provided in the credit scorecard data, the weights are used to calibrate the model coefficients.

The underlying Statistics and Machine Learning Toolbox functionality for stepwiseglm and fitglm supports observation weights. The weights also affect the logistic model through the WOE values. The WOE transformation is applied to all predictors before fitting the logistic model. The observation weights directly impact the WOE values. For more information, see Using bininfo with Weights and Credit Scorecard Modeling Using Observation Weights.

Therefore, the credit scorecard points and final score depend on the observation weights through both the logistic model coefficients and the WOE values.

Models

A logistic regression model is used in the creditscorecard object.

For the model, the probability of being “Bad” is defined as: ProbBad = exp(-s) / (1 + exp(-s)).

References

[1] Anderson, R. The Credit Scoring Toolkit. Oxford University Press, 2007.

[2] Refaat, M. Credit Risk Scorecards: Development and Implementation Using SAS. lulu.com, 2011.

Version History

Introduced in R2014b

See Also

| | | | | | | | | | | | | | | | |

Topics