simulateNormalScenariosByData

Simulate multivariate normal asset return scenarios from data

Syntax

obj = simulateNormalScenariosByData(obj,AssetReturns)

obj = simulateNormalScenariosByData(obj,AssetReturns,NumScenarios,Name,Value)

Description

obj = simulateNormalScenariosByData(obj,AssetReturns) simulates multivariate normal asset return scenarios from data for portfolio object for PortfolioCVaR or PortfolioMAD objects. For details on the workflows, see PortfolioCVaR Object Workflow, and PortfolioMAD Object Workflow.

example

obj = simulateNormalScenariosByData(obj,AssetReturns,NumScenarios,Name,Value) simulates multivariate normal asset return scenarios from data for portfolio object for PortfolioCVaR or PortfolioMAD objects using additional options specified by one or more Name,Value pair arguments.

This function estimates the mean and covariance of asset returns from either price or return data and then uses these estimates to generate the specified number of scenarios with the function mvnrnd.

Data can be in a NumSamples-by-NumAssets matrix of NumSamples prices or returns at a given periodicity for a collection of NumAssets assets, a table or a timetable.

Note

If you want to use the method multiple times and you want to simulate identical scenarios each time the function is called, precede each function call with rng(seed) using a specified integer seed.

example

Examples

collapse all

Simulate Multivariate Normal Asset Return Scenarios from Data for a PortfolioCVaR Object

Open Live Script

Given a PortfolioCVaR object p, use the simulateNormalScenariosByData function to simulate multivariate normal asset return scenarios from data.

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];
m = m/12;
C = C/12;

RawData = mvnrnd(m, C, 240);
NumScenarios = 2000;

p = PortfolioCVaR;
p = simulateNormalScenariosByData(p, RawData, NumScenarios)

p = 
  PortfolioCVaR with properties:

                       BuyCost: []
                      SellCost: []
                  RiskFreeRate: []
              ProbabilityLevel: []
                      Turnover: []
                   BuyTurnover: []
                  SellTurnover: []
                  NumScenarios: 2000
                          Name: []
                     NumAssets: 4
                     AssetList: []
                      InitPort: []
                   AInequality: []
                   bInequality: []
                     AEquality: []
                     bEquality: []
                    LowerBound: []
                    UpperBound: []
                   LowerBudget: []
                   UpperBudget: []
                   GroupMatrix: []
                    LowerGroup: []
                    UpperGroup: []
                        GroupA: []
                        GroupB: []
                    LowerRatio: []
                    UpperRatio: []
                  MinNumAssets: []
                  MaxNumAssets: []
    ConditionalBudgetThreshold: []
        ConditionalUpperBudget: []
                     BoundType: []

p = setDefaultConstraints(p);
p = setProbabilityLevel(p, 0.9);

disp(p);

  PortfolioCVaR with properties:

                       BuyCost: []
                      SellCost: []
                  RiskFreeRate: []
              ProbabilityLevel: 0.9000
                      Turnover: []
                   BuyTurnover: []
                  SellTurnover: []
                  NumScenarios: 2000
                          Name: []
                     NumAssets: 4
                     AssetList: []
                      InitPort: []
                   AInequality: []
                   bInequality: []
                     AEquality: []
                     bEquality: []
                    LowerBound: [4x1 double]
                    UpperBound: []
                   LowerBudget: 1
                   UpperBudget: 1
                   GroupMatrix: []
                    LowerGroup: []
                    UpperGroup: []
                        GroupA: []
                        GroupB: []
                    LowerRatio: []
                    UpperRatio: []
                  MinNumAssets: []
                  MaxNumAssets: []
    ConditionalBudgetThreshold: []
        ConditionalUpperBudget: []
                     BoundType: [4x1 categorical]

Simulate Multivariate Normal Asset Return Scenarios from Data for `PortfolioCVaR` Object Using Financial Timetable Data

Open Live Script

To illustrate using the simulateNormalScenariosByData function with AssetReturns data continued in a timetable object, use the CAPMuniverse.mat which contains a timetable object (AssetTimeTable) for returns data.

load CAPMuniverse;
AssetsTimeTable.Properties

ans = 
  TimetableProperties with properties:

             Description: ''
                UserData: []
          DimensionNames: {'Time'  'Variables'}
           VariableNames: {'AAPL'  'AMZN'  'CSCO'  'DELL'  'EBAY'  'GOOG'  'HPQ'  'IBM'  'INTC'  'MSFT'  'ORCL'  'YHOO'  'MARKET'  'CASH'}
           VariableTypes: ["double"    "double"    "double"    "double"    "double"    "double"    "double"    "double"    "double"    "double"    "double"    "double"    "double"    "double"]
    VariableDescriptions: {}
           VariableUnits: {}
      VariableContinuity: []
                RowTimes: [1471x1 datetime]
               StartTime: 03-Jan-2000
              SampleRate: NaN
                TimeStep: NaN
                  Events: []
        CustomProperties: No custom properties are set.
      Use addprop and rmprop to modify CustomProperties.

head(AssetsTimeTable,5)

       Time          AAPL         AMZN         CSCO         DELL         EBAY       GOOG       HPQ          IBM         INTC         MSFT         ORCL         YHOO        MARKET         CASH   
    ___________    _________    _________    _________    _________    _________    ____    _________    _________    _________    _________    _________    _________    _________    __________

    03-Jan-2000     0.088805       0.1742     0.008775    -0.002353      0.12829    NaN       0.03244     0.075368      0.05698    -0.001627     0.054078     0.097784    -0.012143    0.00020522
    04-Jan-2000    -0.084331     -0.08324     -0.05608     -0.08353    -0.093805    NaN     -0.075613    -0.033966    -0.046667    -0.033802      -0.0883    -0.067368     -0.03166    0.00020339
    05-Jan-2000     0.014634     -0.14877    -0.003039     0.070984     0.066875    NaN     -0.006356      0.03516     0.008199     0.010567    -0.052837    -0.073363     0.011443    0.00020376
    06-Jan-2000    -0.086538    -0.060072    -0.016619    -0.038847    -0.012302    NaN     -0.063688    -0.017241     -0.05824    -0.033477    -0.058824     -0.10307     0.011743    0.00020266
    07-Jan-2000     0.047368     0.061013       0.0587    -0.037708    -0.000964    NaN      0.028416    -0.004386      0.04127     0.013091     0.076771      0.10609      0.02393    0.00020157

Notice that GOOG has missing data (NaN) because it was not listed before Aug 2004. The simulateNormalScenariosByData function has a name-value pair argument 'MissingData' that indicates with a Boolean value whether to use the missing data capabilities of Financial Toolbox™ software. The default value for 'MissingData' is false which removes all samples with NaN values. If, however, 'MissingData' is set to true, the estimateAssetMoments function uses the ECM algorithm to estimate asset moments. The simulateNormalScenariosByData function also accepts a name-value pair argument 'DataFormat' with a corresponding value set to 'prices' to indicate that the input to the function is in the form of asset prices and not returns (the default value for the 'DataFormat' argument is 'returns').

NumScenarios = 100;
r = PortfolioCVaR;
r = simulateNormalScenariosByData(r,AssetsTimeTable,NumScenarios,'DataFormat','Returns','MissingData',true);

In addition, simulateNormalScenariosByData extracts asset names or identifiers from a timetable object when the name-value argument 'GetAssetList' is set to true (its default value is false). If the 'GetAssetList' value is true, the timetable column identifiers are used to set the AssetList property of the PortfolioCVaR object. To show this, the formation of the PortfolioCVaR object r is repeated with the 'GetAssetList' flag set to true.

r = simulateNormalScenariosByData(r,AssetsTimeTable,NumScenarios,'GetAssetList',true);
disp(r.AssetList)

    {'AAPL'}    {'AMZN'}    {'CSCO'}    {'DELL'}    {'EBAY'}    {'GOOG'}    {'HPQ'}    {'IBM'}    {'INTC'}    {'MSFT'}    {'ORCL'}    {'YHOO'}    {'MARKET'}    {'CASH'}

Estimate Mean and Covariance of Asset Returns from Market Data for a PortfolioCVaR Object

Open Live Script

Create a PortfolioCVaR object p and use the simulateNormalScenariosByData function with market data loaded from CAPMuniverse.mat to simulate multivariate normal asset return scenarios. The market data, AssetsTimeTable, is a timetable of asset returns.

load CAPMuniverse

p = PortfolioCVaR('AssetList',Assets);
disp(p);

  PortfolioCVaR with properties:

                       BuyCost: []
                      SellCost: []
                  RiskFreeRate: []
              ProbabilityLevel: []
                      Turnover: []
                   BuyTurnover: []
                  SellTurnover: []
                  NumScenarios: []
                          Name: []
                     NumAssets: 14
                     AssetList: {'AAPL'  'AMZN'  'CSCO'  'DELL'  'EBAY'  'GOOG'  'HPQ'  'IBM'  'INTC'  'MSFT'  'ORCL'  'YHOO'  'MARKET'  'CASH'}
                      InitPort: []
                   AInequality: []
                   bInequality: []
                     AEquality: []
                     bEquality: []
                    LowerBound: []
                    UpperBound: []
                   LowerBudget: []
                   UpperBudget: []
                   GroupMatrix: []
                    LowerGroup: []
                    UpperGroup: []
                        GroupA: []
                        GroupB: []
                    LowerRatio: []
                    UpperRatio: []
                  MinNumAssets: []
                  MaxNumAssets: []
    ConditionalBudgetThreshold: []
        ConditionalUpperBudget: []
                     BoundType: []

Simulate the scenarios from the timetable data for each of the assets from CAPMuniverse.mat and plot the efficient frontier.

p = simulateNormalScenariosByData(p,AssetsTimeTable,10000,'missingdata',true);
p = setDefaultConstraints(p);
p = setProbabilityLevel(p, 0.9);
plotFrontier(p);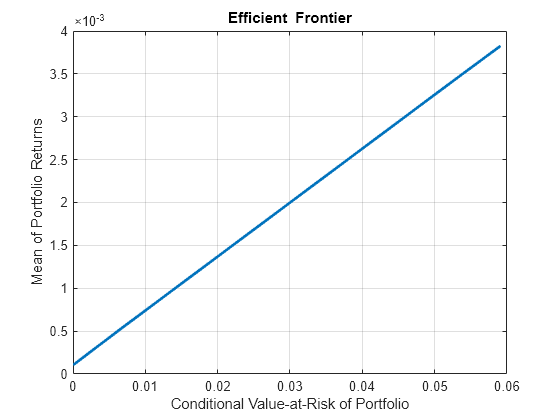

Figure contains an axes object. The axes object with title Efficient Frontier, xlabel Conditional Value-at-Risk of Portfolio, ylabel Mean of Portfolio Returns contains an object of type line. This object represents Efficient Frontier.

Estimate Mean and Covariance of Asset Returns from Data for a PortfolioMAD Object

Open Live Script

Given a PortfolioMAD object p, use the simulateNormalScenariosByData function to simulate multivariate normal asset return scenarios from data.

m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0; 
    0.00408 0.0289 0.0204 0.0119;
    0.00192 0.0204 0.0576 0.0336;
    0 0.0119 0.0336 0.1225 ];
m = m/12;
C = C/12;

RawData = mvnrnd(m, C, 240);
NumScenarios = 2000;

p = PortfolioMAD;
p = simulateNormalScenariosByData(p, RawData, NumScenarios);
p = setDefaultConstraints(p);

disp(p);

  PortfolioMAD with properties:

                       BuyCost: []
                      SellCost: []
                  RiskFreeRate: []
                      Turnover: []
                   BuyTurnover: []
                  SellTurnover: []
                  NumScenarios: 2000
                          Name: []
                     NumAssets: 4
                     AssetList: []
                      InitPort: []
                   AInequality: []
                   bInequality: []
                     AEquality: []
                     bEquality: []
                    LowerBound: [4x1 double]
                    UpperBound: []
                   LowerBudget: 1
                   UpperBudget: 1
                   GroupMatrix: []
                    LowerGroup: []
                    UpperGroup: []
                        GroupA: []
                        GroupB: []
                    LowerRatio: []
                    UpperRatio: []
                  MinNumAssets: []
                  MaxNumAssets: []
    ConditionalBudgetThreshold: []
        ConditionalUpperBudget: []
                     BoundType: [4x1 categorical]

Estimate Mean and Covariance of Asset Returns from Market Data for a PortfolioMAD Object

Open Live Script

Create a PortfolioMAD object p and use the simulateNormalScenariosByData function with market data loaded from CAPMuniverse.mat to simulate multivariate normal asset return scenarios. The market data, AssetsTimeTable, is a timetable of asset returns.

load CAPMuniverse

p = PortfolioMAD('AssetList',Assets);
disp(p.AssetList');

    {'AAPL'  }
    {'AMZN'  }
    {'CSCO'  }
    {'DELL'  }
    {'EBAY'  }
    {'GOOG'  }
    {'HPQ'   }
    {'IBM'   }
    {'INTC'  }
    {'MSFT'  }
    {'ORCL'  }
    {'YHOO'  }
    {'MARKET'}
    {'CASH'  }

Simulate the scenarios from the timetable data for each of the assets from CAPMuniverse.mat and plot the efficient frontier.

p = simulateNormalScenariosByData(p,AssetsTimeTable,10000,'missingdata',true);
p = setDefaultConstraints(p);
plotFrontier(p);

Figure contains an axes object. The axes object with title Efficient Frontier, xlabel Mean Absolute Deviation of Portfolio Returns, ylabel Mean of Portfolio Returns contains an object of type line. This object represents Efficient Frontier.

Input Arguments

collapse all

`obj` — Object for portfolio
object

Object for portfolio, specified using a PortfolioCVaR or PortfolioMAD object.

For more information on creating a PortfolioCVaR or PortfolioMAD object, see

Data Types: object

`AssetReturns` — Asset data that can be converted into asset returns
matrix | table | timetable

Asset data that can be converted into asset returns ([NumSamples-by-NumAssets] matrix), specified as a matrix, table, or timetable.

AssetReturns data can be:

NumSamples-by-NumAssets matrix.
Table of NumSamples prices or returns at a given periodicity for a collection of NumAssets assets
Timetable object with NumSamples observations and NumAssets time series

Data Types: double | table | timetable

`NumScenarios` — Number of scenarios to simulate
positive integer

Number of scenarios to simulate, specified as a positive integer.

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: p = simulateNormalScenariosByData(p,RawData,NumScenarios,'DataFormat','Returns','MissingData',true,'GetAssetList',true)

`DataFormat` — Flag to convert input data as prices into returns
`'Returns'` (default) | character vector with values `'Returns'` or `'Prices'`

Flag to convert input data as prices into returns, specified as the comma-separated pair consisting of 'DataFormat' and a character vector with the values:

'Returns' — Data in AssetReturns contains asset total returns.
'Prices' — Data in AssetReturns contains asset total return prices.

Data Types: char

`MissingData` — Flag to use ECM algorithm to handle `NaN` values
`false` (default) | logical with values `true` or `false`

Flag to use ECM algorithm to handle NaN values, specified as the comma-separated pair consisting of 'MissingData' and a logical with a value of true or false.

false — Do not use ECM algorithm to handle NaN values (exclude NaN values).
true — Use ECM algorithm to handle NaN values.

Data Types: logical

`GetAssetList` — Flag indicating which asset names to use for the asset list
`false` (default) | logical with values `true` or `false`

Flag indicating which asset names to use for the asset list, specified as the comma-separated pair consisting of 'GetAssetList' and a logical with a value of true or false.

false — Do not extract or create asset names.
true — Extract or create asset names from the table or timetable.

If a table or timetable is passed into this function using the AssetReturns argument and the GetAssetList flag is true, the column names from the table or timetable are used as asset names in obj.AssetList.

If a matrix is passed and the GetAssetList flag is true, default asset names are created based on the AbstractPortfolio property defaultforAssetList, which is 'Asset'.

If the GetAssetList flag is false, no action occurs, which is the default behavior.

Data Types: logical

Output Arguments

collapse all

`obj` — Updated portfolio object
object for portfolio

Updated portfolio object, returned as a PortfolioCVaR or PortfolioMAD object. For more information on creating a portfolio object, see

Tips

You can also use dot notation to simulate multivariate normal asset return scenarios from data for a PortfolioCVaR or PortfolioMAD object.

obj = obj.simulateNormalScenariosByData(AssetReturns,NumScenarios,Name,Value);

Version History

Introduced in R2012b

expand all

R2023a: `fints` support for `AssetReturns` argument removed

The AssetReturns argument no longer supports a fints object as a datatype.

simulateNormalScenariosByData

Syntax

Description

Examples

Simulate Multivariate Normal Asset Return Scenarios from Data for a PortfolioCVaR Object

Simulate Multivariate Normal Asset Return Scenarios from Data for `PortfolioCVaR` Object Using Financial Timetable Data

Estimate Mean and Covariance of Asset Returns from Market Data for a PortfolioCVaR Object

Estimate Mean and Covariance of Asset Returns from Data for a PortfolioMAD Object

Estimate Mean and Covariance of Asset Returns from Market Data for a PortfolioMAD Object

Input Arguments

`obj` — Object for portfolio
object

`AssetReturns` — Asset data that can be converted into asset returns
matrix | table | timetable

`NumScenarios` — Number of scenarios to simulate
positive integer

Name-Value Arguments

`DataFormat` — Flag to convert input data as prices into returns
`'Returns'` (default) | character vector with values `'Returns'` or `'Prices'`

`MissingData` — Flag to use ECM algorithm to handle `NaN` values
`false` (default) | logical with values `true` or `false`

`GetAssetList` — Flag indicating which asset names to use for the asset list
`false` (default) | logical with values `true` or `false`

Output Arguments

`obj` — Updated portfolio object
object for portfolio

Tips

Version History

R2023a: `fints` support for `AssetReturns` argument removed

See Also

Topics

External Websites

simulateNormalScenariosByData

Syntax

Description

Examples

Simulate Multivariate Normal Asset Return Scenarios from Data for a PortfolioCVaR Object

Simulate Multivariate Normal Asset Return Scenarios from Data for PortfolioCVaR Object Using Financial Timetable Data

Estimate Mean and Covariance of Asset Returns from Market Data for a PortfolioCVaR Object

Estimate Mean and Covariance of Asset Returns from Data for a PortfolioMAD Object

Estimate Mean and Covariance of Asset Returns from Market Data for a PortfolioMAD Object

Input Arguments

obj — Object for portfolio object

AssetReturns — Asset data that can be converted into asset returns matrix | table | timetable

NumScenarios — Number of scenarios to simulate positive integer

Name-Value Arguments

DataFormat — Flag to convert input data as prices into returns 'Returns' (default) | character vector with values 'Returns' or 'Prices'

MissingData — Flag to use ECM algorithm to handle NaN values false (default) | logical with values true or false

GetAssetList — Flag indicating which asset names to use for the asset list false (default) | logical with values true or false

Output Arguments

obj — Updated portfolio object object for portfolio

Tips

Version History

R2023a: fints support for AssetReturns argument removed

See Also

Topics

External Websites

Simulate Multivariate Normal Asset Return Scenarios from Data for `PortfolioCVaR` Object Using Financial Timetable Data

`obj` — Object for portfolio
object

`AssetReturns` — Asset data that can be converted into asset returns
matrix | table | timetable

`NumScenarios` — Number of scenarios to simulate
positive integer

`DataFormat` — Flag to convert input data as prices into returns
`'Returns'` (default) | character vector with values `'Returns'` or `'Prices'`

`MissingData` — Flag to use ECM algorithm to handle `NaN` values
`false` (default) | logical with values `true` or `false`

`GetAssetList` — Flag indicating which asset names to use for the asset list
`false` (default) | logical with values `true` or `false`

`obj` — Updated portfolio object
object for portfolio

R2023a: `fints` support for `AssetReturns` argument removed