火花塞发动机扭矩动力学的神经状态空间模型

此示例使用:

此示例使用神经状态空间模型描述了火花点火 (SI) 发动机的非线性扭矩动力学的降阶建模 (ROM)。所确定的模型可用于硬件在环 (HIL) 测试、动力系统控制、诊断和训练算法设计。例如，您可以使用该模型进行后处理控制和诊断算法开发。有关神经状态空间模型的详细信息，请参阅Neural State-Space Models。

您可以使用系统输入和输出的测量来辨识模型。这些数据可以来自对真实发动机或高保真模型的测量，例如使用 Powertrain Blockset™ SI 参考应用程序创建的模型。

数据准备

加载并显示发动机数据时间表。

load SIEngineData IOData
stackedplot(IOData)
title('SI Engine Signals')

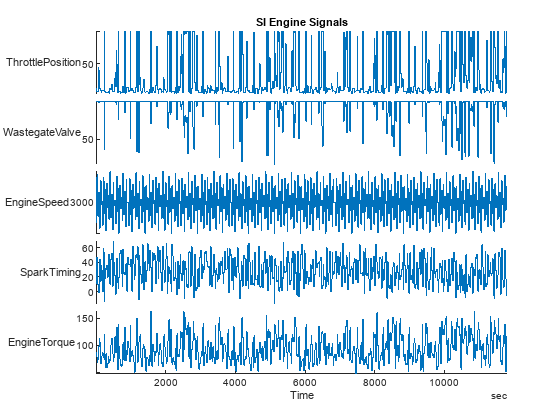
该时间表包含以 10 Hz 测量的五个变量的十万多个观测值。

节气门位置（度）
废气旁通阀面积（开度百分比）
发动机转速 (RPM)
火花正时（度）
发动机扭矩 (N m)

使数据归一化。

IODataN = normalize(IOData);

将数据分为估计（前 60000 个数据点）和验证（剩余数据点）部分。

eData = IODataN(1:6e4,:);     % portion used for estimation
vData = IODataN(6e4+1:end,:); % portion used for validation

将训练数据下采样 10 倍。这有助于加快模型训练过程，并将拟合的重点限制在较低的频率区域。

% Downsample datasets 10 times
eDataD = idresamp(eData,[1 10]); 
vDataD = idresamp(vData,[1 10]);
eDataD.Properties.TimeStep

ans = duration
   1 sec

height(eDataD)

ans = 6000

模型训练目标是生成一个以发动机扭矩为输出，其他四个变量为输入的动态系统。

神经状态空间模型辨识

关于神经状态空间模型

神经状态空间模型是一种非线性状态空间模型，其中状态转换和测量函数使用神经网络建模。在 System Identification Toolbox™ 中，它们由 idNeuralStateSpace 对象表示。非线性状态空间模型具有以下形式：

$\begin{array}{l} \dot{x} = f (x, u, t, θ_{1}) \\ y = g (x, u, t, θ_{2}) \end{array}$

这里 $x (t)$ 是状态变量， $u (t)$ 是输入， $y (t)$ 是输出。通常，没有明确的时间依赖性，因此方程可以简化为：

$\begin{array}{l} \dot{x} = f (x, u, θ_{1}) \\ y = g (x, u, θ_{2}) \end{array}$

此外，如果没有外生输入，方程进一步简化为：

$\begin{array}{l} \dot{x} = f (x, θ_{1}) \\ y = g (x, θ_{2}) \end{array}$

这里， $f (\cdot)$ 和 $g (\cdot)$ 是多层前馈网络，通常由 Deep Network Toolbox™ 的 dlnetwork 对象描述。 $θ_{1}$ 和 $θ_{2}$ 是可辨识参数，由与这些网络的每一层相关的权重和偏置组成。nlssest 命令可用于训练 $f (\cdot)$ 和 $g (\cdot)$ 网络（即估计参数 $θ_{1}$ 和 $θ_{2}$ 的值）。训练需要直接测量模型的状态。因此，一部分输出是状态变量，函数 $g (\cdot)$ 是前 $n_{x}$ 个输出的恒等函数，其中 $n_{x} : = \dim (x)$ 。

模型训练

训练神经状态空间模型需要通过设置输入/输出和状态维度以及网络 $f (\cdot)$ 和 $g (\cdot)$ 的类型来配置模型结构。在此示例中，您将训练具有四个输入的单状态 ( $n_{x} = 1$ ) 模型。状态变量是发动机扭矩。它是直接测量的，因此也被视为模型输出。因此，该模型有一个输出 ( $y (t) = x (t)$ )。

首先从 eData 时间表中的变量列表中指定输入和输出信号。

Inputs = ["ThrottlePosition","WastegateValve","EngineSpeed","SparkTiming"];
Output = "EngineTorque";

使用 idNeuralStateSpace 构造函数创建神经状态空间模型。

% Define a neural state-space model
nx = 1; % number of states = number of outputs
nssModel = idNeuralStateSpace(nx,NumInputs=4); 
nssModel.InputName = Inputs;
nssModel.OutputName = Output;

% Configure the state network f()
nssModel.StateNetwork = createMLPNetwork(nssModel,"state", ...
    LayerSizes=[128 128], ...
    WeightsInitializer="glorot", ...
    BiasInitializer="zeros", ...
    Activations='tanh')

Continuous-time Neural ODE in 1 variables
     dx/dt = f(x(t),u(t))
      y(t) = x(t) + e(t)

f(.) network:
  Deep network with 2 fully connected, hidden layers
  Activation function: Tanh
g(.) network:
  Deep network with 0 fully connected, hidden layers
  Activation function: 

Variables: x1

Status:                                                         
Created by direct construction or transformation. Not estimated.
More information in model's "Report" property.

Model Properties

接下来，准备数据和训练算法选项。数据已经被分割、下采样和归一化。现在，您可以通过将数据集 eDataD 分成重叠的段来创建多个数据试验进行训练。这样做可以有效地将预测范围从原始数据长度 (6000) 减少到各个段的长度。这种减少有时可以产生更具普遍性的结果。

predictionStep = 20; % length of each data segment
numExperiment = height(eDataD) - predictionStep;
Expts = cell(1, numExperiment); 

for i = 1:numExperiment
    Expts{i} = eDataD(i:i+predictionStep,:);
    if i>1
       % set the row time of each segment to be identical; this is a requirement for training a
       % neural state-space model with multiple data experiments
       Expts{i}.Properties.RowTimes = Expts{1}.Properties.RowTimes;
    end
end

使用 nssTrainingOptions 命令创建训练选项集。选择 Adam 作为训练求解器。设置最大训练次数和数据插值方法。

StateOpt = nssTrainingOptions('adam');
StateOpt.MaxEpochs = 90;
StateOpt.InputInterSample = 'pchip';

通过提供训练数据试验 (Expts) 和训练选项 (StateOpt)，使用 nlssest 命令更新神经状态空间模型 nssModel 的可学习参数。请注意，测量函数 $g (x, u, θ_{2}) = x (t)$ 不包含任何可学习的参数。

% Train the neural state-space model
tic
nssModel = nlssest(Expts,nssModel,StateOpt)

Training in progress (completed epoch/max epochs):        0/      90       1/      90       2/      90       3/      90       4/      90       5/      90       6/      90       7/      90       8/      90       9/      90      10/      90      11/      90      12/      90      13/      90      14/      90      15/      90      16/      90      17/      90      18/      90      19/      90      20/      90      21/      90      22/      90      23/      90      24/      90      25/      90      26/      90      27/      90      28/      90      29/      90      30/      90      31/      90      32/      90      33/      90      34/      90      35/      90      36/      90      37/      90      38/      90      39/      90      40/      90      41/      90      42/      90      43/      90      44/      90      45/      90      46/      90      47/      90      48/      90      49/      90      50/      90      51/      90      52/      90      53/      90      54/      90      55/      90      56/      90      57/      90      58/      90      59/      90      60/      90      61/      90      62/      90      63/      90      64/      90      65/      90      66/      90      67/      90      68/      90      69/      90      70/      90      71/      90      72/      90      73/      90      74/      90      75/      90      76/      90      77/      90      78/      90      79/      90      80/      90      81/      90      82/      90      83/      90      84/      90      85/      90      86/      90      87/      90      88/      90      89/      90

      90/      90

Generating estimation report...done.
Continuous-time Neural ODE in 1 variables
     dx/dt = f(x(t),u(t))
      y(t) = x(t) + e(t)

f(.) network:
  Deep network with 2 fully connected, hidden layers
  Activation function: Tanh
g(.) network:
  Deep network with 0 fully connected, hidden layers
  Activation function: 

Variables: x1

Status:                                                                                                        
Estimated using NLSSEST on time domain data "Expts".                                                           
Fit to estimation data: [-44.21 -49.85 -57.25 -67.86 -83.07 -105.3 -142.1 -272.2 -313.2 -27.87....%            
FPE: 0.01088, MSE: [0.008885 0.009086 0.009231 0.009365 0.009495 0.009436 0.009204 0.009095 0.009087 0.00869...
More information in model's "Report" property.

Model Properties

toc

Elapsed time is 2185.697275 seconds.

结果验证

运行比较命令，将模型的仿真响应与估计数据集 (eDataD) 和验证数据集 (vDataD) 进行比较。请注意，虽然该模型是在 20 个采样长的片段上进行训练的（有效地将预测范围缩小到 20），但它可以通过运行完整的仿真（范围约为 6000）进行验证。

clf
subplot(211)
compare(eDataD,nssModel)  % compare against estimation data
title('Neural State-Space Model: Comparison to Estimation Data')
subplot(212)
compare(vDataD,nssModel)  % compare against validation data
title('Comparison to Validation Data (Downsampled)')

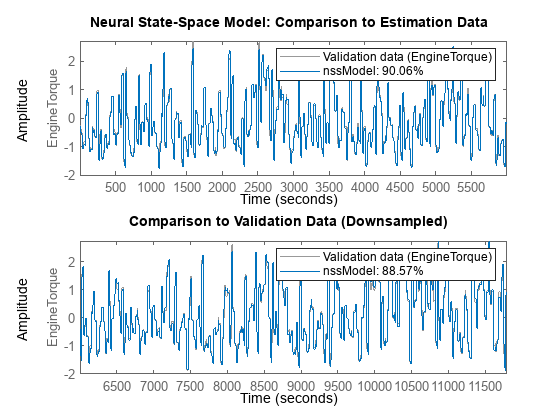
请注意，已经在下采样数据集上进行了训练和验证。您还可以使用原始采样时间为 0.1 秒的数据集来验证质量。这可以通过再次使用比较命令来完成，如下所示：

clf
compare(vData,nssModel)  % compare against original validation data (sample rate of 10 Hz)
title('Comparison to Original Validation Data (10 Hz)')

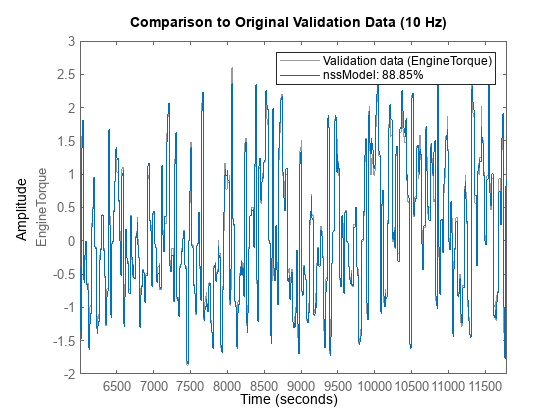
之所以能够进行比较，是因为模型 nssModel 是一个连续时间模型，可以与任何采样率的参考数据集进行比较。验证图显示辨识模型的质量良好。

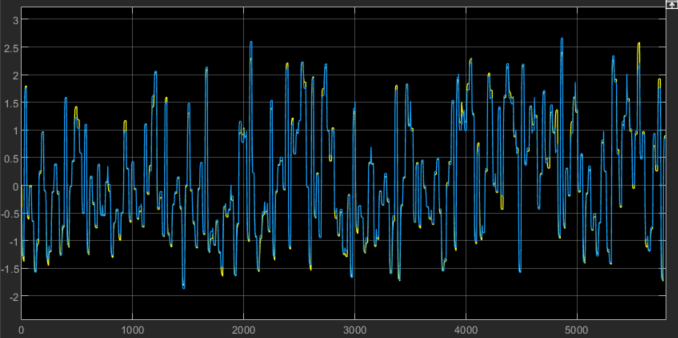
您还可以使用 MATLAB® 中的 sim 命令进行纯仿真，或使用专用 Neural SS Model 模块将其放入 Simulink® 模型中来验证模型质量。

% Create an iddata representation of the data in vData to feed the signals to the Simulink
% model using an IDDATA Source block.
zsim = iddata(vData,InputName=Inputs,OutputName=Output);
zsim.Tstart = 0;

% Open the simulation model and simulate it using zsim as the source of input data. 
mdl = 'nlss_simulator';
tstop = zsim.SamplingInstants(end);
Ts = zsim.Ts;
open_system(mdl)

sim(mdl);

另请参阅