探查来自具有各向异性体素间距的三维图像体的切片
此示例说明如何显示一个各向异性三维 MRI 数据体的切片。在各向异性图像体中,体素或三维体像素之间的间距在空间维度之间变化。例如,如果将一个 1×1×1 体素映射到世界坐标系中的一个 1×1×2 mm 区域,则体素间距是各向异性的。默认情况下,Image Processing Toolbox™ 函数以体素单位显示图像,并假设间距在世界坐标系中是一致的。因此,各向异性三维体可能会出现失真。
在此示例中,您应用两种方法沿每个维度显示切片,而不出现畸变:
Medical Imaging Toolbox™ 扩展了 Image Processing Toolbox™ 的功能以自动管理体素坐标系、世界坐标系和解剖坐标系之间的空间参照。要了解详细信息,请参阅Choose Approach for Medical Image Visualization (Medical Imaging Toolbox)。
加载 MRI 数据
加载一个包含数值数组 D 和灰度颜色图 map 的 MRI 数据集。数值数组包含 MRI 图像数据。体素间距是各向异性的,在世界坐标系中,横向切片比冠状切片和矢状切片厚 2.5 倍。您可以使用颜色图以足够的对比度显示三维体。使用 squeeze 函数删除单一维度。
load mri
DTransverse = squeeze(D);应用显示设置
在本节中,您将使用显示函数名称-值参量以无畸变方式显示 MRI 数据体。这些名称-值参量仅更新显示的纵横比,而不修改底层图像数据。当您不想使用插值修改数据的原始强度值时,仅调整显示是有益的。这种方法的一个限制是每次显示三维体时都必须设置名称-值参量。此外,一些函数(如 montage)没有用于缩放各向异性三维体的参量。
显示正交切片
使用 orthosliceViewer 对象显示正交切片平面。指定 ScaleFactors 名称-值参量以将 2.5 缩放因子应用于第三个维度。每个切片视图包括十字准线,可用于导航三维体。要导航切片,请在一个十字准线坐标系上暂停,直到光标变为十字四向箭头 ![]() ,然后点击并拖到新位置。其他切片视图会自动更新。
,然后点击并拖到新位置。其他切片视图会自动更新。
figure orthosliceViewer(DTransverse,ScaleFactors=[1 1 2.5]);

显示一叠切片
使用 sliceViewer 对象显示一叠可滚动的切片。默认情况下,sliceViewer 显示沿第三个维度的切片。在此示例中,前两个维度中的体素间距是相等的,因此二维切片不会出现畸变。
sliceViewer(DTransverse,Parent=figure);
title("Transverse Slices")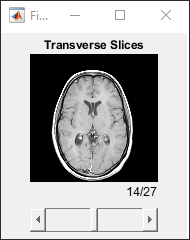
分别使用 SliceDirection 和 ScaleFactors 名称-值参量更改切片方向和应用缩放因子。通过将切片方向指定为 "X" 并将第三个维度的缩放因子指定为 2.5,显示一叠矢状切片。
sliceViewer(DTransverse,SliceDirection="X",ScaleFactors=[1 1 2.5],Parent=figure); title("Sagittal Slices")

将切片显示为三维对象
使用具有 SlicePlanes 渲染样式的 volshow 函数以三维方式显示切片。要以无畸变方式显示各向异性体素,请将 Transformation 名称-值参量指定为 affinetform3d 对象,该对象在第三个维度中以 2.5 的因子缩放三维体。点击并拖动一个切片以沿该轴在切片之间导航。要将三维体旋转至期望的方向,请点击图窗窗口中的任意空白区域并拖动。要将视图吸附到特定切片平面,请点击查看器左下角的轴指示图上的 X、Y 或 Z 标签。
sx = 1;
sy = 1;
sz = 2.5;
A = [sx 0 0 0; 0 sy 0 0; 0 0 sz 0; 0 0 0 1];
tform = affinetform3d(A);
vol = volshow(DTransverse,renderingStyle="SlicePlanes",Transformation=tform);
您还可以使用 Cinematic 渲染样式,通过高级光照将三维体作为三维对象进行查看。
vol = volshow(DTransverse,renderingStyle="CinematicRendering",Transformation=tform);
使用三维体查看器探索切片和三维体
使用 三维体查看器 以交互方式探索图像三维体。使用 volumeViewer 函数启动 App。要正确显示各向异性体素,请指定 ScaleFactors 名称-值参量。
volumeViewer(DTransverse,ScaleFactors=[1 1 2.5])
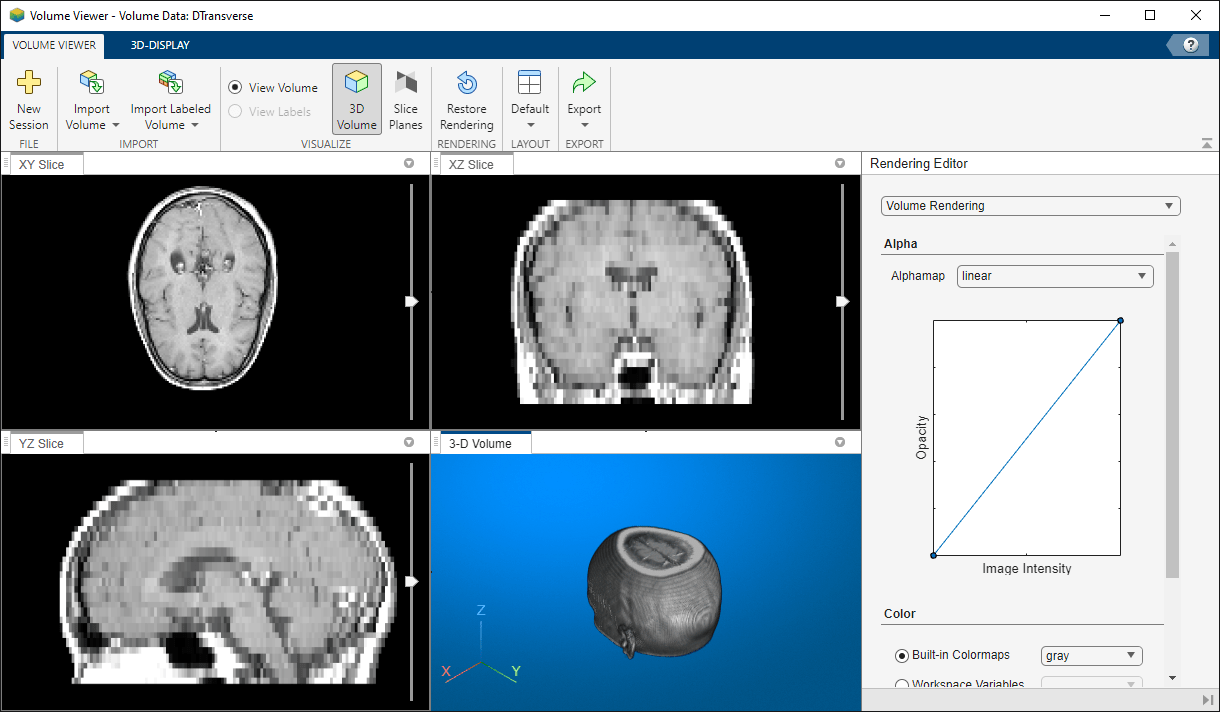
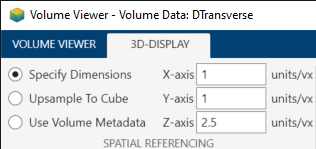
您也可以在 App 中指定缩放因子。在 App 工具条的三维显示选项卡中,在空间参照下,输入每个轴的缩放因子值。当您输入值时,值左侧的选项会自动更改为指定维度。
变换图像数据
在本节中,您将在显示图像三维体之前使用重采样和几何变换对其进行修改。重采样将各向异性体素网格插值到各向同性网格,后者显示图像而无缩放畸变。您也可以旋转三维体或应用其他几何变换以按约定的期望显示定向三维体。这种方法的一个好处是每次显示三维体时不需要指定名称-值参量。此外,这种方法使您能够使用诸如 montage 之类的函数,这些函数不支持使用名称-值参量来更改默认缩放或切片方向。
对三维体进行重采样以设置各向同性体素间距
使用 imresize3 函数将原始三维体重采样到一个各向同性体素网格中。使用缩放因子 2.5 计算各向同性三维体的目标切片数。
numSlices = round(2.5*size(DTransverse,3)); DTransverseIsotropic = imresize3(DTransverse,[128 128 numSlices]);
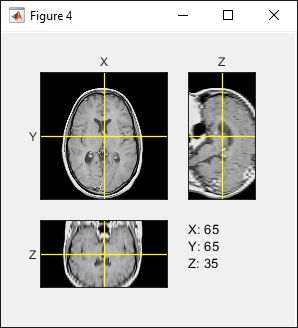
您可以使用显示函数精确显示重采样的三维体,而不应用缩放因子。使用不带 ScaleFactors 名称-值参量的 orthoSliceViewer 显示重采样的三维体。
figure orthosliceViewer(DTransverseIsotropic);
以蒙太奇方式显示定向图片
montage 函数将图像三维体显示为一叠沿第三个维度的切片。本节显示如何修改图像数据,以沿所有三个维度,在每个解剖学平面的理想方向上查看切片。
显示重采样的横向三维体的切片。应用颜色图 map 以足够的对比度显示图像。
figure montage(DTransverseIsotropic,map)

title("Transverse Slices")要以矢状切片堆叠形式查看三维体,请对 DTransverseIsotropic 的维度进行重新排序。
DSagittal = permute(DTransverseIsotropic,[1 3 2]);
旋转三维体以匹配矢状切片的理想方向,头部顶端位于图像的顶部,头部的前侧位于图像的左侧。
DSagittalRotated = imrotate3(DSagittal,90,[0 0 1],"cubic");以蒙太奇方式显示矢状切片。包括颜色图以设置显示范围。使用 Indices 名称-值参量显示切片 20 到 100 以排除空切片。
figure
montage(DSagittalRotated,map,Indices=20:100)
title("Sagittal Slices")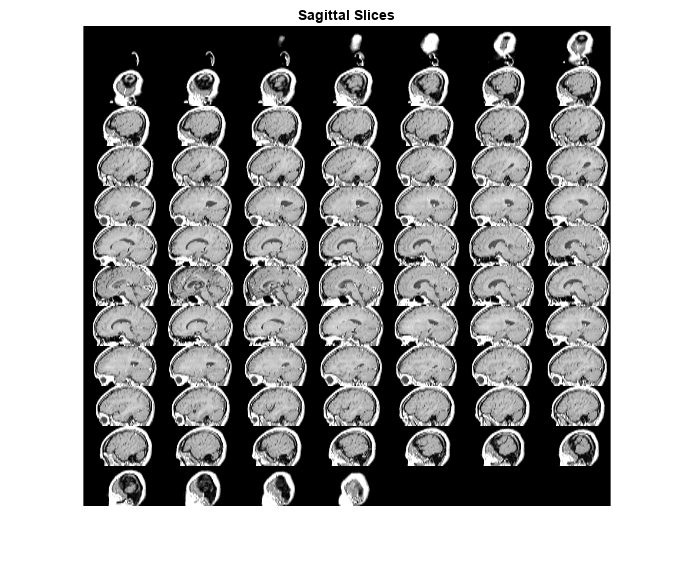
要以冠状切片堆叠形式查看三维体,请对 DTransverseIsotropic 的维度进行重新排序。
DCoronal = permute(DTransverseIsotropic,[2 3 1]);
旋转三维体以匹配冠状切片的理想方向,头部顶端位于图像的顶部,头部的左侧位于图像的左侧。
DCoronalRotated = imrotate3(DCoronal,90,[0 0 1],"cubic");以蒙太奇方式显示冠状切片。包括颜色图以设置显示范围。使用 Indices 名称-值参量显示切片 17 到 127 以排除空切片。
figure
montage(DCoronalRotated,map,Indices=17:127)
title("Coronal Slices")
另请参阅
三维体查看器 | 医学图像标注器 (Medical Imaging Toolbox) | sliceViewer | orthosliceViewer | volshow | imresize3 | imrotate3