中立型 DDE
以下示例说明如何使用 ddensd 求解中立型 DDE(时滞微分方程),其中时滞出现在导数项中。此问题最初由 Paul [1] 提出。
方程是:
.
在 时,历史解函数是 。
由于该方程在 项中存在时滞,因此该方程称为中立型 DDE。如果时滞仅出现在 项中,则根据时滞的形式,方程将是常时滞或状态相关 DDE。
要在 MATLAB® 中求解此方程,您需要先编写方程、时滞和历史解的代码,然后再调用时滞微分方程求解器 ddensd。您可以将这些作为局部函数包含在文件末尾(如本处所示),或者将它们作为单独的文件保存在 MATLAB 路径上的目录中。
编写时滞代码
首先,编写函数来定义方程中的时滞。方程中具有时滞的首项是 。
function dy = dely(t,y) dy = t/2; end
方程中具有时滞的另一个项是 。
function dyp = delyp(t,y) dyp = t-pi; end
在此示例中, 和 分别仅有一个时滞。如果有更多时滞,则您可以将它们添加到这些相同的函数文件中,这样函数将返回向量而不是标量。
注意:所有函数都作为局部函数包含在示例的末尾。
编写方程代码
现在,创建一个函数来编写方程代码。此函数应具有签名 yp = ddefun(t,y,ydel,ypdel),其中:
t是时间(自变量)。y是解(因变量)。ydel包含 的时滞。ypdel包含 的时滞。
求解器会自动将这些输入传递给该函数,但是变量名称决定如何编写方程代码。在这种情况下:
ydelypdel
function yp = ddefun(t,y,ydel,ypdel) yp = 1 + y - 2*ydel^2 - ypdel; end
编写历史解代码
接下来,创建一个函数来定义历史解。历史解是时间 的解。
function y = history(t) y = cos(t); end
求解方程
最后,定义积分区间 并使用 ddensd 求解器对 DDE 求解。
tspan = [0 pi]; sol = ddensd(@ddefun, @dely, @delyp, @history, [0,pi]);
对解进行绘图
解结构体 sol 具有字段 sol.x 和 sol.y,这两个字段包含求解器在这些时间点所用的内部时间步和对应的解。但是,您可以使用 deval 计算在特定点的解。
在 0 和 pi 之间以 20 个等间距点计算解。
tn = linspace(0,pi,20); yn = deval(sol,tn);
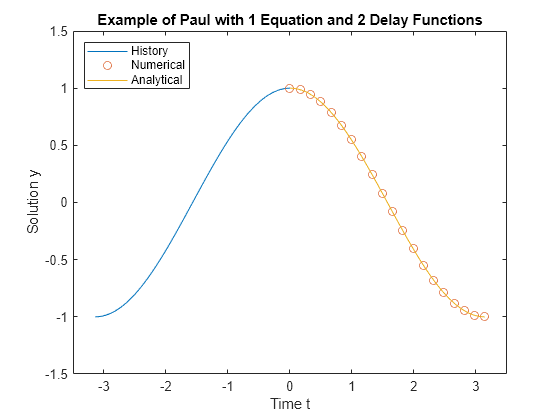
绘制计算解和历史解对解析解的图。
th = linspace(-pi,0); yh = history(th); ta = linspace(0,pi); ya = cos(ta); plot(th,yh,tn,yn,'o',ta,ya) legend('History','Numerical','Analytical','Location','NorthWest') xlabel('Time t') ylabel('Solution y') title('Example of Paul with 1 Equation and 2 Delay Functions') axis([-3.5 3.5 -1.5 1.5])
局部函数
此处列出了 DDE 求解器 ddensd 为计算解而调用的局部辅助函数。您也可以将这些函数作为它们自己的文件保存在 MATLAB 路径上的目录中。
function yp = ddefun(t,y,ydel,ypdel) % equation being solved yp = 1 + y - 2*ydel^2 - ypdel; end %------------------------------------------- function dy = dely(t,y) % delay for y dy = t/2; end %------------------------------------------- function dyp = delyp(t,y) % delay for y' dyp = t-pi; end %------------------------------------------- function y = history(t) % history function for t < 0 y = cos(t); end %-------------------------------------------
参考
[1] Paul, C.A.H.“A Test Set of Functional Differential Equations.”Numerical Analysis Reports.No. 243.Manchester, UK:Math Department, University of Manchester, 1994.
另请参阅
ddensd | ddesd | dde23 | deval