deconv
最小二乘反卷积和多项式除法
说明
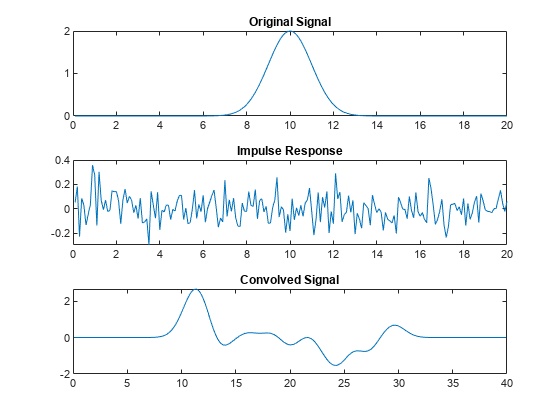
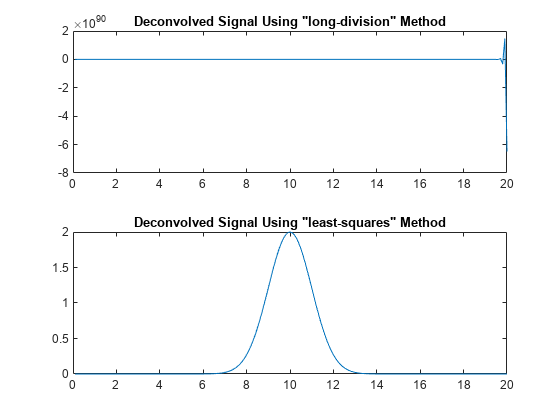
多项式长除法
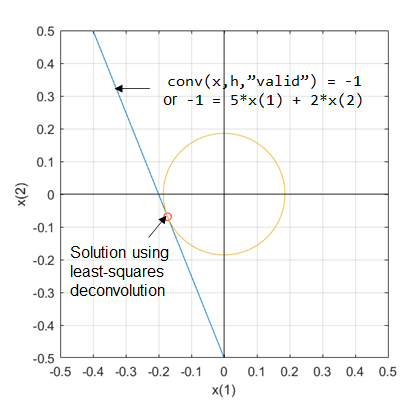
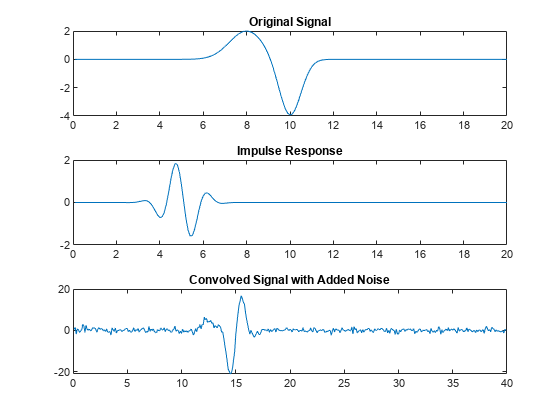
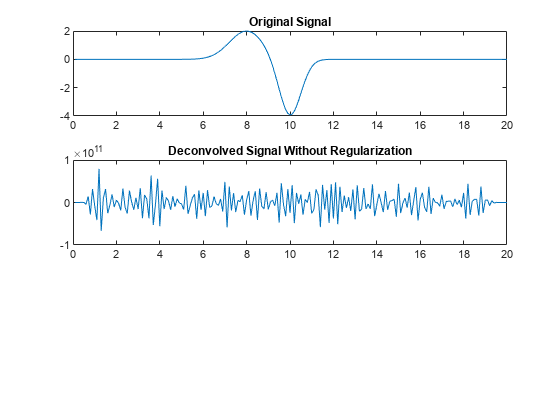
最小二乘反卷积
自 R2023b 起
[ 支持上述语法中的任何输入参量组合，且可使用一个或多个名称-值参量指定选项。x,r] = deconv(___,Name=Value)
您可以使用
deconv(__,Method=algorithm)指定反卷积方法，其中algorithm可以是"long-division"或"least-squares"。您还可以使用
deconv(__,RegularizationFactor=alpha)将吉洪诺夫正则化因子指定为反卷积方法的最小二乘解。
示例
创建两个向量 y 和 h，分别包含多项式 和 的系数。通过对 y 进行反卷积以消除 h ，将第一个多项式除以第二个多项式。反卷积得出与多项式 对应的商系数以及与 对应的余数系数。
y = [2 7 4 9]; h = [1 0 1]; [x,r] = deconv(y,h)
x = 1×2
2 7
r = 1×4
0 0 2 2
自 R2023b 起
创建一个具有高斯形状的信号 x。将此信号与包含随机噪声的冲激响应 h 求卷积。
N = 200;
n = 0.1*(1:N);
rng("default")
x = 2*exp(-0.5*((n-10)).^2);
h = 0.1*randn(1,length(x));
y = conv(x,h);绘制原始信号、冲激响应和卷积信号。
figure tiledlayout(3,1) nexttile plot(n,x) title("Original Signal") nexttile plot(n,h) title("Impulse Response") nexttile plot(0.1*(1:length(y)),y) title("Convolved Signal")
接下来，使用默认多项式长除法方法，求出信号 y 关于冲激响应 h 的反卷积。使用这种方法时，反卷积计算不稳定，结果可以迅速增大。
[x1,r1] = deconv(y,h); x1(end)
ans = 7.5992e+90
相反，使用最小二乘法求反卷积会执行数值稳定的计算。
[x2,r2] = deconv(y,h,Method="least-squares");绘制两个反卷积结果。此处，最小二乘法正确地返回了具有高斯形状的原始信号。
figure tiledlayout(2,1) nexttile plot(n,x1) title("Deconvolved Signal Using ""long-division"" Method") nexttile plot(n,x2) title("Deconvolved Signal Using ""least-squares"" Method")
自 R2023b 起
创建两个向量。计算与 xin 大小相同的 xin 和 h 的卷积的中心部分。卷积信号 y 的中心部分的长度为 7，而不是全长 length(xin)+length(h)-1（即 10）。
xin = [-1 2 3 -2 0 1 2];
h = [2 4 -1 1];
y = conv(xin,h,"same")y = 1×7
15 5 -9 7 6 7 -1
求出信号 y 关于冲激响应 h 的最小二乘反卷积。使用 "same" 选项指定卷积信号 y 仅为中心部分，其中 y = conv(x,h,"same") + r。显示 deconv 在舍入误差内恢复了 x 中的原始信号。
[x,r] = deconv(y,h,"same",Method="least-squares")
x = 1×7
-1.0000 2.0000 3.0000 -2.0000 0.0000 1.0000 2.0000
r = 1×7
10-14 ×
0 0.0888 0.1776 0 0 0 0
自 R2023b 起
创建两个向量，每个向量包含两个元素，并使用 "valid" 选项求其卷积。此选项仅返回计算的没有补零边缘的卷积部分。在本例中，卷积信号 y 只有一个元素。
xin = [-1 2];
h = [2 5];
y = conv(xin,h,"valid")y = -1
求卷积信号 y 关于冲激响应 h 的最小二乘反卷积。使用 "valid" 选项时，deconv 并不始终返回 x 中的原始信号，而是返回最小化 norm(x) 的反卷积问题的解。
[x,r] = deconv(y,h,"valid",Method="least-squares")
x = 1×2
-0.1724 -0.0690
r = -3.3307e-16
要检查该解，您可以求计算信号 x 与 h 的全卷积。此卷积信号的中心部分与定义反卷积问题的原始 y 相同。
yfull = conv(x,h,"full")yfull = 1×3
-0.3448 -1.0000 -0.3448
在此问题中，deconv 返回与原始信号不同的信号，因为它求解一个具有两个变量的方程，即 。此方程组是欠定方程组，意味着此方程组的变量数目多于方程数目。当使用最小二乘法将残差范数（即 norm(y - conv(x,h,"valid"))）最小化到 0 时，此方程组有无限个解。因此，deconv 也求出一个最小化 norm(x) 的解。
下图说明了此欠定问题的情况。蓝线表示方程 的无限多个解。橙色圆圈表示从原点到解线的最小距离。deconv 返回的解在这条线与圆圈之间的切点上，指示离原点最近的解。
自 R2023b 起
创建两个信号 x 和 h，并求其卷积。对 y 的卷积信号添加一些随机噪声。
N = 200;
n = 0.1*(1:N);
rng("default")
x = 2*exp(-0.8*(n - 8).^2) - 4*exp(-2*(n - 10).^2);
h = 2.*exp(-1*(n - 5).^2).*cos(4*n);
y = conv(x,h);
y = y + max(y)*0.05*randn(1,length(y));绘制原始信号、冲激响应和卷积信号。
figure tiledlayout(3,1) nexttile plot(n,x) title("Original Signal") nexttile plot(n,h) title("Impulse Response") nexttile plot(0.1*(1:length(y)),y) title("Convolved Signal with Added Noise")
接下来，通过使用没有正则化因子的最小二乘法，求含噪信号 y 关于冲激响应 h 的反卷积。默认情况下，正则化因子为 0。
[x1,r1] = deconv(y,h,Method="least-squares");绘制原始信号和反卷积信号。此处，没有正则化因子的 deconv 函数无法从含噪信号中恢复原始信号。
figure; tiledlayout(3,1); nexttile plot(n,x) title("Original Signal") nexttile plot(n,x1) title("Deconvolved Signal Without Regularization");
改为通过使用正则化因子为 1 的最小二乘法，求 y 关于 h 的反卷积。对于病态反卷积问题，例如涉及含噪信号的问题，您可以指定正则化因子以便在最小二乘解中不会出现过拟合。
[x2,r2] = deconv(y,h,Method="least-squares",RegularizationFactor=1);绘制此反卷积信号。此处，具有指定正则化因子的 deconv 函数恢复原始信号。
nexttile
plot(n,x2)
title("Deconvolved Signal Using Regularization")
输入参数
名称-值参数
输出参量
参考
[1] Nagy, James G. “Fast Inverse QR Factorization for Toeplitz Matrices.” SIAM Journal on Scientific Computing 14, no. 5 (September 1993): 1174–93. https://doi.org/10.1137/0914070.
