使用模型预测控制进行 PMSM 的磁场定向控制
此示例采用模型预测控制 (MPC) 技术来控制三相永磁同步电机 (PMSM) 的转速。MPC 是一种控制技术,它通过调整和优化控制系统的输入,以最小化预测系统输出的误差,并在一段时间内实现参考控制目标。该技术涉及求解目标函数,并在每个采样时间点 (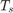 ) 寻找最优输入序列。每个时间步结束后,将当前系统状态视为初始状态,并重复上述过程。
) 寻找最优输入序列。每个时间步结束后,将当前系统状态视为初始状态,并重复上述过程。

优化器基于在特定边界和约束条件下求解目标函数,为模型提供最优输入。在预测阶段,利用动态离散时间模型对被控对象的未来响应进行预测,预测时长可达 Np 个采样间隔,该时长称为预测时限。在优化步骤中,通过求解目标函数以获得最佳控制输入,该过程持续至 Nc 个采样间隔,该区间被称为预测响应的控制时域。控制时限仍小于或等于预测时限。
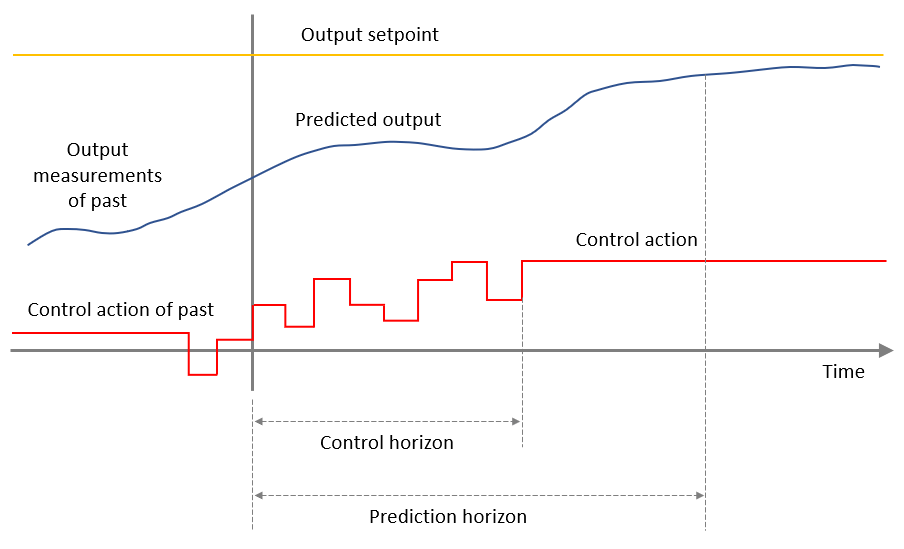
该示例采用 MPC 控制器作为电流控制器(在磁场定向控制或 FOC 算法中),以优化 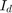 和
和 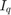 电流,并改变
电流,并改变 d 轴和 q 轴控制器的电压输出,使其在一段时间内满足参考控制目标。
目标函数被推导为以下项的线性和:
[W1 * (error in output)] + [W2 * (rate of change of input)] + [W3 * (error in input)]
其中,W1、W2 和 W3 为权重系数。
该示例使用模型初始化脚本定义以下三个参数的权重系数(或权重)。
1.输入:![$\left[ {{I_d} = 0,{I_q} = 0} \right]$](../../examples/mcb/win64/RunFieldOrientedControlModelPredictiveControlExample_eq17867277116764116776.png)
2.输入变化率:![$\left[ {{I_d} = 0.01,{I_q} = 0.01} \right]$](../../examples/mcb/win64/RunFieldOrientedControlModelPredictiveControlExample_eq13958064958685704276.png)
3.测得的输出:![$\left[ {{V_d} = 1,{V_q} = 1} \right]$](../../examples/mcb/win64/RunFieldOrientedControlModelPredictiveControlExample_eq05190547202861412436.png)
因此,在默认情况下,该示例在计算预测输出误差时,将最大权重赋予输出变量参数(对应于  和
和 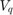 电压)。您可以通过示例中提供的模型初始化脚本,修改用于错误计算的权重值。
电压)。您可以通过示例中提供的模型初始化脚本,修改用于错误计算的权重值。
该示例还控制 MPC 输入(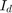 和
和 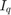 )与 MPC 输出(
)与 MPC 输出( 和
和 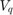 ),其操作范围如下面的下限和上限所示:
),其操作范围如下面的下限和上限所示:
输入


测得的输出

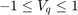
注意:输入的变化率没有上下限。
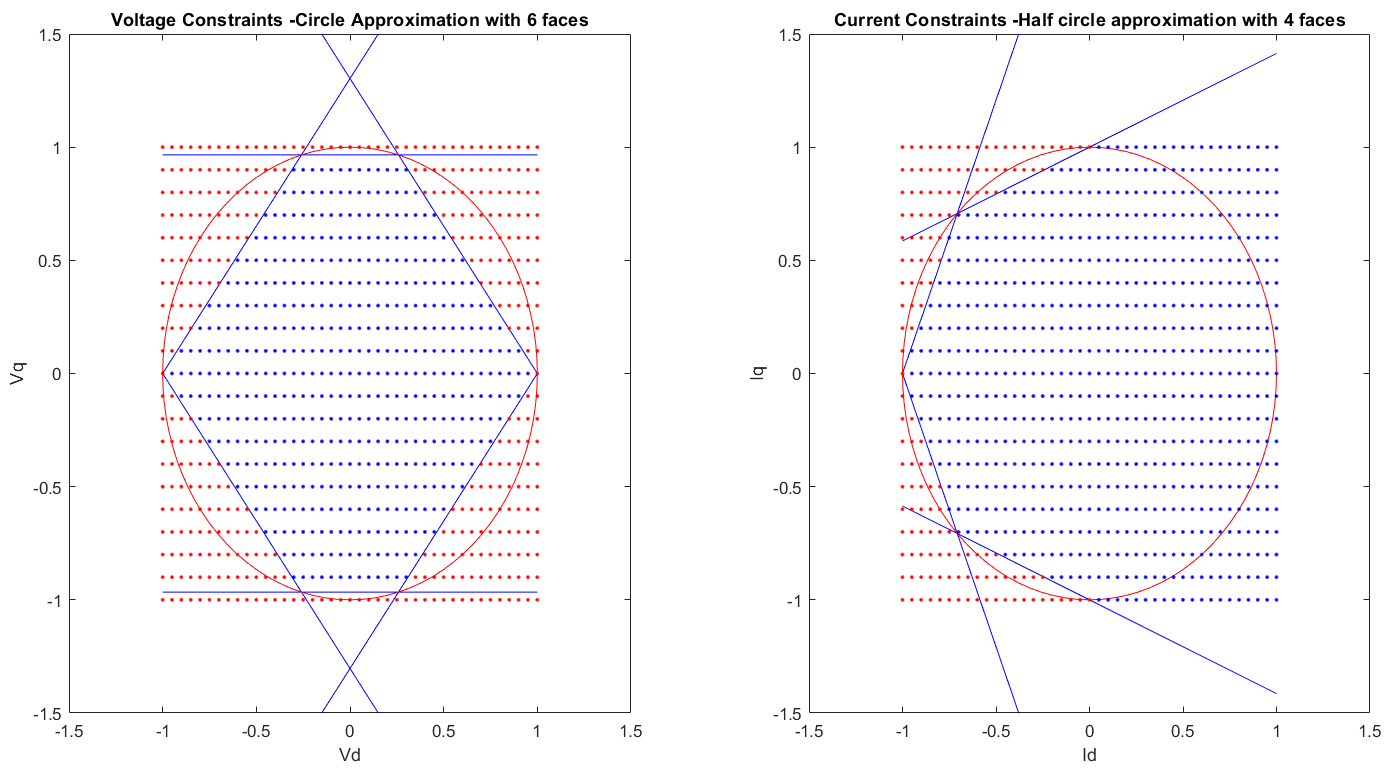
为保持约束的线性,可考虑采用多面体逼近法。通过用六边形逼近可行区域,可在精度与约束数量之间达成可接受的权衡。由于定子电流的直流分量 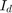 在绝大多数情况下都接近于零(仅在磁通弱化操作期间会呈现负值),因此可将约束
在绝大多数情况下都接近于零(仅在磁通弱化操作期间会呈现负值),因此可将约束 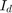 视为小于或等于零,从而减少约束数量。
视为小于或等于零,从而减少约束数量。
下图展示了 MPC 输出电压( 和
和 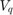 ,采用具有 6 个面的圆形近似)与 MPC 输入电流(
,采用具有 6 个面的圆形近似)与 MPC 输入电流(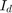 和
和 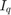 ,采用具有 4 个面的半圆形近似)约束的图形化表示。您可以使用 MATLAB 命令
,采用具有 4 个面的半圆形近似)约束的图形化表示。您可以使用 MATLAB 命令 mcb_getMPCObject(pmsm,PU_System,Ts_current,T_pwm,1) 生成这些图。
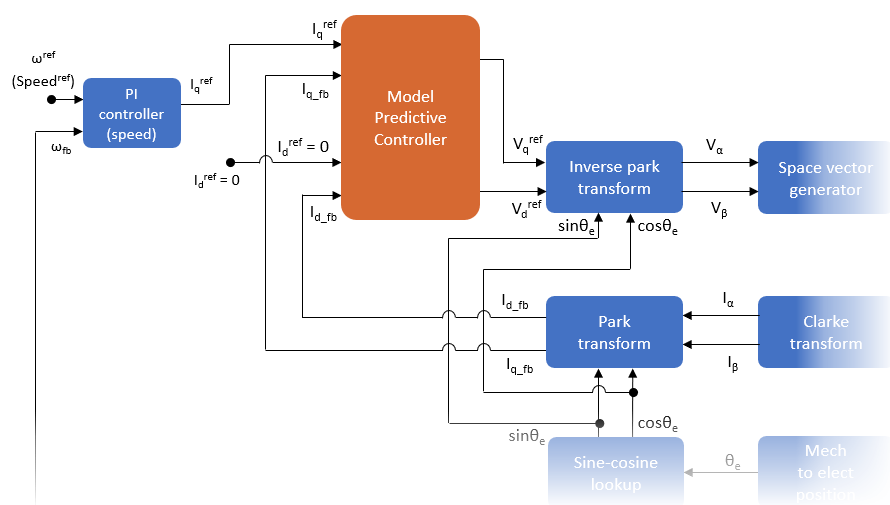
注意:本示例中模型初始化脚本使用的采样时间 (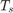 ) 基于对特定硬件的测试结果。您可以为不同类型的硬件更改采样时间,这会反过来影响 MPC 的运行。
) 基于对特定硬件的测试结果。您可以为不同类型的硬件更改采样时间,这会反过来影响 MPC 的运行。
有关 MPC 的详细信息,请参阅What Is Model Predictive Control? (Model Predictive Control Toolbox)。
模型
该示例包含模型 mcb_pmsm_foc_mpc_qep_f28379d
您可以将这些模型用于仿真和代码生成。
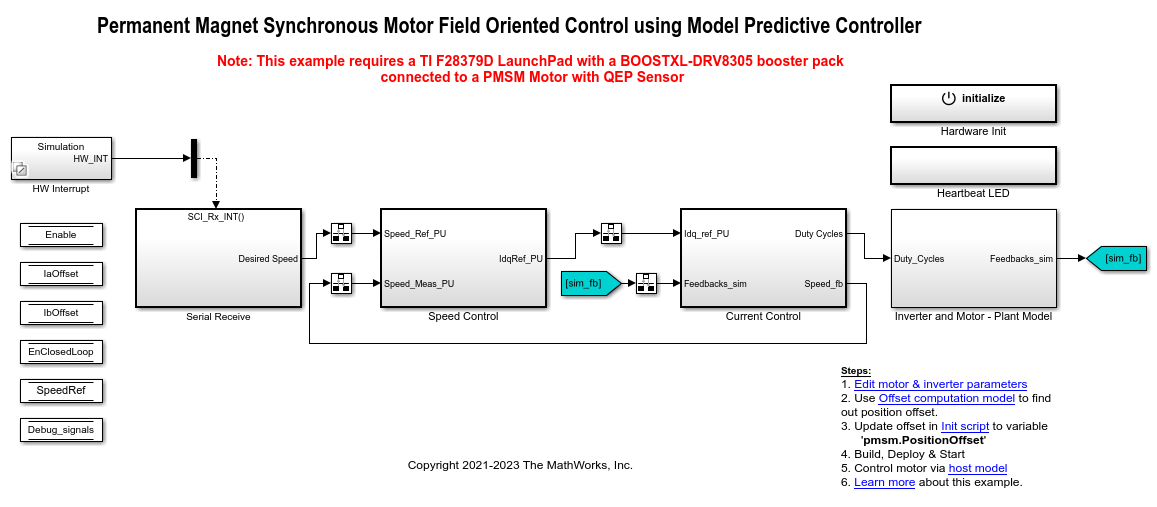
对于可用于不同硬件配置的模型名称,请参阅“生成代码并将模型部署到目标硬件”一节中的“必需的硬件”主题。
必需的 MathWorks 产品
要仿真模型,您需要:
Motor Control Blockset™
Model Predictive Control Toolbox™
要生成代码并部署模型,您需要:
Motor Control Blockset
Model Predictive Control Toolbox
Embedded Coder®
C2000™ Microcontroller Blockset
前提条件
1.获取电机参数。我们对 Simulink® 模型提供了默认电机参数,您可以用电机数据表或其他来源的值替换这些默认值。
不过,如果您有电机控制硬件,则可以通过使用 Motor Control Blockset 参数估计工具来估计要使用的电机的参数。有关说明,请参阅。
参数估计工具使用估计的电机参数更新 motorParam 变量(在 MATLAB® 工作区中)。
2.如果您从数据表或其他来源获得电机参数,请在与 Simulink® 模型相关联的模型初始化脚本中更新电机参数和逆变器参数。有关说明,请参阅估计控制增益和使用工具函数。
如果您使用参数估计工具,则可以在模型初始化脚本中更新逆变器参数,但不能更新电机参数。该脚本会自动从更新后的 motorParam 工作区变量中提取电机参数。
仿真模型
此示例支持仿真。请按照以下步骤仿真模型。
1.打开此示例附带的一个模型。
2.点击仿真选项卡上的运行来仿真该模型。
3.点击仿真选项卡上的数据检查器来查看和分析仿真结果。
生成代码并将模型部署到目标硬件
本节将指导您生成代码并在目标硬件上运行 FOC 算法。
此示例使用一个主机模型和一个目标模型。主机模型是控制器硬件板的一个用户界面。您可以在主机上运行主机模型。使用主机模型的前提条件是将目标模型部署到控制器硬件板上。主机模型使用串行通信对目标 Simulink® 模型发出指令,并以闭环控制方式运行电机。
必需的硬件
此示例支持此硬件配置。您还可以在 MATLAB® 命令提示符下使用目标模型名称打开对应硬件配置的模型。
LAUNCHXL-F28379D 控制器 + BOOSTXL-DRV8305 逆变器:mcb_pmsm_foc_mpc_qep_f28379d
有关与前述硬件配置相关的连接,请参阅 LAUNCHXL-F28069M 和 LAUNCHXL-F28379D 配置。
生成代码并在目标硬件上运行模型
1.仿真目标模型并观测仿真结果。
2.完成硬件连接。
3.该模型自动计算 ADC(或电流)偏移值。要禁用此功能(默认启用),请在模型初始化脚本中将变量 inverter.ADCOffsetCalibEnable 的值更新为 0。
您也可以计算 ADC 偏移值,并在模型初始化脚本中手动更新它。有关说明,请参阅以开环控制方式运行三相 AC 电机并校准 ADC 偏移量。
4.计算正交编码器索引偏移值,并在与目标模型相关联的模型初始化脚本中更新它。有关说明,请参阅 PMSM 的正交编码器偏移量校准。
注意:验证连接到电机的正交编码器中可用的刻线数量。检查并更新模型初始化脚本中可用的变量 pmsm.QEPSlits。此变量对应于正交编码器模块的 Encoder slits 参数。有关 Encoder slits 和 Encoder counts per slit 参数的更多详细信息,请参阅Quadrature Decoder。
5.按所需的硬件配置打开目标模型。如果您要更改该模型的默认硬件配置设置,请参阅模型配置参数。
6.将一个示例程序加载到 LAUNCHXL-F28379D 的 CPU2(例如使用 GPIO31 操作 CPU2 蓝色 LED 的程序 c28379D_cpu2_blink.slx),以确保 CPU2 没有错误地配置为使用预留给 CPU1 的板载外设。有关示例程序或模型的详细信息,请参阅 Getting Started with Texas Instruments C2000 Microcontroller Blockset (C2000 Microcontroller Blockset) 中的“任务 2 - 为 TI Delfino F28379D LaunchPad(双核)创建、配置和运行模型”部分。
7.点击硬件选项卡上的编译、部署和启动以将目标模型部署到硬件上。
8.点击目标模型中的主机模型超链接以打开关联的主机模型。

有关主机模型和目标模型之间串行通信的详细信息,请参阅Host-Target Communication。
9.在与目标模型关联的模型初始化脚本中,使用变量 target.comport 指定通信端口。该示例使用此变量来更新主机模型中可用的 Host Serial Setup、Host Serial Receive 和 Host Serial Transmit 模块的端口参数。
10.更新主机模型中的 Reference Speed 值。
11.点击仿真选项卡上的运行以运行主机模型。
12.将 Start / Stop Motor 开关的位置切换到 On 以开始运行电机。
13.使用调试信号部分选择您要监控的调试信号。在主机模型的 Time Scope 中,观测来自 RX 子系统的调试信号。
参考资料
G. Cimini, D. Bernardini, A. Bemporad and S. Levijoki, "Online model predictive torque control for Permanent Magnet Synchronous Motors," 2015 IEEE International Conference on Industrial Technology (ICIT), 2015, pp. 2308-2313, doi:10.1109/ICIT.2015.7125438.
S. Chai, L. Wang and E. Rogers, "Cascade model predictive control of a PMSM with periodic disturbance rejection," 2011 Australian Control Conference, 2011, pp. 309-314.