plan
Description
Examples
Input Arguments
Output Arguments
Algorithms
The plan function implements the MPNet path planning algorithm
presented in [1]. This section gives a brief
overview of the algorithm.
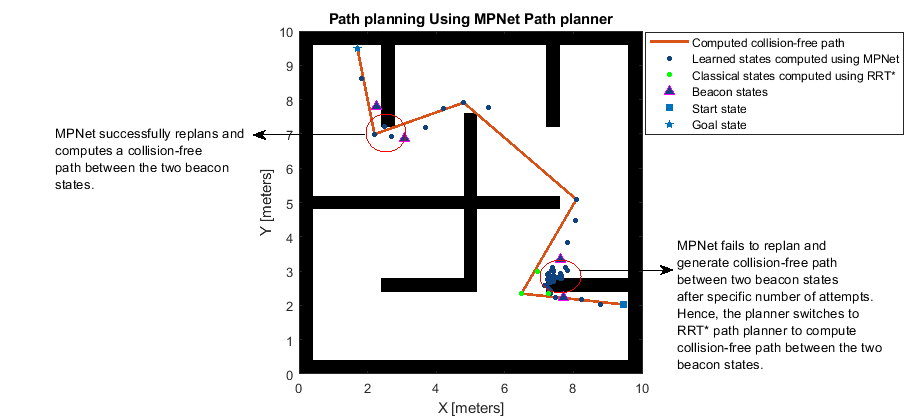
The MPNet path planner computes a coarse path consisting of learned states that lie along the global path between start and goal states. If the path connecting any learned states is not collision-free, the MPNet path planner performs replanning only for that segment in the coarse path.
Two consecutive learned states that are in the free space and cannot be connected without colliding with an obstacle are termed beacon states. The MPNet path planner selects these beacon states as new start and goal points and attempts to find a collision-free path to connect them. This step is referred to as replanning. The path planner makes a limited number of attempts to find this path. If it is not able to find the path within a specified number of attempts, it switches to using a classical path planner. The MPNet path planner determines the maximum number of attempts it can make before switching to a classical planner by using the
MaxNumLearnedStatesproperty.At every planning and replanning step, the planner applies the lazy states contraction (LSC) approach to remove redundant states computed by the planner. This results in reduced computational complexity and helps the planner find the shortest collision-free path between the actual start and goal states.
References
[1] Qureshi, Ahmed Hussain, Yinglong Miao, Anthony Simeonov, and Michael C. Yip. “Motion Planning Networks: Bridging the Gap Between Learning-Based and Classical Motion Planners.” IEEE Transactions on Robotics 37, no. 1 (February 2021): 48–66. https://doi.org/10.1109/TRO.2020.3006716.
Extended Capabilities
Version History
Introduced in R2024a
![Figure contains an axes object. The axes object with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 3 objects of type image, line. One or more of the lines displays its values using only markers These objects represent Start, Goal.](../../examples/nav/win64/PlanPathBetweenTwoStatesUsingMPNetPathPlannerExample_01.png)
![Figure contains an axes object. The axes object with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 4 objects of type image, line. One or more of the lines displays its values using only markers These objects represent Planned path, Start state, Goal state.](../../examples/nav/win64/PlanPathBetweenTwoStatesUsingMPNetPathPlannerExample_02.png)
![Figure contains an axes object. The axes object with title Binary Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 7 objects of type image, line. One or more of the lines displays its values using only markers These objects represent Planned path, Learned states, Classical states, Beacon states, Start state, Goal state.](../../examples/nav/win64/PlanPathBetweenTwoStatesUsingMPNetPathPlannerExample_03.png)
![Figure contains an axes object. The axes object with title Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 4 objects of type image, line. One or more of the lines displays its values using only markers These objects represent Planned path, Start state, Goal state.](../../examples/nav/win64/PlanPathInDubinsStateSpaceUsingMPNetPathPlannerExample_01.png)
![Figure contains an axes object. The axes object with title Occupancy Grid, xlabel X [meters], ylabel Y [meters] contains 6 objects of type image, line. One or more of the lines displays its values using only markers These objects represent Planned path, Learned states, Beacon states, Start state, Goal state.](../../examples/nav/win64/PlanPathInDubinsStateSpaceUsingMPNetPathPlannerExample_02.png)