Main Content

使用 fgoalattain 进行信号处理

考虑设计一个线性相位有限脉冲响应 (FIR) 滤波器。问题是设计一个低通滤波器，其在 0 到 0.1 Hz 之间的所有频率上幅度为 1，在 0.15 到 0.5 Hz 之间的幅度为 0。

这种滤波器的频率响应 H(f) 定义为

H(f)=∑n=02Mh(n)e−j2πfn=A(f)e−j2πfM,A(f)=∑n=0M−1a(n)cos(2πfn),(1)

其中 A(f) 是频率响应的幅度。一个解是将目标实现方法应用于频率响应的幅度。给定一个计算幅度的函数，fgoalattain 将尝试改变幅度系数 a(n) 直到幅度响应在一定容差范围内与所需响应匹配。计算幅度响应的函数在 filtmin.m 中给出。该函数使用幅度函数系数 a 和感兴趣的频域离散化 w。

要设置目标实现问题，您必须为问题指定 goal 和 weights。对于 0 到 0.1 之间的频率，目标是 1。对于 0.15 到 0.5 之间的频率，目标是零。未指定 0.1 到 0.15 之间的频率，因此此范围内不需要目标或权重。

该信息存储在传递给 fgoalattain 的变量 goal 中。goal 的长度与函数 filtmin 返回的长度相同。为了使目标得到同等满足，通常将 weight 设置为 abs(goal)。但是，由于某些目标为零，使用 weight=abs(goal) 的效果将迫使 weight 为 0 的目标作为硬约束得到满足，而 weight 为 1 的目标可能达不到要求（请参阅 目标达成方法）。因为所有目标的量级都很接近，所以对所有目标使用统一的 weight 将赋予它们同等的优先级。（当 goal 的幅度差异较大时，使用 abs(goal) 作为权重更为重要。）另外，设置 

options = optimoptions('fgoalattain','EqualityGoalCount',length(goal));

指定每个目标应尽可能接近其目标值（既不大于也不小于）。

步骤 1：写入文件 filtmin.m

function y = filtmin(a,w)
n = length(a);
y = cos(w'*(0:n-1)*2*pi)*a ;

步骤 2：调用优化例程

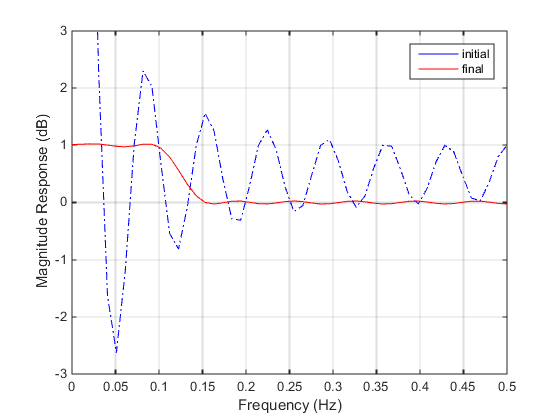
% Plot with initial coefficients
a0 = ones(15,1);
incr = 50;
w = linspace(0,0.5,incr);

y0 = filtmin(a0,w);
clf, plot(w,y0,'-.b');
drawnow;

% Set up the goal attainment problem
w1 = linspace(0,0.1,incr) ;
w2 = linspace(0.15,0.5,incr);
w0 = [w1 w2];
goal = [1.0*ones(1,length(w1)) zeros(1,length(w2))];
weight = ones(size(goal)); 

% Call fgoalattain
options = optimoptions('fgoalattain','EqualityGoalCount',length(goal));
[a,fval,attainfactor,exitflag]=fgoalattain(@(x)filtmin(x,w0),...
    a0,goal,weight,[],[],[],[],[],[],[],options);

% Plot with the optimized (final) coefficients
y = filtmin(a,w);
hold on, plot(w,y,'r')
axis([0 0.5 -3 3])
xlabel('Frequency (Hz)')
ylabel('Magnitude Response (dB)')
legend('initial', 'final')
grid on

将计算出的幅度响应与初始系数和最终系数 (具有初始和最终震级系数的震级响应) 进行比较。请注意，您可以使用 Signal Processing Toolbox™ 软件中的 firpm (Signal Processing Toolbox) 函数来设计此过滤器。

具有初始和最终震级系数的震级响应

The initial response looks like a damped sinusoid as the frequency (x-axis) increases. The final response is close to a piecewise linear function with value 1 at frequencies 0 to 0.1, linear from 1 to 0 as frequency increases from 0.1 to 0.15, and remains near zero for frequencies above 0.15.

另请参阅

相关主题