Dimensions of Solutions, Gradients, and Fluxes

solvepde returns a StationaryResults or TimeDependentResults object whose properties contain the solution and its gradient at the mesh nodes. You can interpolate the solution and its gradient to other points in the geometry by using interpolateSolution and evaluateGradient. You also can compute flux of the solution at the mesh nodes and at arbitrary points by using evaluateCGradient.

Note

solvepde does not compute components of flux of a PDE solution. To compute flux of the solution at the mesh nodes, use evaluateCGradient.

solvepdeeig returns an EigenResults object whose properties contain the solution eigenvectors calculated at the mesh nodes. You can interpolate the solution to other points by using interpolateSolution.

The dimensions of the solution, its gradient, and flux of the solution depend on:

The number of geometric evaluation points.
- For results returned by solvepde or solvepdeeig, this is the number of mesh nodes.
- For results returned by interpolateSolution,evaluateGradient, and evaluateCGradient this is the number of query points.
The number of equations.
- For results returned by solvepde or solvepdeeig, this is the number of equations in the system.
- For results returned by interpolateSolution,evaluateGradient, and evaluateCGradient, this is the number of query equation indices.
The number of times for a time-dependent problem or number of modes for an eigenvalue problem.
- For results returned by solvepde, this is the number of solution times (specified as an input to solvepde).
- For results returned by solvepdeeig, this is the number of eigenvalues.
- For results returned by interpolateSolution, evaluateGradient, and evaluateCGradient, this is the number of query times for time-dependent problems or query modes for eigenvalue problems.

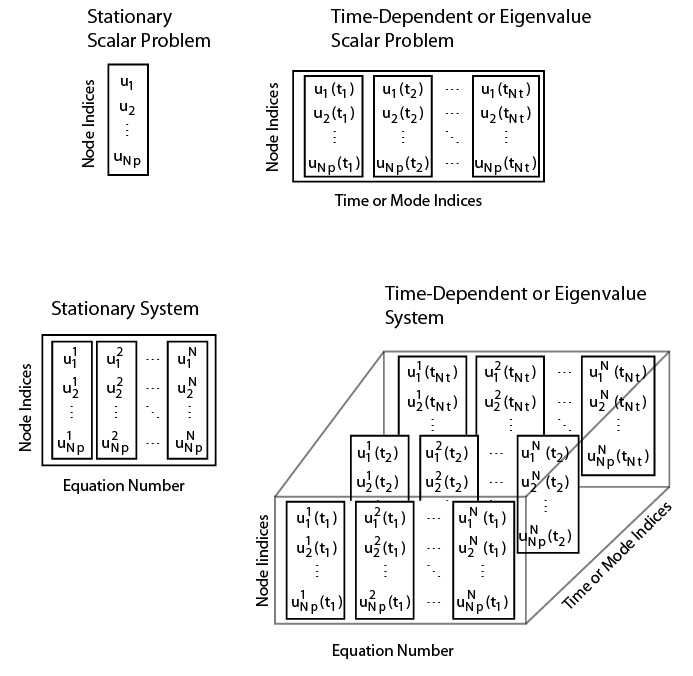
Dimensions for stationary, time-dependent, and eigenvalue scalar problems and systems

Suppose you have a problem in which:

Np is the number of nodes in the mesh.
Nt is the number of times for a time-dependent problem or number of modes for an eigenvalue problem.
N is the number of equations in the system.

Suppose you also compute the solution, its gradient, or flux of the solution at other points ("query points") in the geometry by using interpolateSolution, evaluateGradient, or evaluateCGradient, respectively. Here:

Nqp is the number of query points.
Nqt is the number of query times for a time-dependent problem or number of query modes for an eigenvalue problem.
Nq is the number of query equations indices.

The tables show how to index into the solution returned by solvepde or solvepdeeig, where:

iP contains the indices of nodes.
iT contains the indices of times for a time-dependent problem or mode numbers for an eigenvalue problem.
iN contains the indices of equations.

The tables also show the dimensions of solutions, gradients, and flux of the solution at nodal locations (returned by solvepde,solvepdeeig, and evaluateCGradient) and the dimensions of interpolated solutions and gradients (returned by interpolateSolution, evaluateGradient, and evaluateCGradient).

Stationary PDE problem Access solution and components of gradient Size of NodalSolution, XGradients, YGradients, ZGradients, and components of flux at nodal points Size of solution, components of gradient, and components of flux at query points

Scalar

Stationary PDE problem	Access solution and components of gradient	Size of `NodalSolution`, `XGradients`, `YGradients`, `ZGradients`, and components of flux at nodal points	Size of solution, components of gradient, and components of flux at query points
Scalar	`result.NodalSolution(iP)` `result.XGradients(iP)` `result.YGradients(iP)` `result.ZGradients(iP)`	`Np`-by-1	`Nqp`-by-1
System, `N` > `1`	`result.NodalSolution(iP,iN)` `result.XGradients(iP,iN)` `result.YGradients(iP,iN)` `result.ZGradients(iP,iN)`	`Np`-by-`N`	`Nqp`-by-`N`

result.NodalSolution(iP)

result.XGradients(iP)

result.YGradients(iP)

result.ZGradients(iP)

Np-by-1

Nqp-by-1

System, N > 1

result.NodalSolution(iP,iN)

result.XGradients(iP,iN)

result.YGradients(iP,iN)

result.ZGradients(iP,iN)

Np-by-N

Nqp-by-N

Time-dependent PDE problem Access solution and components of gradient Size of NodalSolution, XGradients, YGradients, ZGradients, and components of flux at nodal points Size of solution, components of gradient, and components of flux at query points

Scalar

Time-dependent PDE problem	Access solution and components of gradient	Size of `NodalSolution`, `XGradients`, `YGradients`, `ZGradients`, and components of flux at nodal points	Size of solution, components of gradient, and components of flux at query points
Scalar	`result.NodalSolution(iP,iT)` `result.XGradients(iP,iT)` `result.YGradients(iP,iT)` `result.ZGradients(iP,iT)`	`Np`-by-`Nt`	`Nqp`-by-`Nqt`
System, `N` > `1`	`result.NodalSolution(iP,iN,iT)` `result.XGradients(iP,iN,iT)` `result.YGradients(iP,iN,iT)` `result.ZGradients(iP,iN,iT)`	`Np`-by-`N`-by-`Nt`	`Nqp`-by-`Nq`-by-`Nqt`

result.NodalSolution(iP,iT)

result.XGradients(iP,iT)

result.YGradients(iP,iT)

result.ZGradients(iP,iT)

Np-by-Nt

Nqp-by-Nqt

System, N > 1

result.NodalSolution(iP,iN,iT)

result.XGradients(iP,iN,iT)

result.YGradients(iP,iN,iT)

result.ZGradients(iP,iN,iT)

Np-by-N-by-Nt

Nqp-by-Nq-by-Nqt

PDE eigenvalue problem	Access eigenvectors	Size of `Eigenvectors`	Size of interpolated eigenvectors
Scalar	`result.Eigenvectors(iP,iT)`	`Np`-by-`Nt`	`Nqp`-by-`Nqt`
System, `N` > `1`	`result.Eigenvectors(iP,iN,iT)`	`Np`-by-`N`-by-`Nt`	`Nqp`-by-`Nq`-by-`Nqt`

Dimensions of Solutions, Gradients, and Fluxes

See Also