pdeeig

(Not recommended) Solve eigenvalue PDE problem

pdeeig is not recommended. Use solvepdeeig instead.

Syntax

[v,l] =
pdeeig(model,c,a,d,r)

[v,l] =
pdeeig(b,p,e,t,c,a,d,r)

[v,l] =
pdeeig(Kc,B,M,r)

Description

[v,l] = pdeeig(model,c,a,d,r) produces the solution to the FEM formulation of the scalar PDE eigenvalue problem

$- \nabla \cdot (c \nabla u) + a u = λ d u on Ω$

or the system PDE eigenvalue problem

$- \nabla \cdot (c \otimes \nabla u) + a u = λ d u on Ω$

with geometry, boundary conditions, and mesh specified in model, a PDEModel object.

The eigenvalue PDE problem is a homogeneous problem, i.e., only boundary conditions where g = 0 and r = 0 can be used. The nonhomogeneous part is removed automatically.

example

[v,l] = pdeeig(b,p,e,t,c,a,d,r) solves for boundary conditions described in b, and the finite element mesh in [p,e,t].

example

[v,l] = pdeeig(Kc,B,M,r) produces the solution to the generalized sparse matrix eigenvalue problem

Kc u_i = λB´MBu_i
u = Bu_i

with Real(λ) in the interval r.

example

Examples

collapse all

Eigenvalues and Eigenvectors of L-Shaped Membrane

Open Live Script

Compute the eigenvalues that are less than 100, and compute the corresponding eigenmodes for $- \nabla u = λ u$ on the geometry of the L-shaped membrane.

model = createpde;
geometryFromEdges(model,@lshapeg);
applyBoundaryCondition(model,'edge',1:model.Geometry.NumEdges,'u',0);
generateMesh(model,'GeometricOrder','linear','Hmax',0.02);
c = 1;
a = 0;
d = 1;
r = [-Inf 100];
[v,l] = pdeeig(model,c,a,d,r);
l(1)                    % first eigenvalue

ans = 
19.7491

Display the first eigenmode, and compare it to the built-in membrane plot.

pdeplot(model,'XYData',v(:,1),'ZData',v(:,1))

Figure contains an axes object. The axes object contains an object of type patch.

figure 
membrane(1,20,9,9)      % the MATLAB function

Figure contains an axes object. The axes object contains an object of type surface.

Compute the sixteenth eigenvalue, and plot the sixteenth eigenmode.

l(16)                   % sixteenth eigenvalue

ans = 
98.9431

figure
pdeplot(model,'XYData',v(:,16),'ZData',v(:,16))    % sixteenth eigenmode

Figure contains an axes object. The axes object contains an object of type patch.

Eigenvalues and Eigenvectors of the L-Shaped Membrane Using Legacy Syntax

Open Live Script

Compute the eigenvalues that are less than 100, and compute the corresponding eigenmodes for $- \nabla u = λ u$ on the geometry of the L-shaped membrane, using the legacy syntax.

Use the geometry in lshapeg. For more information about this syntax, see Parameterized Function for 2-D Geometry Creation.

g = @lshapeg;
pdegplot(g,'EdgeLabels','on')
axis equal
ylim([-1.1,1.1])

Figure contains an axes object. The axes object contains 11 objects of type line, text.

Set zero Dirichlet boundary conditions using the lshapeb function.

b = @lshapeb;

Set coefficients c = 1, a = 0, and d = 1. Collect eigenvalues up to 100.

c = 1;
a = 0;
d = 1;
r = [-Inf 100];

Generate a mesh and solve the eigenvalue problem.

[p,e,t] = initmesh(g,'Hmax',0.02);
[v,l] = pdeeig(b,p,e,t,c,a,d,r);

Find the first eigenvalue.

l(1)

ans = 
9.6481

Eigenvalues and Eigenvectors Using Finite Element Matrices

Open Live Script

Import a simple 3-D geometry and find eigenvalues and eigenvectors from the associated finite element matrices.

Create a model and import the BracketWithHole.stl geometry.

model = createpde();
importGeometry(model,'BracketWithHole.stl');
figure
pdegplot(model,'FaceLabels','on')
view(30,30)
title('Bracket with Face Labels')

Figure contains an axes object. The axes object with title Bracket with Face Labels contains 6 objects of type quiver, text, patch, line.

figure
pdegplot(model,'FaceLabels','on')
view(-134,-32)
title('Bracket with Face Labels, Rear View')

Figure contains an axes object. The axes object with title Bracket with Face Labels, Rear View contains 6 objects of type quiver, text, patch, line.

Set coefficients c = 1, a = 0, and d = 1. Collect eigenvalues that are less than 100.

c = 1;
a = 0;
d = 1;
r = [-Inf 100];

Generate a mesh for the model.

generateMesh(model);

Create the associated finite element matrices.

[Kc,~,B,~] = assempde(model,c,a,0);
[~,M,~] = assema(model,0,d,0);

Solve the eigenvalue problem.

[v,l] = pdeeig(Kc,B,M,r);

Look at the first two eigenvalues.

l([1,2])

ans = 2×1

   -0.0000
   42.8014

Plot the solution corresponding to eigenvalue 2.

pdeplot3D(model,'ColorMapData',v(:,2))

Figure contains an axes object. The hidden axes object contains 5 objects of type patch, quiver, text.

Input Arguments

collapse all

`model` — PDE model
`PDEModel` object

PDE model, specified as a PDEModel object.

Example: model = createpde

`c` — PDE coefficient
scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

PDE coefficient, specified as a scalar, matrix, character vector, character array, string scalar, string vector, or coefficient function. c represents the c coefficient in the scalar PDE

$- \nabla \cdot (c \nabla u) + a u = λ d u on Ω$

or the system PDE eigenvalue problem

$- \nabla \cdot (c \otimes \nabla u) + a u = λ d u on Ω$

Example: 'cosh(x+y.^2)'

Data Types: double | char | string | function_handle
Complex Number Support: Yes

`a` — PDE coefficient
scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

PDE coefficient, specified as a scalar, matrix, character vector, character array, string scalar, string vector, or coefficient function. a represents the a coefficient in the scalar PDE

$- \nabla \cdot (c \nabla u) + a u = λ d u on Ω$

or the system PDE eigenvalue problem

$- \nabla \cdot (c \otimes \nabla u) + a u = λ d u on Ω$

Example: 2*eye(3)

Data Types: double | char | string | function_handle
Complex Number Support: Yes

`d` — PDE coefficient
scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

PDE coefficient, specified as a scalar, matrix, character vector, character array, string scalar, string vector, or coefficient function. d represents the d coefficient in the scalar PDE

$- \nabla \cdot (c \nabla u) + a u = λ d u on Ω$

or the system PDE eigenvalue problem

$- \nabla \cdot (c \otimes \nabla u) + a u = λ d u on Ω$

Example: 2*eye(3)

Data Types: double | char | string | function_handle
Complex Number Support: Yes

`r` — Eigenvalue range
two-element real vector

Eigenvalue range, specified as a two-element real vector. Real parts of eigenvalues λ fall in the range r(1) ≤ λ ≤ r(2). r(1) can be -Inf. The algorithm returns all eigenvalues in this interval in the l output, up to a maximum of 99 eigenvalues.

Example: [-Inf,100]

Data Types: double

`b` — Boundary conditions
boundary matrix | boundary file

Boundary conditions, specified as a boundary matrix or boundary file. Pass a boundary file as a function handle or as a file name. A boundary matrix is generally an export from the PDE Modeler app.

Example: b = 'circleb1', b = "circleb1", or b = @circleb1

Data Types: double | char | string | function_handle

`p` — Mesh points
matrix

Mesh points, specified as a 2-by-Np matrix of points, where Np is the number of points in the mesh. For a description of the (p,e,t) matrices, see Mesh Data as [p,e,t] Triples.

Typically, you use the p, e, and t data exported from the PDE Modeler app, or generated by initmesh or refinemesh.

Example: [p,e,t] = initmesh(gd)

Data Types: double

`e` — Mesh edges
matrix

Mesh edges, specified as a 7-by-Ne matrix of edges, where Ne is the number of edges in the mesh. For a description of the (p,e,t) matrices, see Mesh Data as [p,e,t] Triples.

Typically, you use the p, e, and t data exported from the PDE Modeler app, or generated by initmesh or refinemesh.

Example: [p,e,t] = initmesh(gd)

Data Types: double

`t` — Mesh triangles
matrix

Mesh triangles, specified as a 4-by-Nt matrix of triangles, where Nt is the number of triangles in the mesh. For a description of the (p,e,t) matrices, see Mesh Data as [p,e,t] Triples.

Typically, you use the p, e, and t data exported from the PDE Modeler app, or generated by initmesh or refinemesh.

Example: [p,e,t] = initmesh(gd)

Data Types: double

`Kc` — Stiffness matrix
sparse matrix | full matrix

Stiffness matrix, specified as a sparse matrix or as a full matrix. See Elliptic Equations. Typically, Kc is the output of assempde.

`B` — Dirichlet nullspace
sparse matrix

Dirichlet nullspace, returned as a sparse matrix. See Algorithms. Typically, B is the output of assempde.

`M` — Mass matrix
sparse matrix | full matrix

Mass matrix. specified as a sparse matrix or a full matrix. See Elliptic Equations.

To obtain the input matrices for pdeeig, hyperbolic or parabolic, run both assema and assempde:

[Kc,Fc,B,ud] = assempde(model,c,a,f);
[~,M,~] = assema(model,0,d,f);

Note

Create the M matrix using assema with d, not a, as the argument before f.

Data Types: double
Complex Number Support: Yes

Output Arguments

collapse all

`v` — Eigenvectors
matrix

Eigenvectors, returned as a matrix. Suppose

Np is the number of mesh nodes
N is the number of equations
ev is the number of eigenvalues returned in l

Then v has size Np*N-by-ev. Each column of v corresponds to the eigenvectors of one eigenvalue. In each column, the first Np elements correspond to the eigenvector of equation 1 evaluated at the mesh nodes, the next Np elements correspond to equation 2, etc.

Note

Eigenvectors are determined only up to multiple by a scalar, including a negative scalar.

`l` — Eigenvalues
vector

Eigenvalues, returned as a vector. The real parts of l are in the interval r. The real parts of l are monotone increasing.

Limitations

In the standard case c and d are positive in the entire region. All eigenvalues are positive, and 0 is a good choice for a lower bound of the interval. The cases where either c or d is zero are discussed next.

If d = 0 in a subregion, the mass matrix M becomes singular. This does not cause any trouble, provided that c > 0 everywhere. The pencil (K,M) has a set of infinite eigenvalues.
If c = 0 in a subregion, the stiffness matrix K becomes singular, and the pencil (K,M) has many zero eigenvalues. With an interval containing zero, pdeeig goes on for a very long time to find all the zero eigenvalues. Choose a positive lower bound away from zero but below the smallest nonzero eigenvalue.
If there is a region where both c = 0 and d = 0, we get a singular pencil. The whole eigenvalue problem is undetermined, and any value is equally plausible as an eigenvalue.

Some of the awkward cases are detected by pdeeig. If the shifted matrix is singular, another shift is attempted. If the matrix with the new shift is still singular a good guess is that the entire pencil (K,M) is singular.

If you try any problem not belonging to the standard case, you must use your knowledge of the original physical problem to interpret the results from the computation.

Tips

The equation coefficients cannot depend on the solution u or its gradient.

Algorithms

collapse all

Eigenvalue Equations

Partial Differential Equation Toolbox™ software handles the following basic eigenvalue problem:

$- \nabla \cdot (c \nabla u) + a u = λ d u$

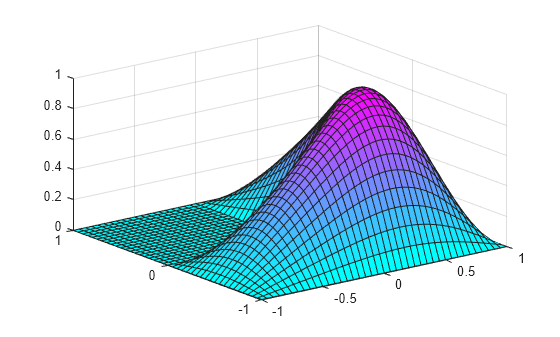
where λ is an unknown complex number. In solid mechanics, this is a problem associated with wave phenomena describing, e.g., the natural modes of a vibrating membrane. In quantum mechanics λ is the energy level of a bound state in the potential well a(x), where x represents a 2-D or 3-D point.

The numerical solution is found by discretizing the equation and solving the resulting algebraic eigenvalue problem. Let us first consider the discretization. Expand u in the FEM basis, multiply with a basis element, and integrate on the domain Ω. This yields the generalized eigenvalue equation

KU = λMU

where the mass matrix corresponds to the right side, i.e.,

$M_{i, j} = \int_{Ω} d (x) ϕ_{j} (x) ϕ_{i} (x) d x$

The matrices K and M are produced by calling assema for the equations

–∇ · (c∇u) + au = 0 and –∇ · (0∇u) + du = 0

In the most common case, when the function d(x) is positive, the mass matrix M is positive definite symmetric. Likewise, when c(x) is positive and we have Dirichlet boundary conditions, the stiffness matrix K is also positive definite.

The generalized eigenvalue problem, KU = λMU, is now solved by the Arnoldi algorithm applied to a shifted and inverted matrix with restarts until all eigenvalues in the user-specified interval have been found.

Let us describe how this is done in more detail. You may want to look at the examples Eigenvalues and Eigenmodes of L-Shaped Membrane or Eigenvalues and Eigenmodes of Square, where actual runs are reported.

First a shift µ is determined close to where we want to find the eigenvalues. When both K and M are positive definite, it is natural to take µ = 0, and get the smallest eigenvalues; in other cases take any point in the interval [lb,ub] where eigenvalues are sought. Subtract µM from the eigenvalue equation and get (K - µM)U = (λ - µ)MU. Then multiply with the inverse of this shifted matrix and get

$\frac{1}{λ - μ} U = {(K - μ M)}^{- 1} M U$

This is a standard eigenvalue problem AU = θU, with the matrix A = (K – µM)^-1M and eigenvalues

$θ_{i} = \frac{1}{λ_{i} - μ}$

where i = 1, . . ., n. The largest eigenvalues θ_i of the transformed matrix A now correspond to the eigenvalues λ_i = µ + 1/θ_i of the original pencil (K,M) closest to the shift µ.

The Arnoldi algorithm computes an orthonormal basis V where the shifted and inverted operator A is represented by a Hessenberg matrix H,

AV_j = V_jH_j,j + E_j.

(The subscripts mean that V_j and E_j have j columns and H_j,j has j rows and columns. When no subscripts are used we deal with vectors and matrices of size n.)

Some of the eigenvalues of this Hessenberg matrix H_j,j eventually give good approximations to the eigenvalues of the original pencil (K,M) when the basis grows in dimension j, and less and less of the eigenvector is hidden in the residual matrix E_j.

The basis V is built one column v_j at a time. The first vector v₁ is chosen at random, as n normally distributed random numbers. In step j, the first j vectors are already computed and form the n ×j matrix V_j. The next vector v_j+1 is computed by first letting A operate on the newest vector v_j, and then making the result orthogonal to all the previous vectors.

This is formulated as $h_{j + 1} v_{j + 1} = A v_{j} - V_{j} h_{j}$ , where the column vector h_j consists of the Gram-Schmidt coefficients, and h_j+1,j is the normalization factor that gives v_j+1 unit length. Put the corresponding relations from previous steps in front of this and get

$A V_{j} = V_{j} H_{j, j} + v_{j + 1} h_{j + 1, j} e_{j}^{T}$

where H_j,j is a j×j Hessenberg matrix with the vectors h_j as columns. The second term on the right-hand side has nonzeros only in the last column; the earlier normalization factors show up in the subdiagonal of H_j,j.

The eigensolution of the small Hessenberg matrix H gives approximations to some of the eigenvalues and eigenvectors of the large matrix operator A_j,j in the following way. Compute eigenvalues θ_i and eigenvectors s_i of H_j,j,

$H_{j, j} s_{i} = s_{i} θ_{i}, i = 1, ..., j$

Then y_i = V_js_i is an approximate eigenvector of A, and its residual is

$r_{i} = A y_{i} - y_{i} θ_{i} = A V_{j} s_{i} - V_{j} s_{i} θ_{i} = (A V_{j} - V_{j} H_{j, j}) s_{i} = v_{j + 1} h_{j + 1, j} s_{i, j}$

This residual has to be small in norm for θ_i to be a good eigenvalue approximation. The norm of the residual is

$‖ r_{i} ‖ = | h_{j + 1, j} s_{j, i} |$

the product of the last subdiagonal element of the Hessenberg matrix and the last element of its eigenvector. It seldom happens that h_j+1,j gets particularly small, but after sufficiently many steps j there are always some eigenvectors s_i with small last elements. The long vector V_j+1 is of unit norm.

It is not necessary to actually compute the eigenvector approximation y_i to get the norm of the residual; we only need to examine the short vectors s_i, and flag those with tiny last components as converged. In a typical case n may be 2000, while j seldom exceeds 50, so all computations that involve only matrices and vectors of size j are much cheaper than those involving vectors of length n.

This eigenvalue computation and test for convergence is done every few steps j, until all approximations to eigenvalues inside the interval [lb,ub] are flagged as converged. When n is much larger than j, this is done very often, for smaller n more seldom. When all eigenvalues inside the interval have converged, or when j has reached a prescribed maximum, the converged eigenvectors, or more appropriately Schur vectors, are computed and put in the front of the basis V.

After this, the Arnoldi algorithm is restarted with a random vector, if all approximations inside the interval are flagged as converged, or else with the best unconverged approximate eigenvector y_i. In each step j of this second Arnoldi run, the vector is made orthogonal to all vectors in V including the converged Schur vectors from the previous runs. This way, the algorithm is applied to a projected matrix, and picks up a second copy of any double eigenvalue there may be in the interval. If anything in the interval converges during this second run, a third is attempted and so on, until no more approximate eigenvalues θ_i show up inside. Then the algorithm signals convergence. If there are still unconverged approximate eigenvalues after a prescribed maximum number of steps, the algorithm signals nonconvergence and reports all solutions it has found.

This is a heuristic strategy that has worked well on both symmetric, nonsymmetric, and even defective eigenvalue problems. There is a tiny theoretical chance of missing an eigenvalue, if all the random starting vectors happen to be orthogonal to its eigenvector. Normally, the algorithm restarts p times, if the maximum multiplicity of an eigenvalue is p. At each restart a new random starting direction is introduced.

The shifted and inverted matrix A = (K – µM)^–1M is needed only to operate on a vector v_j in the Arnoldi algorithm. This is done by computing an LU factorization,

P(K – µM)Q = LU

using the sparse MATLAB^® command lu (P and Q are permutations that make the triangular factors L and U sparse and the factorization numerically stable). This factorization needs to be done only once, in the beginning, then x = Av_j is computed as,

x = QU^–1L^–1PMv_j

with one sparse matrix vector multiplication, a permutation, sparse forward- and back-substitutions, and a final renumbering.

Version History

Introduced before R2006a

collapse all

R2016a: Not recommended

pdeeig is not recommended. Use solvepdeeig instead. There are no plans to remove pdeeig.

pdeeig

Syntax

Description

Examples

Eigenvalues and Eigenvectors of L-Shaped Membrane

Eigenvalues and Eigenvectors of the L-Shaped Membrane Using Legacy Syntax

Eigenvalues and Eigenvectors Using Finite Element Matrices

Input Arguments

model — PDE model PDEModel object

c — PDE coefficient scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

a — PDE coefficient scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

d — PDE coefficient scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

r — Eigenvalue range two-element real vector

b — Boundary conditions boundary matrix | boundary file

p — Mesh points matrix

e — Mesh edges matrix

t — Mesh triangles matrix

Kc — Stiffness matrix sparse matrix | full matrix

B — Dirichlet nullspace sparse matrix

M — Mass matrix sparse matrix | full matrix

Output Arguments

v — Eigenvectors matrix

l — Eigenvalues vector

Limitations

Tips

Algorithms

Eigenvalue Equations

Version History

R2016a: Not recommended

See Also

`model` — PDE model
`PDEModel` object

`c` — PDE coefficient
scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

`a` — PDE coefficient
scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

`d` — PDE coefficient
scalar | matrix | character vector | character array | string scalar | string vector | coefficient function

`r` — Eigenvalue range
two-element real vector

`b` — Boundary conditions
boundary matrix | boundary file

`p` — Mesh points
matrix

`e` — Mesh edges
matrix

`t` — Mesh triangles
matrix

`Kc` — Stiffness matrix
sparse matrix | full matrix

`B` — Dirichlet nullspace
sparse matrix

`M` — Mass matrix
sparse matrix | full matrix

`v` — Eigenvectors
matrix

`l` — Eigenvalues
vector