Main Content

Bin Data to Create Credit Scorecards Using Binning Explorer

Create a credit scorecard using the Binning Explorer app. Use Binning Explorer to bin the data, plot the binned data information, and export a creditscorecard object or generate a function that creates a creditscorecard. Then use the creditscorecard object with functions from Financial Toolbox™ to fit a logistic regression model, determine a score for the data, determine the probabilities of default, and validate the credit scorecard model using three different metrics.

Step 1. Load credit scorecard data into the MATLAB workspace.

Use the CreditCardData.mat file to load the data into the MATLAB® workspace (using a data set from Refaat 2011). 

load CreditCardData
disp(data(1:10,:))
  CustID    CustAge    TmAtAddress    ResStatus     EmpStatus    CustIncome    TmWBank    OtherCC    AMBalance    UtilRate    status
    ______    _______    ___________    __________    _________    __________    _______    _______    _________    ________    ______

     1        53         62             Tenant        Unknown      50000         55         Yes        1055.9       0.22        0     
     2        61         22             Home Owner    Employed     52000         25         Yes        1161.6       0.24        0     
     3        47         30             Tenant        Employed     37000         61         No         877.23       0.29        0     
     4        50         75             Home Owner    Employed     53000         20         Yes        157.37       0.08        0     
     5        68         56             Home Owner    Employed     53000         14         Yes        561.84       0.11        0     
     6        65         13             Home Owner    Employed     48000         59         Yes        968.18       0.15        0     
     7        34         32             Home Owner    Unknown      32000         26         Yes        717.82       0.02        1     
     8        50         57             Other         Employed     51000         33         No         3041.2       0.13        0     
     9        50         10             Tenant        Unknown      52000         25         Yes        115.56       0.02        1     
    10        49         30             Home Owner    Unknown      53000         23         Yes         718.5       0.17        1

Step 2. Import the data into Binning Explorer.

Open Binning Explorer from the MATLAB toolstrip: On the Apps tab, under Computational Finance, click the app icon. Alternatively, you can enter binningExplorer on the MATLAB command line. For more information on starting Binning Explorer from the command line, see Start from MATLAB Command Line Using Data or an Existing creditscorecard Object.

From the Binning Explorer toolstrip, select Import Data to open the Import Data window.

Import Data dialog box

Under Step 1, select data.

Under Step 2, optionally set the Variable Type for each of the predictors. By default, the last column in the data ('status' in this example) is set to 'Response'. All other variables are considered predictors. However, in this example, because 'CustID' (customer identification number) is not a useful predictor, set the Variable Type column for 'CustID' to Do not include.

Note

If the input MATLAB table contains a column for weights, from the Step 2 pane, using the Variable Type column, click the drop-down to select Weights. For more information on using observation weights with a creditscorecard object, see Credit Scorecard Modeling Using Observation Weights.

If the data contains missing values, from the Step 2 pane, set Bin missing data: to Yes. For more information on working with missing data, see Credit Scorecard Modeling with Missing Values.

Under Step 3, leave Monotone as the default initial binning algorithm.

Click Import Data to complete the import operation. Automatic binning using the selected algorithm is applied to all predictors as they are imported into Binning Explorer.

The bins are plotted and displayed for each predictor. By clicking to select an individual predictor plot from the Overview pane, the details for that predictor plot display in the main pane and in the Bin Information and Predictor Information panes at the bottom of the app.

Predictor plots display after binning

Binning Explorer performs automatic binning for every predictor variable, using the default 'Monotone' algorithm with default algorithm options. A monotonic, ideally linear trend in the Weight of Evidence (WOE) is often desirable for credit scorecards because this translates into linear points for a given predictor. WOE trends are visualized on the plots for each predictor in Binning Explorer.

Perform some initial data exploration. Inquire about predictor statistics for the 'ResStatus' categorical variable.

Click the ResStatus plot. The Bin Information pane contains the “Good” and “Bad” frequencies and other bin statistics such as weight of evidence (WOE).

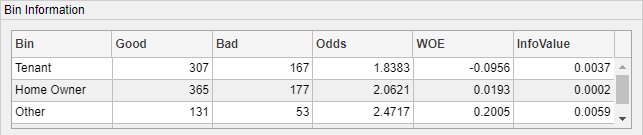
Bin information display

For numeric data, the same statistics are displayed. Click the CustIncome plot. The Bin Information is updated with the information about CustIncome.

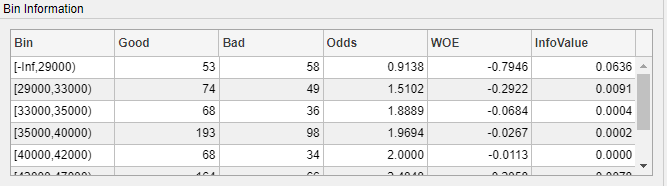
Bin information for CustIncome predictor

Step 3. Fine-tune the bins using manual binning in Binning Explorer.

Click the CustAge predictor plot. Notice that bins 1 and 2 have similar WOEs, as do bins 5 and 6.

Plot for CustAge predictor

To merge bins 1 and 2, from the main pane, click Ctrl + click or Shift + click to multiselect bin 1 and 2 to display with blue outlines for merging.

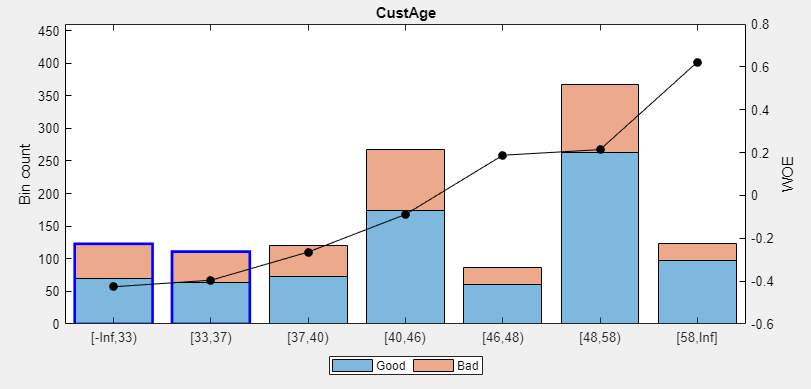
Plot for CustAge predictor with two bins selected

On the Binning Explorer toolstrip, use the read-only display for the Edges text boxes to verify values for the edges of the selected bins to merge.

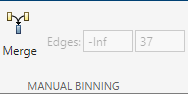
Use read-only Edges text box to verify selected bins for CustAge predictor

Click Merge to finish merging bins 1 and 2. The CustAge predictor plot is updated for the new bin information and the details in the Bin Information and Predictor Information panes are also updated.

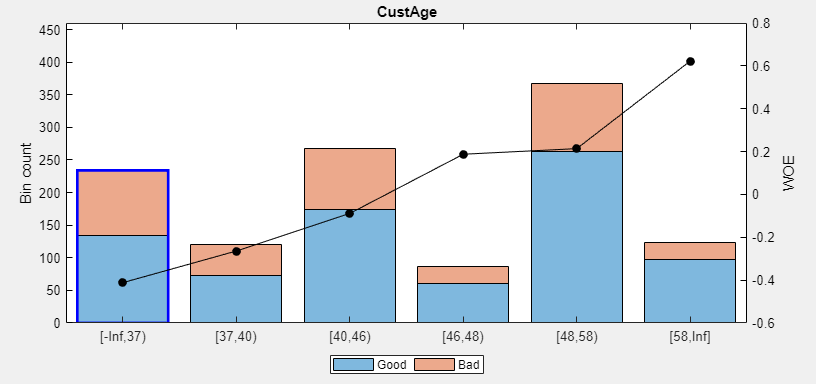
Plot for CustAge predictor with the two selected bins merged

Next, merge bins 4 and 5, because they also have similar WOEs.

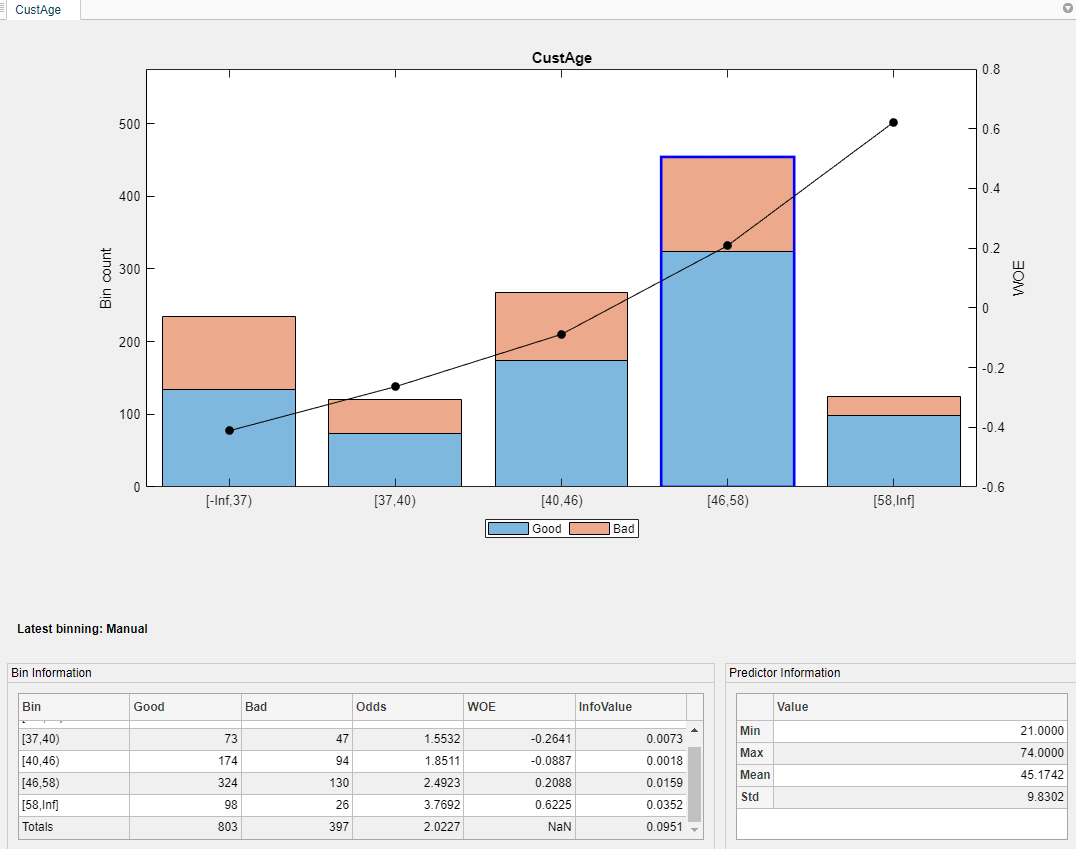
Plot for CustAge predictor with bins 4 and 5 selected for merging

The CustAge predictor plot is updated with the new bin information. The details in the Bin Information and Predictor Information panes are also updated.

Repeat this merge operation for the following bins that have similar WOEs:

  • For CustIncome, merge bins 3, 4 and 5.

  • For TmWBank, merge bins 2 and 3.

  • For AMBalance, merge bins 2 and 3.

Now the bins for all predictors have close-to-linear WOE trends.

Step 4. Export the creditscorecard object or generate a function that creates a creditscorecard object.

After you complete your binning assignments, using Binning Explorer, click Export and then click Export Scorecard and provide a creditscorecard object name. The creditscorecard object (sc) is saved to the MATLAB workspace.

Alternatively, click Export and then click Generate Function to create an untitled file in your editor. You can make any required modifications to the function, save it locally with an appropriate title, and call the function to create a creditscorecard object with the same binning assignments.

Step 5. Fit a logistic regression model.

Use the fitmodel function to fit a logistic regression model to the WOE data. fitmodel internally bins the training data, transforms it into WOE values, maps the response variable so that 'Good' is 1, and fits a linear logistic regression model. By default, fitmodel uses a stepwise procedure to determine which predictors belong in the model.

sc = fitmodel(sc);
1. Adding CustIncome, Deviance = 1490.8954, Chi2Stat = 32.545914, PValue = 1.1640961e-08
2. Adding TmWBank, Deviance = 1467.3249, Chi2Stat = 23.570535, PValue = 1.2041739e-06
3. Adding AMBalance, Deviance = 1455.858, Chi2Stat = 11.466846, PValue = 0.00070848829
4. Adding EmpStatus, Deviance = 1447.6148, Chi2Stat = 8.2432677, PValue = 0.0040903428
5. Adding CustAge, Deviance = 1442.06, Chi2Stat = 5.5547849, PValue = 0.018430237
6. Adding ResStatus, Deviance = 1437.9435, Chi2Stat = 4.1164321, PValue = 0.042468555
7. Adding OtherCC, Deviance = 1433.7372, Chi2Stat = 4.2063597, PValue = 0.040272676

Generalized Linear regression model:
    logit(status) ~ 1 + CustAge + ResStatus + EmpStatus + CustIncome + TmWBank + OtherCC + AMBalance
    Distribution = Binomial

Estimated Coefficients:
                   Estimate      SE       tStat       pValue  
                   ________    _______    ______    __________

    (Intercept)     0.7024       0.064    10.975    5.0407e-28
    CustAge        0.61562     0.24783    2.4841      0.012988
    ResStatus       1.3776     0.65266    2.1107      0.034799
    EmpStatus      0.88592     0.29296     3.024     0.0024946
    CustIncome     0.69836     0.21715     3.216     0.0013001
    TmWBank          1.106     0.23266    4.7538    1.9958e-06
    OtherCC         1.0933     0.52911    2.0662      0.038806
    AMBalance       1.0437     0.32292    3.2322     0.0012285


1200 observations, 1192 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 89.7, p-value = 1.42e-16

Step 6. Review and format scorecard points.

After fitting the logistic model, the points are unscaled by default and come directly from the combination of WOE values and model coefficients. Use the displaypoints function to summarize the scorecard points.

p1 = displaypoints(sc);
disp(p1)
    Predictors            Bin             Points  
    ____________    __________________    _________

    'CustAge'       '[-Inf,37)'            -0.15314
    'CustAge'       '[37,40)'             -0.062247
    'CustAge'       '[40,46)'              0.045763
    'CustAge'       '[46,58)'               0.22888
    'CustAge'       '[58,Inf]'              0.48354
    'ResStatus'     'Tenant'              -0.031302
    'ResStatus'     'Home Owner'            0.12697
    'ResStatus'     'Other'                 0.37652
    'EmpStatus'     'Unknown'             -0.076369
    'EmpStatus'     'Employed'              0.31456
    'CustIncome'    '[-Inf,29000)'         -0.45455
    'CustIncome'    '[29000,33000)'         -0.1037
    'CustIncome'    '[33000,42000)'        0.077768
    'CustIncome'    '[42000,47000)'         0.24406
    'CustIncome'    '[47000,Inf]'           0.43536
    'TmWBank'       '[-Inf,12)'            -0.18221
    'TmWBank'       '[12,45)'             -0.038279
    'TmWBank'       '[45,71)'               0.39569
    'TmWBank'       '[71,Inf]'              0.95074
    'OtherCC'       'No'                     -0.193
    'OtherCC'       'Yes'                   0.15868
    'AMBalance'     '[-Inf,558.88)'          0.3552
    'AMBalance'     '[558.88,1597.44)'    -0.026797
    'AMBalance'     '[1597.44,Inf]'        -0.21168

Use modifybins to give the bins more descriptive labels.

sc = modifybins(sc,'CustAge','BinLabels',...
{'Up to 36' '37 to 39' '40 to 45' '46 to 57' '58 and up'});

sc = modifybins(sc,'CustIncome','BinLabels',...
{'Up to 28999' '29000 to 32999' '33000 to 41999' '42000 to 46999' '47000 and up'});

sc = modifybins(sc,'TmWBank','BinLabels',...
{'Up to 11' '12 to 44' '45 to 70' '71 and up'});

sc = modifybins(sc,'AMBalance','BinLabels',...
{'Up to 558.87' '558.88 to 1597.43' '1597.44 and up'});

p1 = displaypoints(sc);
disp(p1)

     Predictors             Bin             Points  
    ____________    ___________________    _________

    'CustAge'       'Up to 36'              -0.15314
    'CustAge'       '37 to 39'             -0.062247
    'CustAge'       '40 to 45'              0.045763
    'CustAge'       '46 to 57'               0.22888
    'CustAge'       '58 and up'              0.48354
    'ResStatus'     'Tenant'               -0.031302
    'ResStatus'     'Home Owner'             0.12697
    'ResStatus'     'Other'                  0.37652
    'EmpStatus'     'Unknown'              -0.076369
    'EmpStatus'     'Employed'               0.31456
    'CustIncome'    'Up to 28999'           -0.45455
    'CustIncome'    '29000 to 32999'         -0.1037
    'CustIncome'    '33000 to 41999'        0.077768
    'CustIncome'    '42000 to 46999'         0.24406
    'CustIncome'    '47000 and up'           0.43536
    'TmWBank'       'Up to 11'              -0.18221
    'TmWBank'       '12 to 44'             -0.038279
    'TmWBank'       '45 to 70'               0.39569
    'TmWBank'       '71 and up'              0.95074
    'OtherCC'       'No'                      -0.193
    'OtherCC'       'Yes'                    0.15868
    'AMBalance'     'Up to 558.87'            0.3552
    'AMBalance'     '558.88 to 1597.43'    -0.026797
    'AMBalance'     '1597.44 and up'        -0.21168

Points are scaled and are also often rounded. To round and scale the points, use the formatpoints function. For example, you can set a target level of points corresponding to a target odds level and also set the required points-to-double-the-odds (PDO).

TargetPoints = 500;
TargetOdds = 2;
PDO = 50; % Points to double the odds

sc = formatpoints(sc,'PointsOddsAndPDO',[TargetPoints TargetOdds PDO]);
p2 = displaypoints(sc);
disp(p2)
    Predictors             Bin            Points
    ____________    ___________________    ______

    'CustAge'       'Up to 36'             53.239
    'CustAge'       '37 to 39'             59.796
    'CustAge'       '40 to 45'             67.587
    'CustAge'       '46 to 57'             80.796
    'CustAge'       '58 and up'            99.166
    'ResStatus'     'Tenant'               62.028
    'ResStatus'     'Home Owner'           73.445
    'ResStatus'     'Other'                91.446
    'EmpStatus'     'Unknown'              58.777
    'EmpStatus'     'Employed'             86.976
    'CustIncome'    'Up to 28999'          31.497
    'CustIncome'    '29000 to 32999'       56.805
    'CustIncome'    '33000 to 41999'       69.896
    'CustIncome'    '42000 to 46999'       81.891
    'CustIncome'    '47000 and up'          95.69
    'TmWBank'       'Up to 11'             51.142
    'TmWBank'       '12 to 44'             61.524
    'TmWBank'       '45 to 70'             92.829
    'TmWBank'       '71 and up'            132.87
    'OtherCC'       'No'                   50.364
    'OtherCC'       'Yes'                  75.732
    'AMBalance'     'Up to 558.87'         89.908
    'AMBalance'     '558.88 to 1597.43'    62.353
    'AMBalance'     '1597.44 and up'       49.016

Step 7. Score the data.

Use the score function to compute the scores for the training data. You can also pass an optional data input to score, for example, validation data. The points per predictor for each customer are provided as an optional output.

[Scores,Points] = score(sc);
disp(Scores(1:10))
disp(Points(1:10,:))
  528.2044
  554.8861
  505.2406
  564.0717
  554.8861
  586.1904
  441.8755
  515.8125
  524.4553
  508.3169

    CustAge    ResStatus    EmpStatus    CustIncome    TmWBank    OtherCC    AMBalance
    _______    _________    _________    __________    _______    _______    _________

    80.796     62.028       58.777        95.69        92.829     75.732     62.353   
    99.166     73.445       86.976        95.69        61.524     75.732     62.353   
    80.796     62.028       86.976       69.896        92.829     50.364     62.353   
    80.796     73.445       86.976        95.69        61.524     75.732     89.908   
    99.166     73.445       86.976        95.69        61.524     75.732     62.353   
    99.166     73.445       86.976        95.69        92.829     75.732     62.353   
    53.239     73.445       58.777       56.805        61.524     75.732     62.353   
    80.796     91.446       86.976        95.69        61.524     50.364     49.016   
    80.796     62.028       58.777        95.69        61.524     75.732     89.908   
    80.796     73.445       58.777        95.69        61.524     75.732     62.353

Step 8. Calculate the probability of default.

To calculate the probability of default, use the probdefault function. 

pd = probdefault(sc);

Define the probability of being “Good” and plot the predicted odds versus the formatted scores. Visually analyze that the target points and target odds match and that the points-to-double-the-odds (PDO) relationship holds.

ProbGood = 1-pd;
PredictedOdds = ProbGood./pd;

figure
scatter(Scores,PredictedOdds)
title('Predicted Odds vs. Score')
xlabel('Score')
ylabel('Predicted Odds')

hold on

xLimits = xlim;
yLimits = ylim;

% Target points and odds
plot([TargetPoints TargetPoints],[yLimits(1) TargetOdds],'k:')
plot([xLimits(1) TargetPoints],[TargetOdds TargetOdds],'k:')

% Target points plus PDO
plot([TargetPoints+PDO TargetPoints+PDO],[yLimits(1) 2*TargetOdds],'k:')
plot([xLimits(1) TargetPoints+PDO],[2*TargetOdds 2*TargetOdds],'k:')

% Target points minus PDO
plot([TargetPoints-PDO TargetPoints-PDO],[yLimits(1) TargetOdds/2],'k:')
plot([xLimits(1) TargetPoints-PDO],[TargetOdds/2 TargetOdds/2],'k:')

hold off

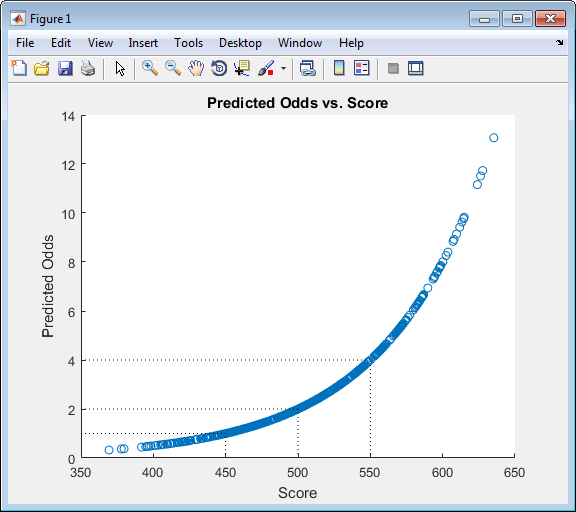
Plot for predicted odds versus score

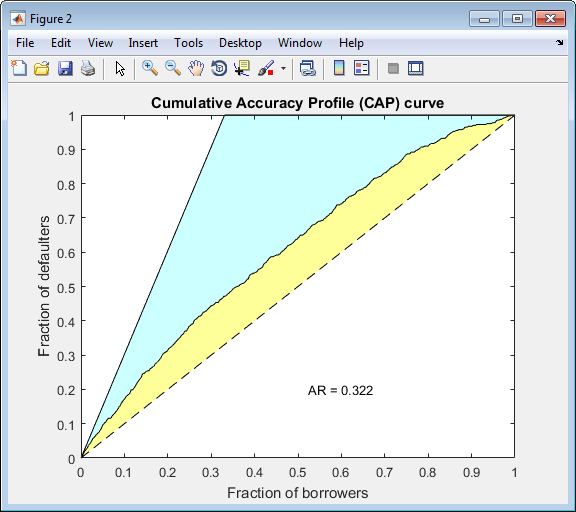
Step 9. Validate the credit scorecard model using the CAP, ROC, and Kolmogorov-Smirnov statistic

The creditscorecard object supports three validation methods, the Cumulative Accuracy Profile (CAP), the Receiver Operating Characteristic (ROC), and the Kolmogorov-Smirnov (KS) statistic. For more information on CAP, ROC, and KS, see validatemodel.

[Stats,T] = validatemodel(sc,'Plot',{'CAP','ROC','KS'});
disp(Stats)
disp(T(1:15,:))
          Measure             Value 
    ______________________    _______

    'Accuracy Ratio'          0.32225
    'Area under ROC curve'    0.66113
    'KS statistic'            0.22324
    'KS score'                 499.18

    Scores    ProbDefault    TrueBads    FalseBads    TrueGoods    FalseGoods    Sensitivity    FalseAlarm      PctObs  
    ______    ___________    ________    _________    _________    __________    ___________    __________    __________

     369.4     0.7535         0          1            802          397                   0      0.0012453     0.00083333
    377.86    0.73107         1          1            802          396           0.0025189      0.0012453      0.0016667
    379.78     0.7258         2          1            802          395           0.0050378      0.0012453         0.0025
    391.81    0.69139         3          1            802          394           0.0075567      0.0012453      0.0033333
    394.77    0.68259         3          2            801          394           0.0075567      0.0024907      0.0041667
    395.78    0.67954         4          2            801          393            0.010076      0.0024907          0.005
    396.95    0.67598         5          2            801          392            0.012594      0.0024907      0.0058333
    398.37    0.67167         6          2            801          391            0.015113      0.0024907      0.0066667
    401.26    0.66276         7          2            801          390            0.017632      0.0024907         0.0075
    403.23    0.65664         8          2            801          389            0.020151      0.0024907      0.0083333
    405.09    0.65081         8          3            800          389            0.020151       0.003736      0.0091667
    405.15    0.65062        11          5            798          386            0.027708      0.0062267       0.013333
    405.37    0.64991        11          6            797          386            0.027708       0.007472       0.014167
    406.18    0.64735        12          6            797          385            0.030227       0.007472          0.015
    407.14    0.64433        13          6            797          384            0.032746       0.007472       0.015833

CAP curve

ROC curve

K-S plot

See Also

| | | | | | | | | | | | | | | |

Related Examples

More About

External Websites