Create Custom Lifetime PD Model for Decision Tree Model with Function Handle

Open Live Script

This example shows how to fit a decision tree model for credit scoring and then use the customLifetimePDModel object to create a lifetime model for probability of default.

Fit a Decision Tree Model for Credit Scoring

Load the credit scorecard data using a data set from Refaat [1]. The data set in this example contains one row per loan.

load CreditCardData.mat
disp(head(data))

    CustID    CustAge    TmAtAddress    ResStatus     EmpStatus    CustIncome    TmWBank    OtherCC    AMBalance    UtilRate    status
    ______    _______    ___________    __________    _________    __________    _______    _______    _________    ________    ______

      1         53           62         Tenant        Unknown        50000         55         Yes       1055.9        0.22        0   
      2         61           22         Home Owner    Employed       52000         25         Yes       1161.6        0.24        0   
      3         47           30         Tenant        Employed       37000         61         No        877.23        0.29        0   
      4         50           75         Home Owner    Employed       53000         20         Yes       157.37        0.08        0   
      5         68           56         Home Owner    Employed       53000         14         Yes       561.84        0.11        0   
      6         65           13         Home Owner    Employed       48000         59         Yes       968.18        0.15        0   
      7         34           32         Home Owner    Unknown        32000         26         Yes       717.82        0.02        1   
      8         50           57         Other         Employed       51000         33         No        3041.2        0.13        0

Fit a decision tree model using fitctree from Statistics and Machine Learning Toolbox™. The data set in this example contains 1200 observations, which is not a large number. This example uses the data to train the model, but you can split larger data sets into training and testing sets.

CategoricalPreds = {'ResStatus','EmpStatus','OtherCC'};
dt = fitctree(data,'status~CustAge+TmAtAddress+ResStatus+EmpStatus+CustIncome+TmWBank+OtherCC+UtilRate', ...
    'MaxNumSplits',30,'CategoricalPredictors',CategoricalPreds);
disp(dt)

  ClassificationTree
           PredictorNames: {'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'UtilRate'}
             ResponseName: 'status'
    CategoricalPredictors: [3 4 7]
               ClassNames: [0 1]
           ScoreTransform: 'none'
          NumObservations: 1200

view(dt)

Decision tree for classification
 1  if CustIncome<30500 then node 2 elseif CustIncome>=30500 then node 3 else 0
 2  if TmWBank<60 then node 4 elseif TmWBank>=60 then node 5 else 1
 3  if TmWBank<32.5 then node 6 elseif TmWBank>=32.5 then node 7 else 0
 4  if TmAtAddress<13.5 then node 8 elseif TmAtAddress>=13.5 then node 9 else 1
 5  if UtilRate<0.255 then node 10 elseif UtilRate>=0.255 then node 11 else 0
 6  if CustAge<60.5 then node 12 elseif CustAge>=60.5 then node 13 else 0
 7  if CustAge<46.5 then node 14 elseif CustAge>=46.5 then node 15 else 0
 8  if CustIncome<24500 then node 16 elseif CustIncome>=24500 then node 17 else 1
 9  if TmWBank<56.5 then node 18 elseif TmWBank>=56.5 then node 19 else 1
10  if CustAge<21.5 then node 20 elseif CustAge>=21.5 then node 21 else 0
11  class = 1
12  if EmpStatus=Employed then node 22 elseif EmpStatus=Unknown then node 23 else 0
13  if TmAtAddress<131 then node 24 elseif TmAtAddress>=131 then node 25 else 0
14  if TmAtAddress<97.5 then node 26 elseif TmAtAddress>=97.5 then node 27 else 0
15  class = 0
16  class = 0
17  if ResStatus in {Home Owner Tenant} then node 28 elseif ResStatus=Other then node 29 else 1
18  if TmWBank<52.5 then node 30 elseif TmWBank>=52.5 then node 31 else 0
19  class = 1
20  class = 1
21  class = 0
22  if UtilRate<0.375 then node 32 elseif UtilRate>=0.375 then node 33 else 0
23  if UtilRate<0.005 then node 34 elseif UtilRate>=0.005 then node 35 else 0
24  if CustIncome<39500 then node 36 elseif CustIncome>=39500 then node 37 else 0
25  class = 1
26  if UtilRate<0.595 then node 38 elseif UtilRate>=0.595 then node 39 else 0
27  class = 1
28  class = 1
29  class = 0
30  class = 1
31  class = 0
32  class = 0
33  if UtilRate<0.635 then node 40 elseif UtilRate>=0.635 then node 41 else 0
34  if CustAge<49 then node 42 elseif CustAge>=49 then node 43 else 1
35  if CustIncome<57000 then node 44 elseif CustIncome>=57000 then node 45 else 0
36  class = 1
37  class = 0
38  class = 0
39  if CustIncome<34500 then node 46 elseif CustIncome>=34500 then node 47 else 1
40  class = 1
41  class = 0
42  class = 1
43  class = 0
44  class = 0
45  class = 1
46  class = 0
47  class = 1

The decision tree predict function returns a predicted class in the first output, where class = 0 means no-default, and class = 1 means default (same as the response data that you used to train the model). The predict function also returns the corresponding prediction scores or class probabilities as the second output.

In this example, you are interested in the probability of default, which is the class probability for class = 1 (the second column of the class probability output).

[~,ObservationClassProb] = predict(dt,data);
pdDT = ObservationClassProb(:,2);

Wrap Decision Tree Model as Lifetime PD Model

To wrap the decision tree model as a lifetime PD model, a function handle to a PD prediction function is required. For the decision tree in this example, the predict method of the decision tree does not return the PD values directly. Therefore, first create a helper function that takes the decision tree model and the data as inputs and returns the PD predictions. This helper function is implemented as myDTPredictFcn in Local Functions. Then define a function handle to this function, predictFcnHandle, that takes data as input and returns the PD.

predictFcnHandle = @(data)myDTPredictFcn(dt,data);

Create an instance of a custom lifetime PD model by passing the function handle to customLifetimePDModel. You need to specify variable names using name-value arguments because these variable names are used by the base class LifetimePDModel.

pdModel = customLifetimePDModel(predictFcnHandle,'ModelID','MyDTModel','IDVar','CustID','LoanVars',dt.PredictorNames,'ResponseVar',dt.ResponseName)

pdModel = 
  CustomLifetimePD with properties:

            ModelID: "MyDTModel"
        Description: ""
    UnderlyingModel: @(data)myDTPredictFcn(dt,data)
              IDVar: "CustID"
             AgeVar: ""
           LoanVars: ["CustAge"    "TmAtAddress"    "ResStatus"    "EmpStatus"    "CustIncome"    "TmWBank"    "OtherCC"    "UtilRate"]
          MacroVars: ""
        ResponseVar: "status"
         WeightsVar: ""
       TimeInterval: []

Predict and Validate Scores Using the Custom Lifetime PD Model

Use the predict function of the lifetime PD model to make PD predictions.

CondPD = predict(pdModel,data);

The predictions are the same as predicting directly with the original decision tree model.

CondPDOriginal = myDTPredictFcn(dt,data);
isequal(CondPD,CondPDOriginal)

ans = logical
   1

By wrapping the decision tree as a lifetime PD model, all the validation capabilities of lifetime PD models are available.

For example, use modelDiscriminationPlot to plot the ROC curve. The next plot shows the ROC curve for each of the residential status levels. All of the residential status levels show good discrimination in the training data.

modelDiscriminationPlot(pdModel,data,'SegmentBy','ResStatus')

Figure contains an axes object. The axes object with title ROC Segmented by ResStatus, xlabel Fraction of Non-Defaulters, ylabel Fraction of Defaulters contains 3 objects of type line. These objects represent MyDTModel, Home Owner, AUROC = 0.69519, MyDTModel, Tenant, AUROC = 0.69219, MyDTModel, Other, AUROC = 0.70603.

Also, you can use modelCalibrationPlot to visualize the calibration of the model. A grouping variable is required to compare the average PD for the group against the default rate in the group. For illustration purposes, define an AgeGroup variable. You can also use other variables, including model predictors, as grouping variables.

AgeGroupEdges = [0,20:5:65,100];
AgeGroupLabels = strcat(string(AgeGroupEdges(1:end-1))," - ",string(AgeGroupEdges(2:end)));
data.AgeGroup = discretize(data.CustAge,AgeGroupEdges,'categorical',AgeGroupLabels);
modelCalibrationPlot(pdModel,data,'AgeGroup')

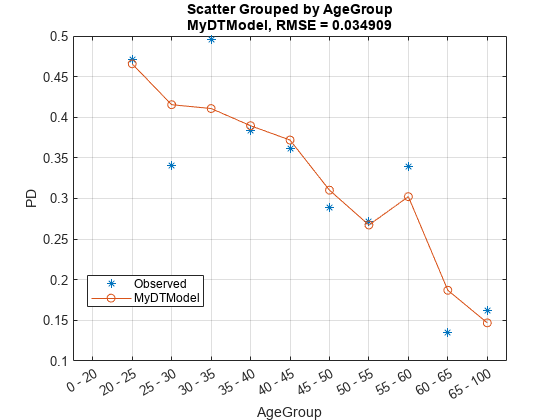
Figure contains an axes object. The axes object with title Scatter Grouped by AgeGroup MyDTModel, RMSE = 0.034909, xlabel AgeGroup, ylabel PD contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Observed, MyDTModel.

The default rates are high in this data set. The safest (60—65 and 65—100) age groups default at a rate higher than 10% and the 0—20 age group has a default rate of almost 50%. However, the predicted PDs are close to the observed default rates for most age groups. In other words, the model has good calibration in the training data.

Predict Lifetime PD

Lifetime PD is the cumulative probability of default over multiple periods. Therefore, the input for the predictLifetime function should contain multiple rows per ID. In this example, the data you use for training and validation contains only one observation per ID. If you pass it to predictLifetime, the output would be the same as the output of the predict function. For more information, see Lifetime PD and Data Input for Lifetime Prediction.

The predictLifetime function is typically used for predictions on outstanding loans, where the predictor variable values must be projected, period-by-period, for several periods into the future. To project predictor values to prepare data for lifetime prediction, suppose you have an existing customer with ID 1234, 35 years old, with 36 months in the current address, owns her house, is employed with an income of $75,000, a bank customer for 50 months, average monthly balance in the account is $895 dollars with a utilization rate of 27%, and does not have another credit card with the bank.

% Use first row as a template,
% removing response and age group.
dataLifetime = data(1,1:end-2);
dataLifetime.CustID = 1234;
dataLifetime.CustAge = 35;
dataLifetime.TmAtAddress = 36;
dataLifetime.ResStatus = 'Home Owner';
dataLifetime.EmpStatus = 'Employed';
dataLifetime.CustIncome = 75000;
dataLifetime.TmWBank = 50;
dataLifetime.OtherCC = 'No';
dataLifetime.AMBalance = 895;
dataLifetime.UtilRate = 0.27;
disp(dataLifetime)

    CustID    CustAge    TmAtAddress    ResStatus     EmpStatus    CustIncome    TmWBank    OtherCC    AMBalance    UtilRate
    ______    _______    ___________    __________    _________    __________    _______    _______    _________    ________

     1234       35           36         Home Owner    Employed       75000         50         No          895         0.27

To make projections for three periods ahead, you need projections for each variable. It is important to know what time interval is implicit in the underlying model because each PD model has a time interval. For more information, see Time Interval for Logistic Models and Time Interval and Data Input for Lifetime Prediction.

In this example, use the time interval of 1 year, in other words, assume that the decision tree model predicts 1-year PDs. In this case, age is easy to project because the customer is one year older on each subsequent time period, that is, on each subsequent row in the data. Other time variables, such as time at address and time with bank, are easily projected if you assume there will be no change in address and that the customer will continue with the bank. You can project other variables as well with assumptions for each of them. For example, for CustIncome, you can keep it constant, as in this example, where your assumption might be that the customer does not update their income information. Or, you could assume some income growth instead. In this example, for simplicity, all variables other than time variables, are kept constant.

dataLifetime = repmat(dataLifetime,3,1);
% No changes to the ID value, same customer
dataLifetime.CustAge(2:3) = dataLifetime.CustAge(1)+[1;2]; % one year older each year
dataLifetime.TmAtAddress(2:3) = dataLifetime.TmAtAddress(1)+[12; 24]; % 12 extra months each year
% No changes to ResStatus, EmpStatus or CustIncome
dataLifetime.TmWBank(2:3) = dataLifetime.TmWBank(1)+[12; 24]; % 12 extra months each year
% No changes to OtherCC, AMBalance or UtilRate
disp(dataLifetime)

    CustID    CustAge    TmAtAddress    ResStatus     EmpStatus    CustIncome    TmWBank    OtherCC    AMBalance    UtilRate
    ______    _______    ___________    __________    _________    __________    _______    _______    _________    ________

     1234       35           36         Home Owner    Employed       75000         50         No          895         0.27  
     1234       36           48         Home Owner    Employed       75000         62         No          895         0.27  
     1234       37           60         Home Owner    Employed       75000         74         No          895         0.27

Use predictLifetime to make a lifetime prediction.

pdLifetime = predictLifetime(pdModel,dataLifetime)

pdLifetime = 3×1

    0.2527
    0.4415
    0.5826

References

[1] Refaat, M. Credit Risk Scorecards: Development and Implementation Using SAS. lulu.com, 2011.

Local Functions

function CondPD = myDTPredictFcn(DTmodel,data)
%myDTPredictFcn Predict conditional PD with Decision Tree model.

[~,ObservationClassProb] = predict(DTmodel,data);
CondPD = ObservationClassProb(:,2);

end