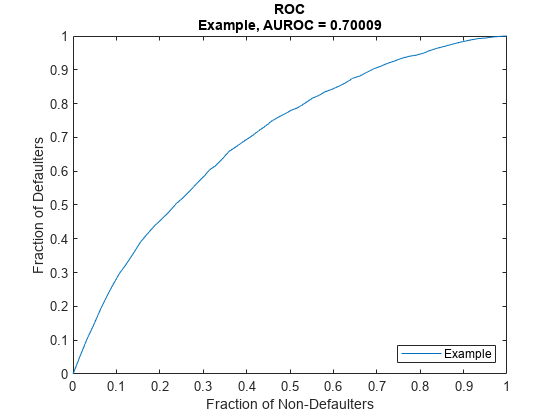
modelDiscriminationPlot
Syntax
Description
modelDiscriminationPlot(___,
specifies options using one or more name-value pair arguments in addition to the
input arguments in the previous syntax.Name,Value)
h = modelDiscriminationPlot(ax,___,Name,Value)h.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
References
[1] Baesens, Bart, Daniel Roesch, and Harald Scheule. Credit Risk Analytics: Measurement Techniques, Applications, and Examples in SAS. Wiley, 2016.
[2] Bellini, Tiziano. IFRS 9 and CECL Credit Risk Modelling and Validation: A Practical Guide with Examples Worked in R and SAS. San Diego, CA: Elsevier, 2019.
[3] Breeden, Joseph. Living with CECL: The Modeling Dictionary. Santa Fe, NM: Prescient Models LLC, 2018.
[4] Roesch, Daniel and Harald Scheule. Deep Credit Risk: Machine Learning with Python. Independently published, 2020.
Version History
Introduced in R2021aSee Also
predictLifetime | predict | modelDiscrimination | modelCalibration | modelCalibrationPlot | fitLifetimePDModel | Logistic | Probit | Cox | customLifetimePDModel
Topics
- Basic Lifetime PD Model Validation
- Compare Logistic Model for Lifetime PD to Champion Model
- Compare Lifetime PD Models Using Cross-Validation
- Expected Credit Loss Computation
- Compare Model Discrimination and Model Calibration to Validate of Probability of Default
- Compare Probability of Default Using Through-the-Cycle and Point-in-Time Models
- Overview of Lifetime Probability of Default Models