Cox
Description
Create and analyze a Cox model object to calculate
lifetime probability of default (PD) using this workflow:
Use
fitLifetimePDModelto create aCoxmodel object.Optionally, use
discardResidualsto remove residual information from theCoxmodel object.Use
predictto predict the conditional PD andpredictLifetimeto predict the lifetime PD.Use
modelDiscriminationto return AUROC and ROC data. You can plot the results usingmodelDiscriminationPlot.Use
modelCalibrationto return the root mean square error (RMSE) of observed and predicted PD data. You can plot the results usingmodelCalibrationPlot.
Creation
Syntax
Description
CoxPDModel = fitLifetimePDModel(data,ModelType,AgeVar=agevar_value)Cox PD model object.
If you do not specify variable information for
IDVar, LoanVars,
MacroVars, and
ResponseVar, then:
IDVaris set to the first column in thedatainput.LoanVarsis set to include all columns from the second to the second-to-last columns of thedatainput.ResponseVaris set to the last column in thedatainput.
CoxPDModel = fitLifetimePDModel(___,Name=Value)CoxPDModel =
fitLifetimePDModel(data(TrainDataInd,:),"Cox",ModelID="Cox_A",Description="Cox_model",AgeVar="YOB",IDVar="ID",LoanVars="ScoreGroup",MacroVars={'GDP','Market'},ResponseVar="Default",TimeInterval=1,TieBreakMethod="Efron",WeightsVar="Weights")
creates a CoxPDModel using a Cox model
type. You can specify multiple name-value arguments.
Input Arguments
Data, specified as a table, in panel data form. The data must
contain an ID column and an
Age column. The response variable must be a
binary variable with the value 0 or
1, with 1 indicating
default.
Data Types: table
Model type, specified as a string with the value
"Cox" or a character vector with the value
'Cox'.
Data Types: char | string
Name-Value Arguments
Specify required
and optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where
Name is the argument name and Value is
the corresponding value. Name-value arguments must appear after other arguments,
but the order of the pairs does not matter.
Example: CoxPDModel =
fitLifetimePDModel(data(TrainDataInd,:),"Cox",ModelID="Cox_A",Description="Cox_model",AgeVar="YOB",IDVar="ID",LoanVars="ScoreGroup",MacroVars={'GDP','Market'},ResponseVar="Default",TimeInterval=1,WeightsVar="Weights")
Required Cox Name-Value Argument
Age variable indicating which column in
data contains the loan age information,
specified as AgeVar and a string or character vector.
Note
The required name-value argument AgeVar
is not treated as a predictor in the Cox
lifetime PD model. When using a Cox
model, you must specify predictor variables using
LoanVars or
MacroVars. The
AgeVar values are the event times for
the underlying Cox proportional hazards model.
AgeVar values for each ID should be
increasing. If there are nonpositive age increments,
fitLifetimePDModel warns when you create a
Cox model and removes the IDs with
nonpositive age increments. By default, the
TimeInterval value is set to the
most common age increment in the training data.
Data Types: string | char
Optional Cox Name-Value Arguments
User-defined model ID, specified as ModelID
and a string or character vector. The software uses the
ModelID to format outputs and is expected to
be short.
Data Types: string | char
User-defined description for model, specified as
Description and a string or character
vector.
Data Types: string | char
ID variable indicating which column in
data contains the loan or borrower ID,
specified as IDVar and a string or character
vector.
Data Types: string | char
Loan variables indicating which column in
data contains the loan-specific
information, such as origination score or loan-to-value ratio,
specified as LoanVars and a string array or cell
array of character vectors.
Data Types: string | cell
Macro variables indicating which column in
data contains the macroeconomic
information, such as gross domestic product (GDP) growth or
unemployment rate, specified as MacroVars and a
string array or cell array of character vectors.
Data Types: string | cell
Variable indicating which column in data
contains the response variable, specified as
ResponseVar and a logical value.
Note
The response variable values in the
data must be a binary variable with
0 or 1 values,
with 1 indicating default.
In Cox lifetime PD models, the
ResponseVar values define the
censoring information for the underlying Cox proportional
hazards model.
Data Types: string | char
Column name of the input table containing weights, specified as a string scalar.
Note
The default value ("") results in a weight
of 1 for each row in data.
All weight values in data must be
nonnegative.
For an example using WeightsVar, see Create Weighted Lifetime PD Model.
Data Types: string
Time interval value, specified as a positive numeric scalar
indicating the time interval used to define the 0-1 default
indicator values in the response variable. The time interval
typically coincides with the distance between age values in training
data in the panel data input. For example, if
the age data (AgeVar) is 1, 2, 3, ..., then the
TimeInterval is 1; if the
age data is 0.25, 0.5, 0.75,..., then the
TimeInterval is 0.25. For
more information, see Time Interval for Cox Models and Lifetime Prediction and Time Interval. For Cox models, the
TimeInterval value is necessary to fit
time-dependent models and also for the PD computation when you use
the predict function.
Note
Unlike Logistic and Probit
models, a Cox model requires an
AgeVar variable. By default, if you
do not specify a TimeInterval when
creating a Cox model, the
TimeInterval is inferred from the
increments in the AgeVar values in the
training data.
Data Types: double
Since R2023a
Method to handle tied default times, specified as a string or character vector with one of the following tie-break methods:
breslow— Breslow's approximation to the partial likelihoodefron— Efron's approximation to the partial likelihood
For credit applications, the time to default comes discretized and
there are many "ties." This means that are multiple borrowers that
may default at the same (discretized) time (such as, in the second
year of their loan). TieBreakMethod supports the
breslow or efron methods
to handle this scenario.
Data Types: string | char
Properties
User-defined model ID, returned as a string.
Data Types: string
User-defined description, returned as a string.
Data Types: string
ID variable indicating which column in data
contains the loan or borrower ID, returned as a string.
Data Types: string
Age variable indicating which column in data
contains the loan age information, returned as a string.
Data Types: string
Loan variables indicating which column in data
contains the loan-specific information, returned as a string
array.
Data Types: string
Macro variables indicating which column in data
contains the macroeconomic information, returned as a string
array.
Data Types: string
Variable indicating which column in data contains
the response variable, returned as a string.
Data Types: string
Column name of the input table containing weights, returned as a string scalar.
Data Types: string
This property is read-only.
Time interval value, returned as a positive numeric scalar.
Data Types: double
Extrapolation factor, returned as a positive numeric scalar between
0 and 1.
By default, the ExtrapolationFactor is set to
1. For age values (AgeVar)
greater than the maximum age observed in the training data, the
conditional PD, computed with predict,
uses the maximum age observed in the training data. In particular, the
predicted PD value is constant if the predictor values do not change and
only the age values change when the
ExtrapolationFactor is 1. For
more information, see Extrapolation for Cox Models, Extrapolation Factor for Cox Models, and Use Cox Lifetime PD Model to Predict Conditional PD.
Data Types: double
Method to handle tied default times, returned as a string.
Data Types: string
Object Functions
predict | Compute conditional PD |
predictLifetime | Compute cumulative lifetime PD, marginal PD, and survival probability |
modelDiscrimination | Compute AUROC and ROC data |
modelCalibration | Compute RMSE of predicted and observed PDs on grouped data |
modelDiscriminationPlot | Plot ROC curve |
modelCalibrationPlot | Plot observed default rates compared to predicted PDs on grouped data |
discardResiduals | Discard residual information of underlying Cox model |
Examples
This example shows how to use fitLifetimePDModel to create a Cox model using credit and macroeconomic data.
Load Data
Load the credit portfolio data.
load RetailCreditPanelData.mat
disp(head(data)) ID ScoreGroup YOB Default Year
__ __________ ___ _______ ____
1 Low Risk 1 0 1997
1 Low Risk 2 0 1998
1 Low Risk 3 0 1999
1 Low Risk 4 0 2000
1 Low Risk 5 0 2001
1 Low Risk 6 0 2002
1 Low Risk 7 0 2003
1 Low Risk 8 0 2004
disp(head(dataMacro))
Year GDP Market
____ _____ ______
1997 2.72 7.61
1998 3.57 26.24
1999 2.86 18.1
2000 2.43 3.19
2001 1.26 -10.51
2002 -0.59 -22.95
2003 0.63 2.78
2004 1.85 9.48
Join the two data components into a single data set.
data = join(data,dataMacro); disp(head(data))
ID ScoreGroup YOB Default Year GDP Market
__ __________ ___ _______ ____ _____ ______
1 Low Risk 1 0 1997 2.72 7.61
1 Low Risk 2 0 1998 3.57 26.24
1 Low Risk 3 0 1999 2.86 18.1
1 Low Risk 4 0 2000 2.43 3.19
1 Low Risk 5 0 2001 1.26 -10.51
1 Low Risk 6 0 2002 -0.59 -22.95
1 Low Risk 7 0 2003 0.63 2.78
1 Low Risk 8 0 2004 1.85 9.48
Partition Data
Separate the data into training and test partitions.
nIDs = max(data.ID); uniqueIDs = unique(data.ID); rng('default'); % For reproducibility c = cvpartition(nIDs,'HoldOut',0.4); TrainIDInd = training(c); TestIDInd = test(c); TrainDataInd = ismember(data.ID,uniqueIDs(TrainIDInd)); TestDataInd = ismember(data.ID,uniqueIDs(TestIDInd));
Create a Cox Lifetime PD Model
Use fitLifetimePDModel to create a Cox model using the training data.
pdModel = fitLifetimePDModel(data(TrainDataInd,:),"Cox",... AgeVar="YOB", ... IDVar="ID", ... LoanVars="ScoreGroup", ... MacroVars={'GDP','Market'}, ... ResponseVar="Default"); disp(pdModel)
Cox with properties:
ExtrapolationFactor: 1
ModelID: "Cox"
Description: ""
UnderlyingModel: [1×1 CoxModel]
IDVar: "ID"
AgeVar: "YOB"
LoanVars: "ScoreGroup"
MacroVars: ["GDP" "Market"]
ResponseVar: "Default"
WeightsVar: ""
TimeInterval: 1
Display the underlying model.
disp(pdModel.UnderlyingModel)
Cox Proportional Hazards regression model
Beta SE zStat pValue
__________ _________ _______ ___________
ScoreGroup_Medium Risk -0.6794 0.037029 -18.348 3.4442e-75
ScoreGroup_Low Risk -1.2442 0.045244 -27.501 1.7116e-166
GDP -0.084533 0.043687 -1.935 0.052995
Market -0.0084411 0.0032221 -2.6198 0.0087991
Log-likelihood: -41742.871
Validate Model
Use modelDiscrimination to measure the ranking of customers by PD.
DataSetChoice ="Testing"; if DataSetChoice=="Training" Ind = TrainDataInd; else Ind = TestDataInd; end DiscMeasure = modelDiscrimination(pdModel,data(Ind,:),SegmentBy="ScoreGroup")
DiscMeasure=3×1 table
AUROC
_______
Cox, ScoreGroup=High Risk 0.64112
Cox, ScoreGroup=Medium Risk 0.61989
Cox, ScoreGroup=Low Risk 0.6314
disp(DiscMeasure)
AUROC
_______
Cox, ScoreGroup=High Risk 0.64112
Cox, ScoreGroup=Medium Risk 0.61989
Cox, ScoreGroup=Low Risk 0.6314
Use modelDiscriminationPlot to visualize the ROC curve.
modelDiscriminationPlot(pdModel,data(Ind,:),SegmentBy="ScoreGroup")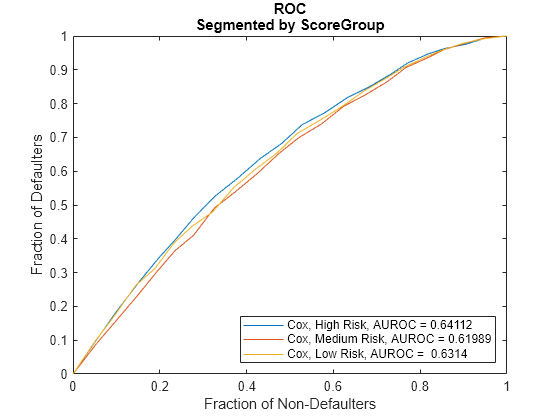
Use modelCalibration to measure the calibration of the predicted PD values. The modelCalibration function requires a grouping variable and compares the accuracy of the observed default rate in the group with the average predicted PD for the group.
CalMeasure = modelCalibration(pdModel,data(Ind,:),{'YOB','ScoreGroup'})CalMeasure=table
RMSE
_________
Cox, grouped by YOB, ScoreGroup 0.0012471
disp(CalMeasure)
RMSE
_________
Cox, grouped by YOB, ScoreGroup 0.0012471
Use modelCalibrationPlot to visualize the observed default rates compared to the predicted PD.
modelCalibrationPlot(pdModel,data(Ind,:),{'YOB','ScoreGroup'})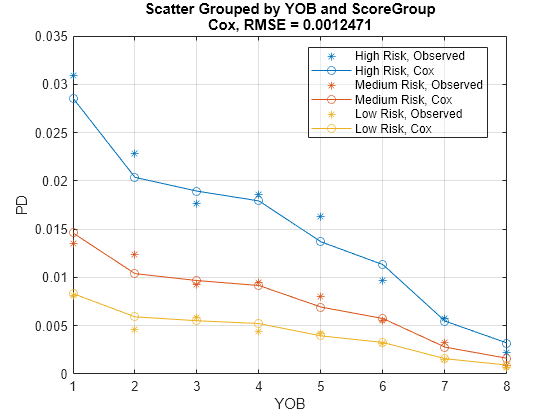
Predict Conditional and Lifetime PD
Use the predict function to predict conditional PD values. The prediction is a row-by-row prediction.
%dataCustomer1 = data(1:8,:);
CondPD = predict(pdModel,data(Ind,:));Use predictLifetime to predict the lifetime cumulative PD values (computing marginal and survival PD values is also supported).
LifetimePD = predictLifetime(pdModel,data(Ind,:));
Since R2023a
This example shows how to create a Cox model and select the tie-break method while fitting a Cox lifetime PD model.
Load Data
Load the credit portfolio data.
load RetailCreditPanelData.mat
disp(head(data)) ID ScoreGroup YOB Default Year
__ __________ ___ _______ ____
1 Low Risk 1 0 1997
1 Low Risk 2 0 1998
1 Low Risk 3 0 1999
1 Low Risk 4 0 2000
1 Low Risk 5 0 2001
1 Low Risk 6 0 2002
1 Low Risk 7 0 2003
1 Low Risk 8 0 2004
disp(head(dataMacro))
Year GDP Market
____ _____ ______
1997 2.72 7.61
1998 3.57 26.24
1999 2.86 18.1
2000 2.43 3.19
2001 1.26 -10.51
2002 -0.59 -22.95
2003 0.63 2.78
2004 1.85 9.48
Join the two data components into a single data set.
data = join(data,dataMacro); disp(head(data))
ID ScoreGroup YOB Default Year GDP Market
__ __________ ___ _______ ____ _____ ______
1 Low Risk 1 0 1997 2.72 7.61
1 Low Risk 2 0 1998 3.57 26.24
1 Low Risk 3 0 1999 2.86 18.1
1 Low Risk 4 0 2000 2.43 3.19
1 Low Risk 5 0 2001 1.26 -10.51
1 Low Risk 6 0 2002 -0.59 -22.95
1 Low Risk 7 0 2003 0.63 2.78
1 Low Risk 8 0 2004 1.85 9.48
Join the Data
Join the two data components into a single data set.
data = join(data,dataMacro); disp(head(data))
ID ScoreGroup YOB Default Year GDP Market
__ __________ ___ _______ ____ _____ ______
1 Low Risk 1 0 1997 2.72 7.61
1 Low Risk 2 0 1998 3.57 26.24
1 Low Risk 3 0 1999 2.86 18.1
1 Low Risk 4 0 2000 2.43 3.19
1 Low Risk 5 0 2001 1.26 -10.51
1 Low Risk 6 0 2002 -0.59 -22.95
1 Low Risk 7 0 2003 0.63 2.78
1 Low Risk 8 0 2004 1.85 9.48
Partition the Data
Separate the data into training and test partitions.
nIDs = max(data.ID); uniqueIDs = unique(data.ID); rng('default'); % for reproducibility c = cvpartition(nIDs,'HoldOut',0.4); TrainIDInd = training(c); TestIDInd = test(c); TrainDataInd = ismember(data.ID,uniqueIDs(TrainIDInd)); TestDataInd = ismember(data.ID,uniqueIDs(TestIDInd));
Create a Cox Lifetime PD Model with Breslow's Method
Use fitLifetimePDModel to create a Cox model using the training data. Use the name-value argument TieBreakMethod to set tie-break method to 'breslow'. This is the default choice for this argument.
pdModel1 = fitLifetimePDModel(data(TrainDataInd,:),"Cox",... ModelID="Cox-Breslow", IDVar="ID", AgeVar="YOB", ... LoanVars="ScoreGroup", MacroVars={'GDP','Market'}, ... ResponseVar="Default",TieBreakMethod='breslow');
Display the underlying model.
disp(pdModel1.Model)
Cox Proportional Hazards regression model
Beta SE zStat pValue
__________ _________ _______ ___________
ScoreGroup_Medium Risk -0.6794 0.037029 -18.348 3.4442e-75
ScoreGroup_Low Risk -1.2442 0.045244 -27.501 1.7116e-166
GDP -0.084533 0.043687 -1.935 0.052995
Market -0.0084411 0.0032221 -2.6198 0.0087991
Log-likelihood: -41742.871
Use predict to predict the conditional PD.
pd1 = predict(pdModel1,data(TestDataInd,:));
Create a Cox Lifetime PD Model with Efron's Method
Use fitLifetimePDModel to create a Cox model using the training data. Use the name-value argument TieBreakMethod to set tie-break method to 'Efron'. This is the default choice for this argument.
pdModel2 = fitLifetimePDModel(data(TrainDataInd,:),"Cox",... ModelID="Cox-Efron", IDVar="ID", AgeVar="YOB", ... LoanVars="ScoreGroup", MacroVars={'GDP','Market'}, ... ResponseVar="Default",TieBreakMethod='efron');
Display the underlying model. The coefficients are only slightly different for this data set.
disp(pdModel2.Model)
Cox Proportional Hazards regression model
Beta SE zStat pValue
__________ _________ _______ __________
ScoreGroup_Medium Risk -0.6844 0.037029 -18.483 2.8461e-76
ScoreGroup_Low Risk -1.2515 0.045243 -27.662 2.006e-168
GDP -0.084985 0.043691 -1.9452 0.051756
Market -0.0085126 0.0032223 -2.6418 0.0082469
Log-likelihood: -41713.445
Use predict to predict the conditional PD for the second Cox model.
pd2 = predict(pdModel2,data(TestDataInd,:));
Compare Cox Models
The predictions for the two Cox models are almost the same for this data set.
[pd1(1:10) pd2(1:10)]
ans = 10×2
0.0162 0.0161
0.0091 0.0090
0.0081 0.0081
0.0073 0.0072
0.0064 0.0064
0.0072 0.0072
0.0030 0.0030
0.0016 0.0016
0.0162 0.0161
0.0091 0.0090
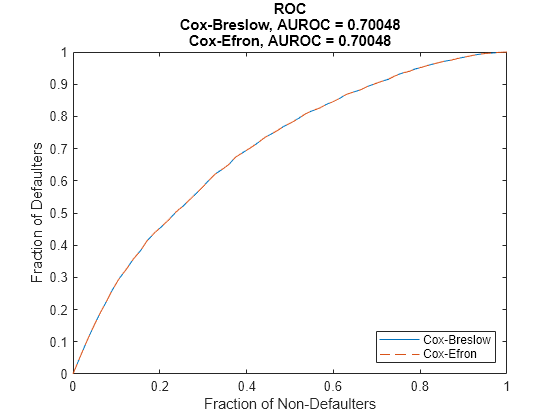
For this data set, the model discrimination (modelDiscrimination) does not seem to change with the TieBreakMethod method and the model accuracy (modelCalibration) shows only a negligible difference in RMSE.
modelDiscriminationPlot(pdModel1,data(TestDataInd,:),ReferencePD=pd2,ReferenceID=pdModel2.ModelID)
modelCalibrationPlot(pdModel1,data(TestDataInd,:),'Year',ReferencePD=pd2,ReferenceID=pdModel2.ModelID)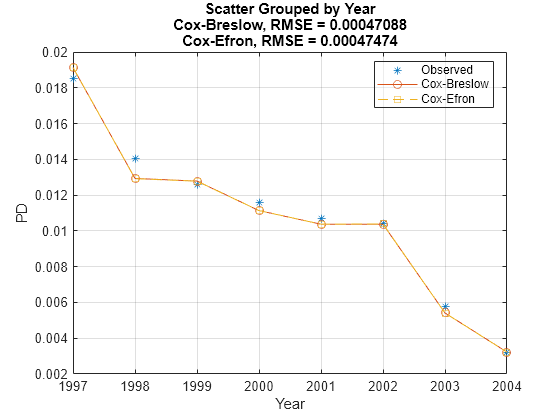
More About
The Cox proportional hazards (PH) model is a survival model and it models the time until an event of interest occurs.
For probability of default (PD) models, the event of interest is the default
on a credit obligation. Cox models need information on
whether there was a default and when it happened. For other commonly used PD
models, a binary variable indicating whether there was a default is enough.
Cox PD models need that information, plus the age of the
loan at the time of default.
The Cox proportional hazards (PH) model, also known as a
Cox regression model, assumes the hazard rate is of the form
where
h0(t) is the baseline hazard rate.
X is the predictor data.
β is a vector of coefficients of the predictors.
exp(Xβ) is the hazard ratio.
The baseline hazard rate is a reference hazard level, common to all
observations, and it does not depend on the predictor values. The hazard ratio
is the factor that scales the baseline hazard value up or down, depending on the
predictor values. For lower risk observations, the hazard ratio is less than
1 and this reduces the hazard rate. For higher risk
observations, the hazard ratio increases the hazard rate.
In the hazard rate formula, the predictor values in X are
fixed, or independent of time. This is the
basic version of the Cox PH model. For PD models, the basic
version of the Cox PH model includes predictors that have
constant values, such as the origination score, or whether a property is for
residential or commercial purposes.
The time-dependent
Cox PH model allows predictor values to change over time. For
example, the loan-to-value (LTV) ratio changes over the life of a loan, and the
macroeconomic variables change from period to period. Therefore, the following
hazard rate formula for time-dependent models includes predictor values that can
be a function of time:
The data input for fitLifetimePDModel must be in panel data form. For each ID
(IDVar), there are multiple rows of data. The panel
data input is required for both time-dependent and time
-independent models.
For time-independent predictors, the predictor value is constant for each ID.
For example, the score at origination for each customer is constant throughout
the life of the loan, and this value is repeated for each row corresponding to
the same ID in the panel data format.
For time-dependent predictors, the values may change from one row to the next
for the same ID. The assumption is that the predictor values in each row are
valid in the time interval defined by the age value
(AgeVar) in the previous row and the age value in the
current row.
Time is discretized into intervals, and predictor values in
the training data (data input) are constant for each
interval: X1 from
t0 to
t1;
X2 from
t1 to
t2; and so forth.
The data input must be in panel data form, with multiple
observations for each ID, with corresponding age information (the
tk values, the
AgeVar column) and the corresponding default indicator
values (the ResponseVar column).
Assume that tk -
tk - 1 =
Δt for all k and this is the
time interval. This time interval is the age increment
for consecutive observations in the age data (AgeVar). The
assumption is that these increments are regular and that the default indicator
(ResponseVar) is defined consistently with this time
interval, in the sense that a 1 means there was a default in a
time interval of length Δt. The time interval
Δt is also used for the computation of the probability of
default. For more information, see Survival and Probability of Default for Cox Models. The
TimeInterval property is also used to validate the data input
to predictLifetime; for more information see Validation of Data Input for Lifetime Prediction and Lifetime Prediction and Time Interval.
The survival function S(t) is a function of time, and gives the probability of surviving longer than a given time t.
where
T is the failure time, the random variable of interest, and in the
Coxmodel case, the time to default.t is the specific time of interest, for example, 1 year.
The main relationship between the survival function and the hazard rate is
Higher values of the hazard rate cause the survival probability to drop faster. Conversely, lower values of the hazard rate cause the survival probability to rise faster.
The probability of default (PD) is the conditional probability of defaulting in a time interval, given that there has been no default prior to that interval. For example, the probability of default between time s and t, with s < t, is represented as:
In credit applications, the time interval of interest, Δt, is consistent with the training data and the definition of default in the response variable. The PD is a function of a single time variable t and the implicit time interval Δt:
References
[1] Baesens, Bart, Daniel Roesch, and Harald Scheule. Credit Risk Analytics: Measurement Techniques, Applications, and Examples in SAS. Wiley, 2016.
[2] Bellini, Tiziano. IFRS 9 and CECL Credit Risk Modelling and Validation: A Practical Guide with Examples Worked in R and SAS. San Diego, CA: Elsevier, 2019.
[3] Breeden, Joseph. Living with CECL: The Modeling Dictionary. Santa Fe, NM: Prescient Models LLC, 2018.
[4] Roesch, Daniel and Harald Scheule. Deep Credit Risk: Machine Learning with Python. Independently published, 2020.
Version History
Introduced in R2021bThe Cox model supports a WeightsVar
name-value argument for observation weights.
The modelAccuracy object function is renamed to
modelCalibration function. The use of
modelAccuracy is discouraged, use modelCalibration instead.
The modelAccuracyPlot object function is renamed to
modelCalibrationPlot function. The use of
modelAccuracyPlot is discouraged, use modelCalibrationPlot
instead.
The TieBreakMethod name-value argument enables you to specify
the method to handle tied default times.
Use the discardResiduals
method to discard residual information of the underlying Cox model.
The Model property is renamed to
UnderlyingModel.
See Also
Functions
Topics
- Basic Lifetime PD Model Validation
- Compare Logistic Model for Lifetime PD to Champion Model
- Compare Lifetime PD Models Using Cross-Validation
- Expected Credit Loss Computation
- Compare Model Discrimination and Model Calibration to Validate of Probability of Default
- Compare Probability of Default Using Through-the-Cycle and Point-in-Time Models
- Modeling Probabilities of Default with Cox Proportional Hazards
- Create Weighted Lifetime PD Model
- Overview of Lifetime Probability of Default Models
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)