Estimate Pose of Fixed Camera Relative to Robot Base

This example uses:

In pick-and-place tasks, such as bin picking, it is common for cameras to be mounted to a fixed position in the environment to enable robot manipulators detect the objects in the workspace. The essential perception pipeline uses this camera to estimate the pose of a target object relative to the camera frame. This pose is then transformed to the base frame of the robot, enabling the robot to successfully pick the object with the end effector. To transform the pose of the object to the robot base frame, you must first determine the pose of the camera with respect to the robot base. This figure shows this kind of pick-and-place configuration and the desired homogeneous transformation matrix, TCameraToBase, which transforms poses in the camera frame to the robot base frame.

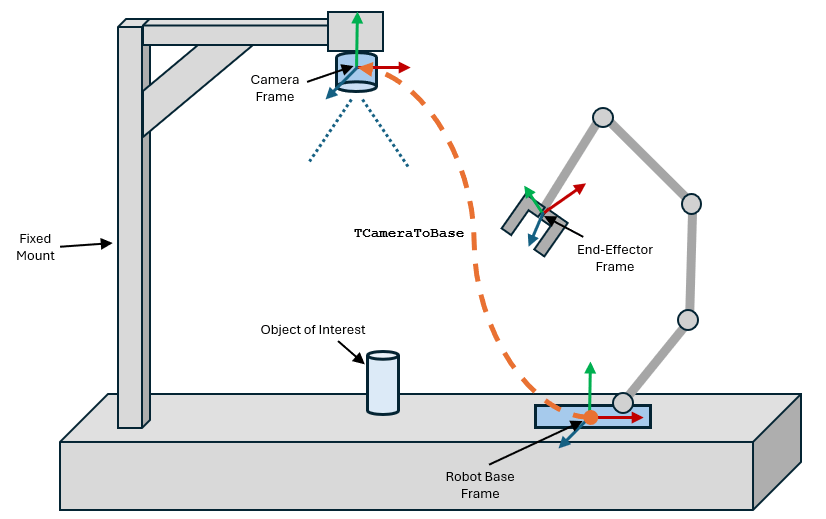
Robot pick-and-place setup with fixed camera pose

Determining the exact pose of the camera frame presents challenges due to these factors:

Camera manufacturers usually do not mark the camera frame directly on the device, nor do they provide specifications or physical indicators for it. Moreover, the frame relevant for pick-and-place operations is not the camera frame itself but rather a frame situated at the center of the image sensor or plane.
Estimations that assume the camera frame is centered around the lens and rely on manual measurements with a ruler are prone to inaccuracies.

Given these challenges outlined, this example shows the process of determining the transformation matrix, the pose of the camera mounted on a beam relative to the robot's base, by employing the hand-eye calibration workflow.

This example is related to the Perform Hand-in-Eye Calibration for Robot Arm with Camera example, which shows the calibration process for a robot arm with a camera mounted directly on the robot arm, known as Hand-in-Eye configuration. This example shows how to solve for the camera calibration problem for the Eye-to-Hand configuration.

Estimate Camera Intrinsics

Understanding the intrinsic parameters of the camera, such as its focal length and optical center, is crucial for accurately interpreting images. This example provides the camera intrinsics for this setup in the estimateCameraPoseWrtRobotBase.mat file. However for a different camera and setup, you must determine the camera intrinsics before collecting hand-eye calibration data. You can use the Camera Calibrator (Computer Vision Toolbox) app to estimate these parameters for a fixed camera. For more details about how to use this app, see Using the Single Camera Calibrator App (Computer Vision Toolbox).

Collect Hand-Eye Calibration Data

To collect the calibration data for hand-to-eye configurations, you must follow these steps:

Mount the calibration board on the end effector of the robot.
Move the robot to a configuration in which the calibration board pattern is fully visible to the mounted camera.
Capture the image of the calibration board from the camera and record the corresponding joint configuration of the robot.
Repeat Steps 1-3 to collect at least 15 such images and the corresponding robot joint configurations.

For this example setup, the calibration data has already been collected in the calibrationData.zip file. It contains both the calibration images and the corresponding robot joint configurations.

Unzip the calibration data and display all the calibration images.

unzip("calibrationData.zip")
calibimgds = imageDatastore('calibrationData/*.jpg');
figure(Name="Calibration Images")
montage(calibimgds);

Figure Calibration Images contains an axes object. The hidden axes object contains an object of type image.

Load and display the corresponding joint configurations from the jointAngles.mat file. The row number of each joint configuration aligns with the name of the corresponding calibration image. For example, the 10th row of jointAngles corresponds to calibration image 10.jpg. The joint angles are measured in degrees.

load("calibrationData/jointAngles")
disp(jointAngles)

  346.8241  352.5997  191.5695  212.1722  355.5775   38.5151  184.8700
  346.8241  352.5996  191.5695  212.1724  355.5776   20.6987  184.8699
  346.8241  352.5996  191.5695  212.1723  355.5775   55.1762  184.8699
  346.8241  352.5996  191.5695  212.1723  355.5775   55.1761  159.7137
  344.9588  352.5997  191.5695  212.1723  355.5775   47.9125  202.4223
  344.9591  350.7478  191.5696  212.1723  334.9004   43.3278  191.6003
  344.9592  350.7479  191.5696  212.1722   22.5804   43.3278  191.6003
  344.9592  350.7477  191.5696  212.1723   14.6105   17.6080  191.6004
  344.9592  350.7478  191.5696  212.1723   65.1178   27.7940  121.8693
    9.4972  350.7477  191.5696  212.1723   65.1178   27.7940  121.8693
    2.4139  356.8379  179.3088  225.4389   79.5231   35.3008  125.8531
   15.2262  356.8380  179.3092  225.4386   48.9265   55.5291  125.8531
   15.2261    4.5792  179.3092  225.4386   48.9264   55.5291  175.2737
   31.0168    4.5793  179.3092  225.4386   48.9263   55.5291  174.4471
   34.9532  358.5155  179.3093  225.4386   48.9264   55.5294  145.9294

To visualize the robot in a certain joint configuration, load the corresponding robot model and visualize the robot model with the desired joint configuration.

Load the rigid body tree robot model for the KINOVA® Gen3 robot and visualize it in the 7th joint configuration.

figure
kinova = loadrobot('kinovaGen3',DataFormat="row");
show(kinova,deg2rad(jointAngles(7,:)));
title("Joint Angles in 7th Configuration")
axis equal

Compute Camera Extrinsics and End-Effector Poses

The hand-to-eye calibration problem requires several sets of poses. Each set comprises two poses:

1. The camera extrinsics, which is the pose of the checkerboard's origin with respect to the camera.

2. The end-effector pose with respect to the robot base frame.

You can derive both of these poses using the calibration images and the corresponding joint configurations.

Estimate Camera Extrinsics

First calculate the camera extrinsics, the homogeneous transformation matrix, TWorldToCamera.

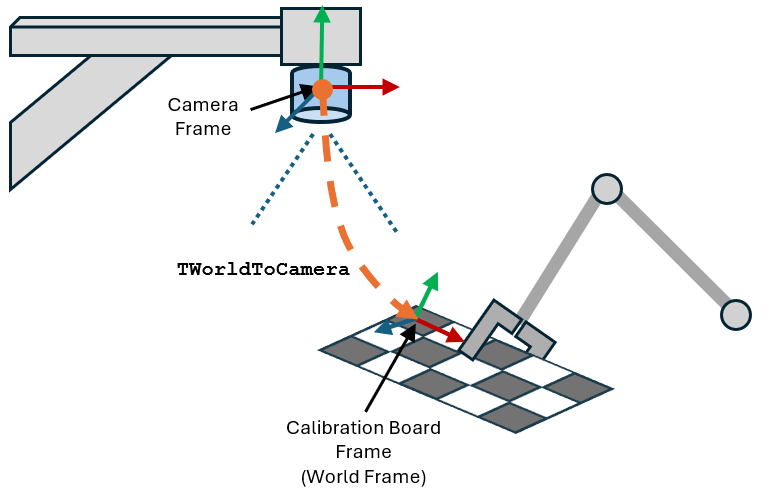
Transformation from world frame to the camera frame.

Create the camextrinsics vector for storing the camera extrinsics of each calibration image.

numimgs = length(calibimgds.Files);
camextrinsics = repmat(rigidtform3d,1,numimgs);

Before you can estimate the camera extrinsics, you must determine the intrinsic parameters of the camera and the size of the checkerboard squares in each calibration image. In this example, both the intrinsic parameters and the size of the checkerboard squares have already been computed. For more information about computing the camera intrinsics, see the Single Camera Calibration example on the estimateCameraParameters (Computer Vision Toolbox) function page.

Load the camera intrinsic parameters and the checkerboard square size.

load("estimateCameraPoseWrtRobotBase","intrinsics");
load("estimateCameraPoseWrtRobotBase","checkerboardSquareSizeInMeters");

For each image in your dataset, calculate the camera extrinsics. This estimation requires the calibration image, corrected for any distortion, and the position of the checkerboard points in the world frame. Then use these data to estimate the pose of the camera.

for r = 1:numimgs

    % Load and undistort each calibration image based on precomputed intrinsics.
    fname = fullfile('calibrationData',string(r)+".jpg");
    checkerboardImage = imread(fname);
    checkerboardImageUndistorted = undistortImage(checkerboardImage,intrinsics);

    % Detect the checkerboard corners, discarding partial detections.
    [imgpts,boardsz] = detectCheckerboardPoints(checkerboardImageUndistorted,PartialDetections=false);

    % Generate world coordinates of checkerboard points based on board size and square size.
    worldpts = patternWorldPoints("checkerboard",boardsz,checkerboardSquareSizeInMeters);

    % Estimate the camera extrinsics (pose) from image points and world points.
    camextrinsics(r) = estimateExtrinsics(imgpts,worldpts,intrinsics);
end

Compute End-Effector Poses

Next, use forward kinematics to calculate the pose of the end effector of the robot with respect to the base frame of the robot. The homogeneous transformation matrix representing this pose is TEndEffectorToBase.

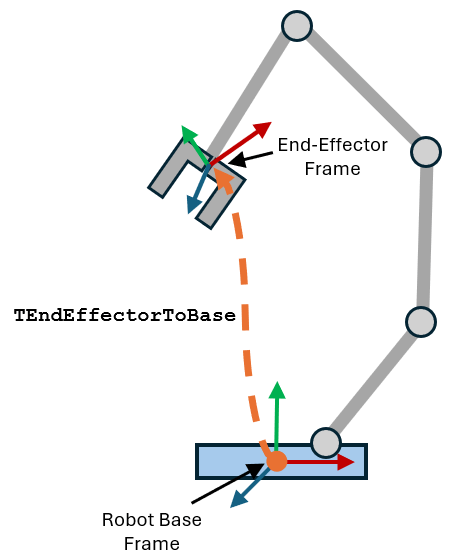
Transformation from end effector frame to the robot base frame.

Record the end-effector poses with respect to the robot base frame in TEndEffectorToBase vector.

TEndEffectorToBase = repmat(rigidtform3d,1,numimgs);

For each joint configuration, apply forward kinematics by using the getTransform function. This calculates the pose of the "EndEffector_Link" body of the robot with respect to the base frame of the robot.

for r = 1:numimgs
    jointconfig = deg2rad(jointAngles(r,:));
    TEndEffectorToBase(r) = getTransform(kinova,jointconfig,"EndEffector_Link");
end

Solve Calibration Problem

With the camera extrinsics and end-effector poses from the calibration data, estimate the pose of the camera with respect to the base of the robot.

TCameraToBase = helperEstimateHandEyeTransform(camextrinsics,TEndEffectorToBase,"eye-to-hand");

Next, calculate the position of the calibration checkerboard points with respect to the robot base frame.

TWorldToBase = rigidtform3d(TCameraToBase.A*camextrinsics(end).A);
worldpts3d = transformPointsForward(TWorldToBase,[worldpts,zeros(size(worldpts,1),1)]);

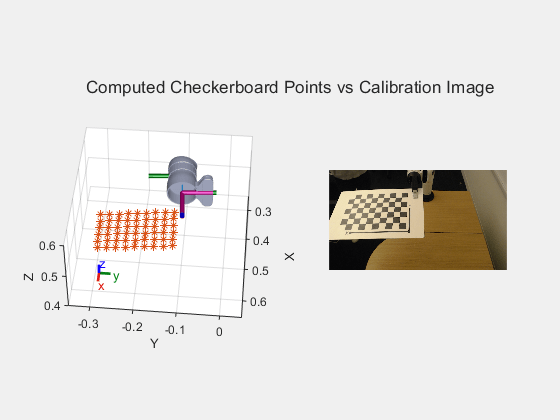
Visualize the robot with the checkerboard points and zoom in to compare it to the calibration image.

tiledlayout(1,2)
nexttile
show(kinova,deg2rad(jointAngles(r,:)));
hold on
scatter3(worldpts3d(:,1),worldpts3d(:,2),worldpts3d(:,3),'*')
view(95,45)
axis([-0.05 0.95 -0.65 0.35 0.25 0.75])
zoom(2.5)
hold off
nexttile
imshow("calibrationData/"+string(r)+".jpg")
sgtitle("Computed Checkerboard Points vs Calibration Image")

Visualize Camera Frame Relative to Robot Base Frame

Plot the camera, robot, and the checkerboard grid points resolved in the robot base frame.

figure
show(kinova,deg2rad(jointAngles(r,:)));
hold on
scatter3(worldpts3d(:,1),worldpts3d(:,2),worldpts3d(:,3),'*')
plotCamera(AbsolutePose=TCameraToBase,Size=0.05,Label="Fixed Camera");
title("Estimated Camera Frame With Respect to Robot Base")
view([-40,10])
zoom(1.5)
axis equal
hold off

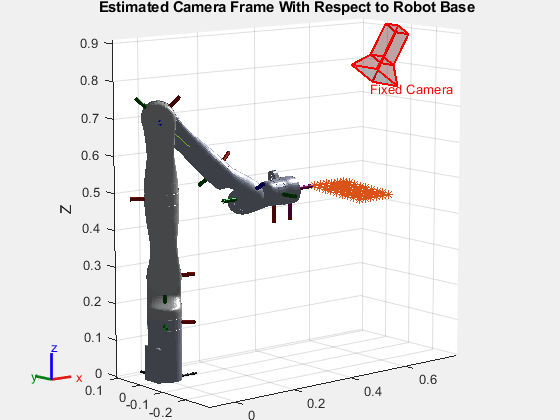
Comparing with the real setup shows that the estimated camera pose, with respect to the robot base, is correct.

Copyrights 2024 The MathWorks, Inc.