dksyn

(Not recommended) Robust controller design for discrete-time plants using µ-synthesis

dksyn is not recommended. Use musyn instead. For more information, see Version History.

Syntax

[k,clp,bnd] = dksyn(p,nmeas,ncont)
[k,clp,bnd] = dksyn(p,nmeas,ncont,opt)
[k,clp,bnd,dkinfo] = dksyn(p,nmeas,ncont,...)
[k,clp,bnd,dkinfo] = dksyn(p,nmeas,ncont,prevdkinfo,opt)
 [...] = dksyn(p)

Description

[k,clp,bnd] = dksyn(p,nmeas,ncont) synthesizes a robust controller k for the uncertain open-loop plant model p via the D-K or D-G-K algorithm for µ-synthesis. p is an uncertain state-space uss model. The last nmeas outputs and ncont inputs of p are assumed to be the measurement and control channels. k is the controller, clp is the closed-loop model and bnd is the robust closed-loop performance bound. p, k, clp, and bnd are related as follows:

        clp = lft(p,k); 
        bnd1 = dksynperf(clp); 
        bnd = 1/bnd1.LowerBound;

[k,clp,bnd] = dksyn(p,nmeas,ncont,opt) specifies user-defined options opt for the D-K or D-K-G algorithm. Use dksynOptions to create opt.

[k,clp,bnd,dkinfo] = dksyn(p,nmeas,ncont,...) returns a log of the algorithm execution in dkinfo. dkinfo is an N-by-1 cell array where N is the total number of iterations performed. The ith cell contains a structure with the following fields:

Field	Description
`K`	Controller at `i`th iteration, a `ss` object
`Bnds`	Robust performance bound on the closed-loop system (`double`)
`DL`	Left D-scale, an `ss` object
`DR`	Right D-scale, an `ss` object
`GM`	Offset G-scale, an `ss` object
`GR`	Right G-scale, an `ss` object
`GFC`	Center G-scale, an `ss` object
`MussvBnds`	Upper and lower µ bounds, an `frd` object
`MussvInfo`	Structure returned from `mussv` at each iteration.

[k,clp,bnd,dkinfo] = dksyn(p,nmeas,ncont,prevdkinfo,opt) allows you to use information from a previous dksyn iteration. prevdkinfo is a structure from a previous attempt at designing a robust controller using dksyn. prevdkinfo is used when the dksyn starting iteration is not 1 (opt.StartingIterationNumber = 1) to determine the correct D-scalings to initiate the iteration procedure.

[...] = dksyn(p) takes p as a uss object that has two-input/two-output partitioning as defined by mktito.

Examples

The following statements create a robust performance control design for an unstable, uncertain single-input/single-output plant model. The nominal plant model, G, is an unstable first order system $\frac{s}{s - 1}$ .

G = tf(1,[1 -1]);

The model itself is uncertain. At low frequency, below 2 rad/s, it can vary up to 25% from its nominal value. Around 2 rad/s the percentage variation starts to increase and reaches 400% at approximately 32 rad/s. The percentage model uncertainty is represented by the weight Wu which corresponds to the frequency variation of the model uncertainty and the uncertain LTI dynamic object InputUnc.

Wu = 0.25*tf([1/2 1],[1/32 1]); 
InputUnc = ultidyn('InputUnc',[1 1]);

The uncertain plant model Gpert represents the model of the physical system to be controlled.

Gpert = G*(1+InputUnc*Wu);

The robust stability objective is to synthesize a stabilizing LTI controller for all the plant models parameterized by the uncertain plant model, Gpert. The performance objective is defined as a weighted sensitivity minimization problem. The control interconnection structure is shown in the following figure.

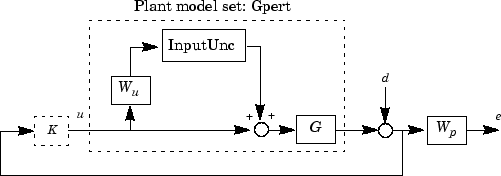
The sensitivity function, S, is defined as

$S = \frac{1}{1 + P K}$

where P is the plant model and K is the controller. A weighted sensitivity minimization problem selects a weight Wp, which corresponds to the inverse of the desired sensitivity function of the closed-loop system as a function of frequency. Hence the product of the sensitivity weight Wp and actual closed-loop sensitivity function is less than 1 across all frequencies. The sensitivity weight Wp has a gain of 100 at low frequency, begins to decrease at 0.006 rad/s, and reaches a minimum magnitude of 0.25 after 2.4 rad/s.

Wp = tf([1/4 0.6],[1 0.006]);

The defined sensitivity weight Wp implies that the desired disturbance rejection should be at least 100:1 disturbance rejection at DC, rise slowly between 0.006 and 2.4 rad/s, and allow the disturbance rejection to increase above the open-loop level, 0.25, at high frequency.

When the plant model is uncertain, the closed-loop performance objective is to achieve the desired sensitivity function for all plant models defined by the uncertain plant model, Gpert. The performance objective for an uncertain system is a robust performance objective. A block diagram of this uncertain closed-loop system illustrating the performance objective (closed-loop transfer function from d→e) is shown.

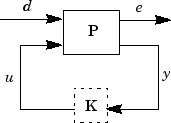
From the definition of the robust performance control objective, the weighted, uncertain control design interconnection model, which includes the robustness and performance objectives, can be constructed and is denoted by P. The robustness and performance weights are selected such that if the robust performance structure singular value, bnd, of the closed-loop uncertain system, clp, is less than 1 then the performance objectives have been achieved for all the plant models in the model set.

You can form the uncertain transfer matrix P from [d; u] to [e; y] using the following commands.

P = [Wp; 1 ]*[1 Gpert]; 
[K,clp,bnd] = dksyn(P,1,1); 
bnd

bnd = 
    0.6806

The controller K achieves a robust performance µ value bnd of about 0.68. Therefore you have achieved the robust performance objectives for the given problem.

You can use the robgain command to analyze the closed-loop robust performance of clp.

[rpmarg,rpmargunc] = robgain(clp,1);

Limitations

There are two shortcomings of the D-K iteration control design procedure:

Calculation of the structured singular value µΔ(·) is approximated by its upper bound. This is not a serious problem because the value of µ and its upper bound are often close.
The D-K iteration is not guaranteed to converge to a global, or even local minimum. This is a serious problem, and represents the biggest limitation of the design procedure.

In spite of these drawbacks, the D-K iteration control design technique appears to work well on many engineering problems. It has been applied to a number of real-world applications with success. These applications include vibration suppression for flexible structures, flight control, chemical process control problems, and acoustic reverberation suppression in enclosures.

Algorithms

collapse all

dksyn synthesizes a robust controller via D-K iteration. The D-K iteration procedure is an approximation to µ-synthesis control design. The objective of µ-synthesis is to minimize the structure singular value µ of the corresponding robust performance problem associated with the uncertain system p. The uncertain system p is an open-loop interconnection containing known components including the nominal plant model, uncertain parameters, ucomplex, and unmodeled LTI dynamics, ultidyn, and performance and uncertainty weighting functions. You use weighting functions to include magnitude and frequency shaping information in the optimization. The control objective is to synthesize a stabilizing controller k that minimizes the robust performance µ value, which corresponds to bnd.

The D-K iteration procedure involves a sequence of minimizations, first over the controller variable K (holding the D variable associated with the scaled µ upper bound fixed), and then over the D variable (holding the controller K variable fixed). The D-K iteration procedure is not guaranteed to converge to the minimum µ value, but often works well in practice.

dksyn automates the D-K iteration procedure and the options object dksynOptions allows you to customize its behavior. Internally, the algorithm works with the generalized scaled plant model P, which is extracted from a uss object using the command lftdata.

The following is a list of what occurs during a single, complete step of the D-K iteration.

(In the first iteration, this step is skipped.) The µ calculation (from the previous step) provides a frequency-dependent scaling matrix, D_f. The fitting procedure fits these scalings with rational, stable transfer function matrices. After fitting, plots of
$\bar{σ} ({\hat{D}}_{f} (j ω) F_{L} (P, K) (j ω) D_{f}^{- 1} (j ω))$
and
$\bar{σ} ({\hat{D}}_{f} (j ω) F_{L} (P, K) (j ω) {\hat{D}}_{f}^{- 1} (j ω))$
are shown for comparison.
(In the first iteration, this step is skipped.) The rational $\hat{D}$ is absorbed into the open-loop interconnection for the next controller synthesis. Using either the previous frequency-dependent D's or the just-fit rational $\hat{D}$ , an estimate of an appropriate value for the H_∞ norm is made. This is simply a conservative value of the scaled closed-loop H_∞ norm, using the most recent controller and either a frequency sweep (using the frequency-dependent D's) or a state-space calculation (with the rational D's).
(The first iteration begins at this point.) A controller is designed using H_∞ synthesis on the scaled open-loop interconnection. If you set the DisplayWhileAutoIter field in dksynOptions to 'on', the following information is displayed:
1. The progress of the γ-iteration is displayed.
2. The singular values of the closed-loop frequency response are plotted.
3. You are given the option to change the frequency range. If you change it, all relevant frequency responses are automatically recomputed.
4. You are given the option to rerun the H_∞ synthesis with a set of modified parameters if you set the AutoIter field in dksynOptions to 'off'. This is convenient if, for instance, the bisection tolerance was too large, or if maximum gamma value was too small.
The structured singular value of the closed-loop system is calculated and plotted.
An iteration summary is displayed, showing all the controller order, as well as the peak value of µ of the closed-loop frequency responses.
The choice of stopping or performing another iteration is given.

Subsequent iterations proceed along the same lines without the need to reenter the iteration number. A summary at the end of each iteration is updated to reflect data from all previous iterations. This often provides valuable information about the progress of the robust controller synthesis procedure.

Interactive Fitting of D-Scalings

Setting the AutoIter field in dksynOptions to 'off' requires that you interactively fit the D-scales each iteration. During step 2 of the D-K iteration procedure, you are prompted to enter your choice of options for fitting the D-scaling data. You press return after, the following is a list of your options.

Enter Choice (return for list): 
  Choices:
		nd	Move to Next D-scaling
		nb	Move to Next D-Block
		i	Increment Fit Order
		d	Decrement Fit Order
		apf	Auto-PreFit
		mx 3	Change Max-Order to 3
		at 1.01	Change Auto-Prefit Tol to 1.01
		0	Fit with zeroth order
		2	Fit with second order
		n	Fit with n'th order
		e	Exit with Current Fittings
		s	See Status

nd and nb allow you to move from one D-scale data to another. nd moves to the next scaling, whereas nb moves to the next scaling block. For scalar D-scalings, these are identical operations, but for problems with full D-scalings, (perturbations of the form δI) they are different. In the (1,2) subplot window, the title displays the D-scaling block number, the row/column of the scaling that is currently being fitted, and the order of the current fit (with d for data when no fit exists).
You can increment or decrement the order of the current fit (by 1) using i and d.
apf automatically fits each D-scaling data. The default maximum state order of individual D-scaling is 5. The mx variable allows you to change the maximum D-scaling state order used in the automatic prefitting routine. mx must be a positive, nonzero integer. at allows you to define how close the rational, scaled µ upper bound is to approximate the actual µ upper bound in a norm sense. Setting at to 1 would require an exact fit of the D-scale data, and is not allowed. Allowable values for at are greater than 1. This setting plays a role (mildly unpredictable, unfortunately) in determining where in the (D,K) space the D-K iteration converges.
Entering a positive integer at the prompt will fit the current D-scale data with that state order rational transfer function.
e exits the D-scale fitting to continue the D-K iteration.
The variable s displays a status of the current and fits.

References

[1] Balas, G.J., and J.C. Doyle, “Robust control of flexible modes in the controller crossover region,” AIAA Journal of Guidance, Dynamics and Control, Vol. 17, no. 2, March-April, 1994, p. 370-377.

[2] Balas, G.J., A.K. Packard, and J.T. Harduvel, “Application of µ-synthesis techniques to momentum management and attitude control of the space station,” AIAA Guidance, Navigation and Control Conference, New Orleans, August 1991.

[3] Doyle, J.C., K. Lenz, and A. Packard, “Design examples using µ-synthesis: Space shuttle lateral axis FCS during reentry,” NATO ASI Series, Modelling, Robustness, and Sensitivity Reduction in Control Systems, vol. 34, Springer-Verlag, Berlin 1987.

[4] Packard, A., J. Doyle, and G. Balas, “Linear, multivariable robust control with a µ perspective,” ASME Journal of Dynamic Systems, Measurement and Control, 50th Anniversary Issue, Vol. 115, no. 2b, June 1993, p. 310-319.

[5] Stein, G., and J. Doyle, “Beyond singular values and loopshapes,” AIAA Journal of Guidance and Control, Vol. 14, No. 1, January, 1991, p. 5-16.

Version History

Introduced before R2006a