Main Content

risetime

Rise time of positive-going bilevel waveform transitions

collapse all in page

Syntax

r = risetime(x)
r = risetime(x,fs)
r = risetime(x,t)
[r,lt,ut] = risetime(___)
[r,lt,ut,ll,ul] = risetime(___)
[___] = risetime(___,Name=Value)
risetime(___)

Description

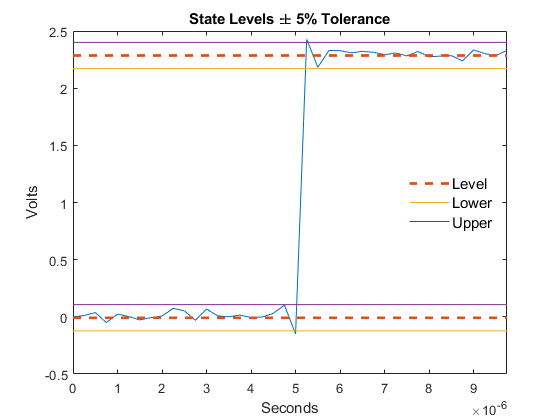
r = risetime(x) returns a vector, r, containing the time each transition of the input bilevel waveform, x, takes to cross from the 10% to 90% reference levels. To determine the transitions, risetime estimates the state levels of the input waveform by a histogram method. risetime identifies all regions that cross the upper-state boundary of the low state and the lower-state boundary of the high state. The low-state and high-state boundaries are expressed as the state level plus or minus a multiple of the difference between the state levels. See State-Level Tolerances. Because risetime uses interpolation, r can contain values that do not correspond to sampling instants of the bilevel waveform, x.

example

r = risetime(x,fs) specifies the sample rate in hertz. The sample rate determines the sample instants corresponding to the elements in x. The first sample instant in x corresponds to t = 0. Because risetime uses interpolation, r can contain values that do not correspond to sampling instants of the bilevel waveform, x.

example

r = risetime(x,t) specifies the sample instants, t, as a vector with the same number of elements as x.

[r,lt,ut] = risetime(___) returns vectors lt and ut whose elements correspond to the time instants where x crosses the lower- and upper-percent reference levels. You can use this output syntax with any of the previous input syntaxes.

example

[r,lt,ut,ll,ul] = risetime(___) returns the levels, ll and ul, that correspond to the lower- and upper-percent reference levels.

example

[___] = risetime(___,Name=Value) returns the rise times with additional options specified by one or more name-value arguments.

example

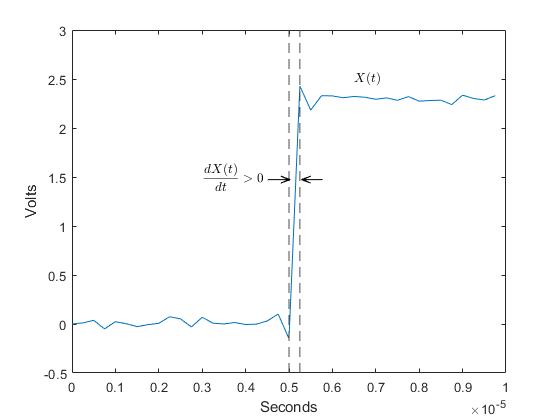
risetime(___) plots the signal and darkens the regions of each transition where rise time is computed. The plot marks the lower and upper crossings and the associated reference levels. The state levels and the corresponding associated lower- and upper-state boundaries are also plotted.

Examples

collapse all

Open Live Script

Determine the rise time in samples for a 2.3 V clock waveform.

Load the 2.3 V clock data. Determine the rise time in samples. Use the default 10% and 90% percent reference levels.

load("transitionex.mat","x","t")
R = risetime(x)
R = 
0.7120

The rise time is less than 1, indicating that the transition occurred in a fraction of a sample. Plot the data, including the time information, and annotate the rise time.

risetime(x,t);

Figure Rise Time Plot contains an axes object. The axes object with xlabel Time (seconds), ylabel Level (Volts) contains 12 objects of type patch, line. One or more of the lines displays its values using only markers These objects represent rise time, signal, upper cross, lower cross, upper boundary, upper state, lower boundary, upper reference, lower reference, lower state.

Open Live Script

Determine the rise time, reference-level instants, and reference levels in a 2.3 V clock waveform sampled at 4 MHz.

Load the 2.3 V clock waveform along with the sampling instants.

load("transitionex.mat","x","t")

Determine the rise time, reference-level instants, and reference levels.

[R,lt,ut,ll,ul] = risetime(x,t);

Plot the waveform with the lower- and upper-reference levels and reference-level instants. Show that the rise time is the difference between the upper- and lower-reference level instants.

plot(t,x)
xlabel("Seconds")
ylabel("Volts")

hold on
plot([lt ut],[ll ul],"o")
hold off

Figure contains an axes object. The axes object with xlabel Seconds, ylabel Volts contains 2 objects of type line. One or more of the lines displays its values using only markers

fprintf('Rise time is %g seconds.',ut-lt)
Rise time is 1.78e-07 seconds.
Open Live Script

Generate two signals that represent bilevel waveforms. The signals are sampled at 50 Hz for 20 seconds. For the first signal, the transition occurs 13 seconds after the start of the measurement. For the second signal, the transition occurs 5 seconds after the start of the measurement. The signals have different amplitudes and are embedded in white Gaussian noise of different variances. Plot the signals.

tt = linspace(0,20,1001)';
e1 = 1.4*tanh(tt-13)+randn(size(tt))/3;
e2 = tanh(3*(tt-5))+randn(size(tt))/5;

plot(tt,e1,tt,e2)

Figure contains an axes object. The axes object contains 2 objects of type line.

Align the signals so their transition times coincide. Correlation-based methods cannot align this type of signals adequately.

[y1,y2,D] = alignsignals(e1,e2);

plot(y1)
hold on
plot(y2)
hold off

Figure contains an axes object. The axes object contains 2 objects of type line.

Use risetime to align the signals. For each signal, find the transition time as the average of the instant at which the signal crosses the lower reference level and the instant at which it crosses the upper reference level. Plot the aligned waveforms.

[~,l1,u1] = risetime(e1,tt);
[~,l2,u2] = risetime(e2,tt);

t1 = tt-(l1+u1)/2;
t2 = tt-(l2+u2)/2;

plot(t1,e1,t2,e2)

Figure contains an axes object. The axes object contains 2 objects of type line.

Open Live Script

Determine the rise time in a 2.3 V clock waveform sampled at 4 MHz. Compute the rise time using the 20% and 80% reference levels.

Load the 2.3 V clock data with sampling instants. Compute the sample rate as the inverse of the time difference between consecutive samples. Determine the rise time using the 20% and 80% reference levels. Plot the annotated waveform.

load("transitionex.mat","x","t")

fs = 1/(t(2)-t(1));

risetime(x,fs,PercentReferenceLevels=[20 80])

Figure Rise Time Plot contains an axes object. The axes object with xlabel Time (seconds), ylabel Level (Volts) contains 12 objects of type patch, line. One or more of the lines displays its values using only markers These objects represent rise time, signal, upper cross, lower cross, upper boundary, upper state, lower boundary, upper reference, lower reference, lower state.

ans = 
1.3350e-07

Input Arguments

collapse all

Bilevel waveform, specified as a real-valued vector.

Sample rate, specified as a positive real scalar in hertz.

Sample instants, specified as a vector. The length of t must equal the length of the bilevel waveform x.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: StateLevels=[0 0.8],Tolerance=10,PercentReferenceLevels=[20 50] specifies that the low and high levels are 0 ± 10% and 0.8 ± 10%, respectively, and that a transition occurs when the signal crosses from 0.8 × 0.2 to 0.8 × 0.5.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: "StateLevels",[0 0.8],"Tolerance",10,"PercentReferenceLevels",[20 50]

Reference levels as a percentage of the waveform amplitude, specified as a two-element positive row vector. The elements of the row vector correspond to the lower and upper percent reference levels. The high state level is defined to be 100 percent and the low state level is defined to be 0 percent. See Percent Reference Levels for more details.

Low and high state levels, specified as a two-element row vector. The first and second elements of the vector correspond to the low and high state levels.

Lower- and upper-state boundaries, specified as a real positive scalar as a percentage value. For more information, see State-Level Tolerances.

Output Arguments

collapse all

Duration of positive-going transition, returned as a vector. If you specify the sample rate Fs or the sample instants t, the rise times are in seconds. If you do not specify a sample rate or sample instants, the rise times are in samples.

Lower reference-level crossing instants, returned as a vector. The vector lt contains the time instants when the positive-going transition crosses the lower reference level. By default, the lower reference level is the 10% reference level. You can change the default reference levels by specifying PercentReferenceLevels.

Upper reference-level crossing instants, returned as a vector. The vector ut contains the time instants when the positive-going transition crosses the upper reference level. By default, the upper reference level is the 90% reference level. You can change the default reference levels by specifying PercentReferenceLevels.

Lower reference level in waveform amplitude units, returned as a real numeric scalar. ll is a vector containing the waveform values corresponding to the lower reference level in each positive-going transition. By default, the lower reference-level is the 10% reference level. You can change the default reference-levels by specifying PercentReferenceLevels.

Upper reference level in waveform amplitude units, returned as a real numeric scalar. ul is a vector containing the waveform values corresponding to the upper reference level in each positive-going transition. By default, the upper reference level is the 90% reference level. You can change the default reference levels by specifying PercentReferenceLevels.

More About

collapse all

Positive-Going Transition

A positive-going transition in a bilevel waveform is a transition from the low-state level to the high-state level. A positive-polarity (positive-going) pulse has a terminating state more positive than the originating state. If the waveform is differentiable in the neighborhood of the transition, an equivalent definition is a transition with a positive first derivative. This figure shows a positive-going transition.

Figure Rise Time Plot contains an axes object. The axes object with xlabel Seconds, ylabel Volts contains 5 objects of type line,text. One or more of the lines displays its values using only markers These objects represent positive-going transition, signal.

The amplitude values of the waveform do not appear because a positive-going transition does not depend on the actual waveform values. A positive-going transition is defined by the direction of the transition.

Percent Reference Levels

If S1 is the low state, S2 is the high state, and U is the upper-percent reference level, the waveform value corresponding to the upper percent reference level is

S1+U100(S2−S1).

If L is the lower-percent reference level, the waveform value corresponding to the lower percent reference level is

S1+L100(S2−S1).

State-Level Tolerances

You can specify lower- and upper-state boundaries for each state level. Define the boundaries as the state level plus or minus a scalar multiple of the difference between the high state and the low state. To provide a useful tolerance region, specify the scalar as a small number such as 2/100 or 3/100. In general, the α% region for the low state is defined as

S1±α100(S2-S1),

where S1 is the low-state level and S2 is the high-state level. Replace the first term in the equation with S2 to obtain the α% tolerance region for the high state.

This figure shows lower and upper 5% state boundaries (tolerance regions) for a positive-polarity bi-level waveform. The thick dashed lines indicate the estimated state levels.

0000.png

References

[1] IEEE® Standard on Transitions, Pulses, and Related Waveforms, IEEE Standard 181, 2003, pp. 15–17.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2012a

See Also

| |