statelevels
State-level estimation for bilevel waveform with histogram method
Syntax
Description
levels = statelevels(x)x using the histogram method. For more information, see
Algorithms.
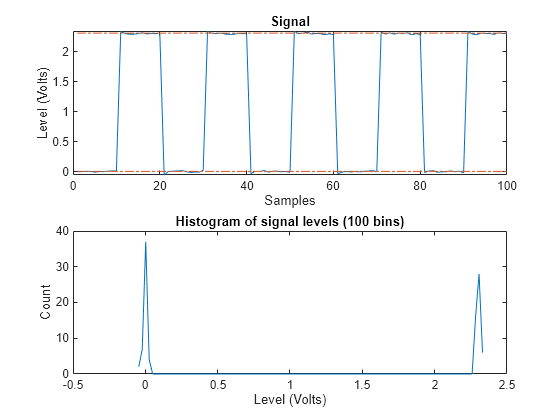
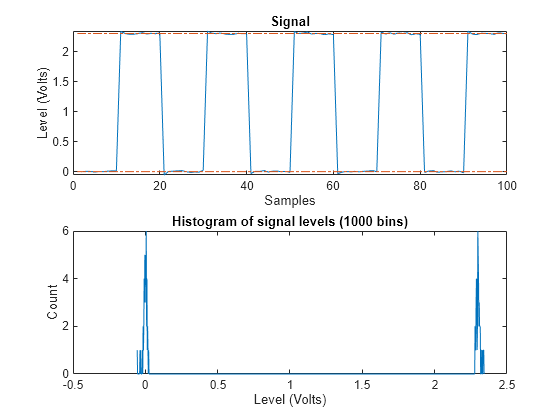
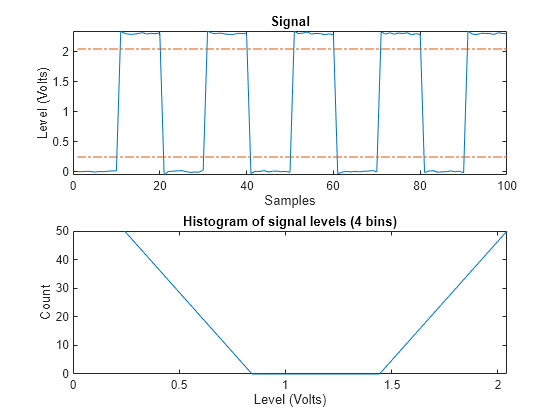
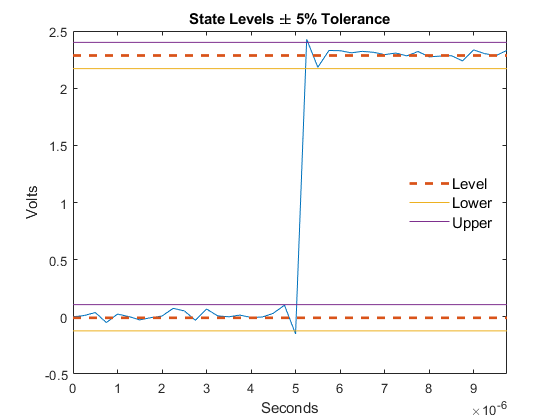
statelevels(___) displays a plot of the
signal and the corresponding histogram.
Examples
Input Arguments
Output Arguments
More About
Algorithms
statelevels uses the histogram method to estimate the states of a bilevel
waveform. The histogram method is described in [1]. The steps of this
method are:
Determine the maximum and minimum amplitudes and amplitude range of the data.
For the specified number of histogram bins, determine the bin width, which is the ratio of the amplitude range to the number of bins.
Sort the data values into the histogram bins.
Identify the lowest-indexed histogram bin, , and highest-indexed histogram bin, ihigh, with nonzero counts.
Divide the histogram into two subhistograms:
The indices of the lower histogram bins are .
The indices of the upper histogram bins are .
Compute the state levels by determining the mode or mean of the lower and upper histograms.
References
[1] IEEE® Standard on Transitions, Pulses, and Related Waveforms, IEEE Standard 181, 2003, pp. 15–17.
Extended Capabilities
Version History
Introduced in R2012a
See Also
midcross | overshoot | risetime | undershoot