离散傅里叶变换
离散傅里叶变换(即 DFT)是数字信号处理的首要工具。该产品的基础是快速傅里叶变换 (FFT),这是一种可减少执行时间的 DFT 计算方法。许多工具箱函数(包括 Z 域频率响应、频谱和倒频谱分析,以及一些滤波器设计和实现函数)都支持 FFT。
MATLAB® 环境提供 fft 和 ifft 函数,分别用于计算离散傅里叶变换及其逆变换。对于输入序列 x 及其变换版本 X(围绕单位圆的等间距频率的离散时间傅里叶变换),这两个函数实现以下关系
和
在这些方程中,序列下标从 1 而不是 0 开始,因为采用 MATLAB 向量索引方案,并且
注意 MATLAB 约定是对 fft 函数使用负 j。这是工程约定;物理和纯数学通常使用正 j。
使用单个输入参量 x 的 fft 计算输入向量或矩阵的 DFT。如果 x 是向量,fft 计算向量的 DFT;如果 x 是矩形数组,fft 计算每个数组列的 DFT。
例如,创建时间向量和信号:
t = 0:1/100:10-1/100; % Time vector x = sin(2*pi*15*t) + sin(2*pi*40*t); % Signal
计算信号的 DFT 以及变换后的序列的幅值和相位。通过将小幅值变换值设置为零来减少计算相位时的舍入误差。
y = fft(x); % Compute DFT of x m = abs(y); % Magnitude y(m<1e-6) = 0; p = unwrap(angle(y)); % Phase
要以度为单位绘制幅值和相位,请键入以下命令:
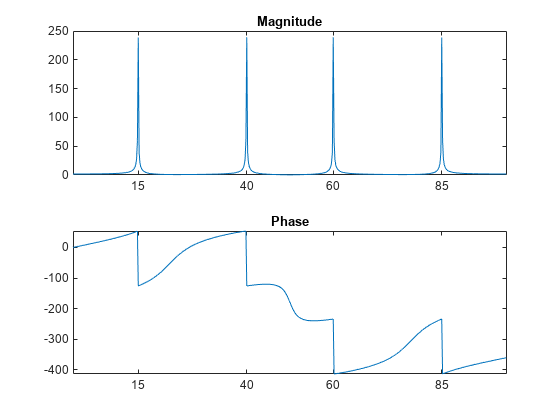
f = (0:length(y)-1)*100/length(y); % Frequency vector subplot(2,1,1) plot(f,m) title('Magnitude') ax = gca; ax.XTick = [15 40 60 85]; subplot(2,1,2) plot(f,p*180/pi) title('Phase') ax = gca; ax.XTick = [15 40 60 85];

fft 的第二个参量指定变换的点数 n,表示 DFT 的长度:
n = 512; y = fft(x,n); m = abs(y); p = unwrap(angle(y)); f = (0:length(y)-1)*100/length(y); subplot(2,1,1) plot(f,m) title('Magnitude') ax = gca; ax.XTick = [15 40 60 85]; subplot(2,1,2) plot(f,p*180/pi) title('Phase') ax = gca; ax.XTick = [15 40 60 85];
在本例中,如果输入序列比 n 短,fft 会用零填充输入序列,如果输入序列比 n 长,则会截断序列。如果未指定 n,则默认为输入序列的长度。fft 的执行时间取决于其执行的 DFT 的长度 n;有关该算法的详细信息,请参阅 fft 参考页。
注意 得到的 FFT 振幅是 A*n/2,其中 A 是原始振幅,n 是 FFT 点数。仅当 FFT 点的数量大于或等于数据样本的数量时,上述情形才成立。如果 FFT 点数小于数据样本数,则 FFT 振幅比原始振幅低上述量。
离散傅里叶逆变换函数 ifft 也接受输入序列以及可选的变换所需点数。尝试以下示例;原始序列 x 和重新构造的序列是相同的(在舍入误差内)。
t = 0:1/255:1; x = sin(2*pi*120*t); y = real(ifft(fft(x))); figure plot(t,x-y)
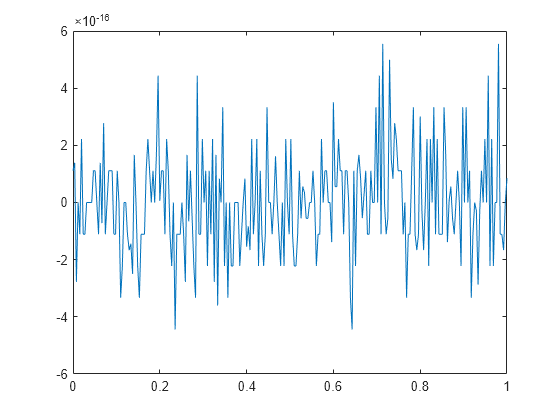
该工具箱还包括二维 FFT 及其逆变换的函数,即 fft2 和 ifft2。这些函数对于二维信号或图像处理非常有用。格兹尔函数是计算 DFT 的另一种算法,它也包含在工具箱中。此函数可高效计算长信号中一部分的 DFT。
有时可以方便地重新排列 fft 或 fft2 函数的输出,使零频率分量位于序列的中心。函数 fftshift 将零频率分量移至向量或矩阵的中心。