振动信号的阶次分析

此示例说明如何使用阶次分析来分析振动信号。阶次分析用于量化转速随时间变化的旋转机械中的噪声或振动。阶次指的是参考转速的某个倍数的频率。例如，频率等于发动机旋转频率两倍的振动信号对应的是阶次 2，同样，频率等于发动机旋转频率 0.5 倍的振动信号对应的是阶次 0.5。此示例通过确定大振幅的阶次来调查直升机舱中不必要的振动的来源。

简介

此示例分析在主发动机加速和减速过程中，来自直升机舱中加速度计的仿真振动数据。直升机有几个旋转部件，包括发动机、变速箱、主旋翼和尾旋翼。每个部件以相对于主发动机的已知固定速率旋转，每个部件都可能是不必要振动的诱发因素。可以将主要振动部件的频率与发动机的转速相关联，以研究高振幅振动的来源。此示例中的直升机在主旋翼和尾旋翼上都有四个叶片。当振动由旋翼叶片生成时，直升机旋翼振动的重要分量可能是旋翼旋转频率的整数倍。

此示例中的信号是时间依赖电压 vib，采样率 fs 等于 500 Hz。数据包括涡轮发动机的角速度 rpm 和时刻的向量 t。每个旋翼的转速与发动机转速之比存储在变量 mainRotorEngineRatio 和 tailRotorEngineRatio 中。

发动机速度信号通常由一系列转速表脉冲组成。tachorpm 可用于从转速表脉冲信号中提取 RPM 信号。tachorpm 自动识别双水平转速表波形的脉冲位置，并计算脉冲之间的间隔以估计转速。在此示例中，发动机速度信号包含转速 rpm，因此不需要转换。

绘制发动机速度和振动数据对时间的图：

load helidata
vib = vib - mean(vib);  % Remove the DC component 

subplot(2,1,1) 
plot(t,rpm)             % Plot the engine rotational speed
xlabel('Time (s)') 
ylabel('Engine Speed (RPM)')
title('Engine speed')

subplot(2,1,2) 
plot(t,vib)             % Plot the vibration signal 
xlabel('Time (s)') 
ylabel('Voltage (mV)')
title('Accelerometer Vibration Data')

发动机转速在加速过程中增加，在减速过程中降低。振幅随着转速变化。这种类型的 RPM 曲线通常用于旋转机械振动分析。

使用 RPM-频率图可视化数据

可以使用函数 rpmfreqmap 在频域中可视化振动信号。此函数计算信号的短时傅里叶变换，并生成 RPM-频率图。当省略输出参数时，rpmfreqmap 在交互式绘图窗口中显示图。

生成并可视化振动数据的 RPM-频率图。

rpmfreqmap(vib,fs,rpm)

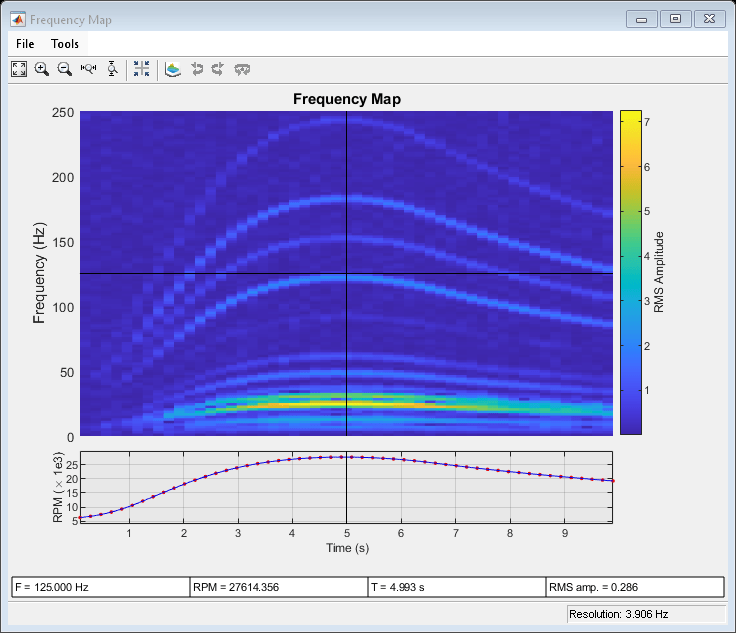
由 rpmfreqmap 生成的交互式图窗窗口包含 RPM-频率图、对应于该图的 RPM 对时间的曲线图，以及可用于量化振动分量的几个数值指示符。默认情况下，图的振幅是均方根 (RMS) 振幅。可使用可选参数指定其他振幅选项，包括峰值振幅和功率。瀑布图菜单按钮生成一个三维视图：

RPM-频率图中的许多轨迹具有随发动机速度增加和减少的频率。这表明轨迹是发动机旋转频率的阶次。RPM 峰值附近有高振幅分量，频率在 20 至 30 Hz 之间。可以将十字准线放在图上的此位置，以在 RPM 曲线图下方的指标框中查看频率、RPM 值、时间以及图振幅。

默认情况下，rpmfreqmap 通过将采样率除以 128 来计算分辨率。分辨率显示在图窗的右下角，在本例中等于 3.906 Hz。默认情况下使用 Hann 窗，但也可以使用其他几种窗口。

将较小的分辨率值传递给 rpmfreqmap 可更好地解析某些频率分量。例如，低频分量在 RPM 峰值时没有分离。在低 RPM 值下，高振幅轨迹混合在一起。

生成分辨率为 1 Hz 的 RPM-频率图可解析这些分量。

rpmfreqmap(vib,fs,rpm,1)

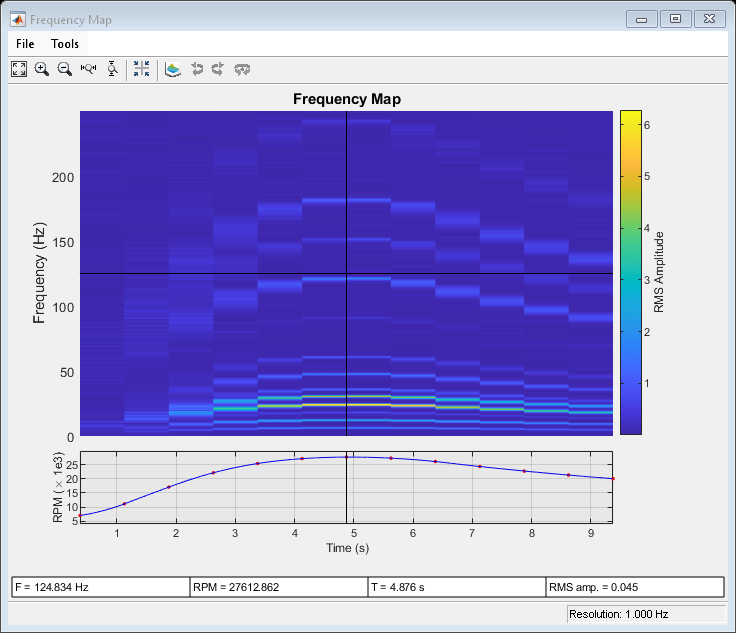
低频分量现在可以在 RPM 峰值处解析，但在转速变化更快时，会出现明显的涂抹现象。随着发动机速度的增加或减少，振动阶次在每个时间窗内更改频率，产生更宽的频谱轨迹。由于需要更长的时间窗，这种涂抹效应对于更精细的分辨率来说更加明显。在本例中，提高频谱分辨率会导致加速和减速阶段的涂抹伪影增加。可以生成阶次图来避免这种权衡。

使用 RPM-阶次图可视化数据

函数 rpmordermap 为阶次分析生成阶次对 RPM 的频谱图。该方法通过以恒定相位增量对信号进行重采样来消除涂抹伪影，为每个阶次产生一个平稳正弦波。使用短时傅里叶变换来分析重采样的信号。由于每个阶次均为参考转速的固定倍数，对于每个阶次，阶次图包含其对 RPM 的一条直线轨迹图。

函数 rpmordermap 接受与 rpmfreqmap 相同的参数，并且在不带输出参数调用时还会生成交互式绘图窗口。分辨率参数现在以阶次而不是 Hz 指定，并且图的频谱轴现在是阶次而不是频率。默认情况下，该函数使用平顶窗口。

使用 rpmordermap 可视化直升机数据的阶次图。指定以 0.005 阶次为单位的阶次分辨率。

rpmordermap(vib,fs,rpm,0.005)

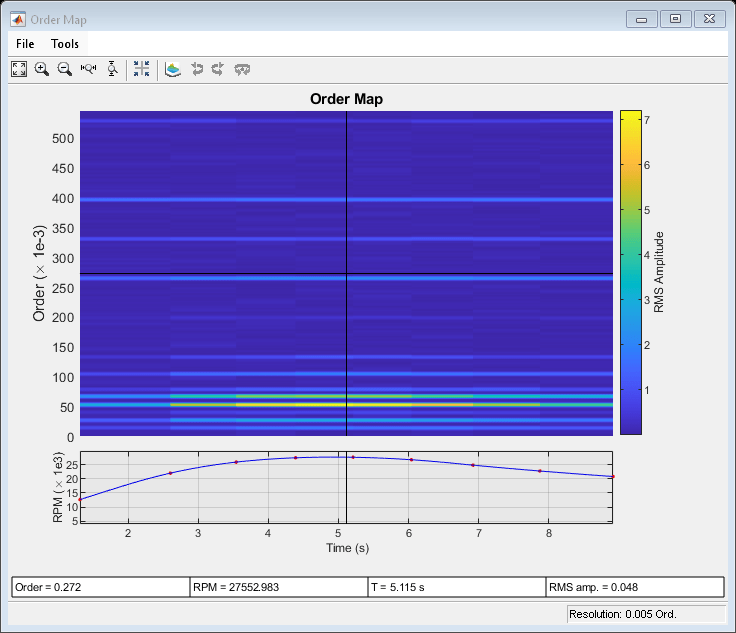
对于每个阶次，该图包含一条直线轨迹，表明振动出现在发动机转速的固定倍数处。阶次图可以更轻松地展示每个频谱分量与发动机速度的关系。与 RPM-频率图相比，涂抹伪影显著减少。

使用平均阶次谱确定峰值阶次

接下来，确定阶次图的峰值位置。寻找主旋翼和尾旋翼阶次的整数倍的阶次，这些旋翼会在这些位置产生振动。函数 rpmordermap 返回图以及对应的阶次和 RPM 值作为输出。分析数据以确定直升机舱内高振幅振动的对应阶次。

计算并返回数据的阶次图。

[map,mapOrder,mapRPM,mapTime] = rpmordermap(vib,fs,rpm,0.005);

接下来，使用 orderspectrum 计算并绘制 map 的平均频谱。该函数接受 rpmordermap 生成的阶次图作为输入，并随时间对其求平均值。

figure
orderspectrum(map,mapOrder)

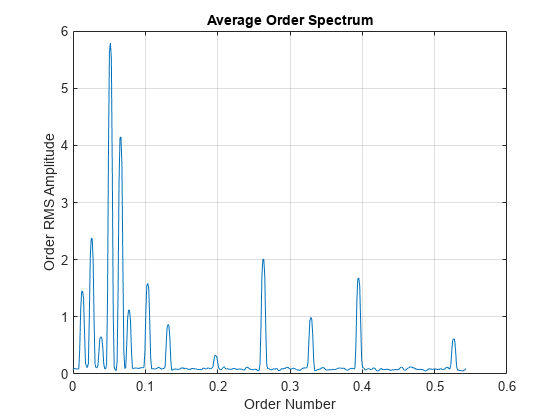
返回平均频谱，并调用 findpeaks 以返回两个最高峰值的位置。

[spec,specOrder] = orderspectrum(map,mapOrder);          
[~,peakOrders] = findpeaks(spec,specOrder,'SortStr','descend','NPeaks',2);
peakOrders = round(peakOrders,3)

peakOrders = 2×1

    0.0520
    0.0660

在图中大约 0.05 阶次处可以看到两个间隔很近的主峰。阶次小于 1，因为振动频率低于发动机转速。

分析峰值阶次随时间的变化

接下来，使用 ordertrack 求峰值阶次的幅值随时间的变化。使用 map 作为输入，通过不带输出参数调用 ordertrack 来绘制两个峰值阶次的振幅。

ordertrack(map,mapOrder,mapRPM,mapTime,peakOrders)

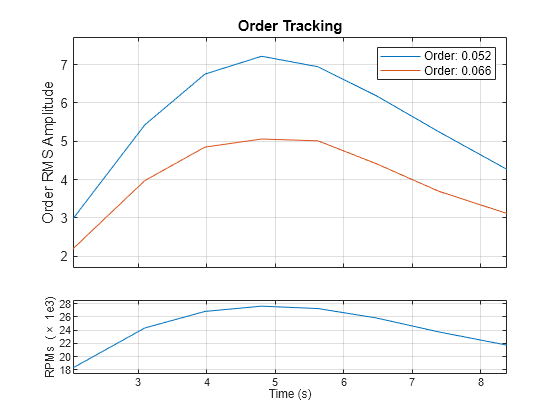
随着发动机转速的增加，两个阶次的振幅都会增加。尽管在这种情况下可以轻松分离阶次，不过 ordertrack 还可以在存在多个 RPM 信号时分离交叉阶次。

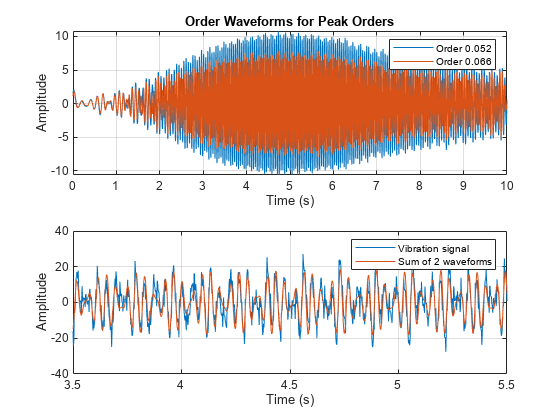
接下来，使用 orderwaveform 提取每个峰值阶次的时域阶次波形。阶次波形可以直接与原始振动信号进行比较，并作为音频播放。orderwaveform 使用 Vold-Kalman 滤波器提取指定阶次的波形。将两个峰值阶次波形之和与原始信号进行比较。

orderWaveforms = orderwaveform(vib,fs,rpm,peakOrders);
helperPlotOrderWaveforms(t,orderWaveforms,vib)

减少机舱振动

为了确定机舱振动的来源，将每个峰值的阶次与直升机每个旋翼的阶次进行比较。每个旋翼的阶次等于旋翼转速与发动机转速的固定比率。

mainRotorOrder = mainRotorEngineRatio; 
tailRotorOrder = tailRotorEngineRatio;

ratioMain = peakOrders/mainRotorOrder

ratioMain = 2×1

    4.0310
    5.1163

ratioTail = peakOrders/tailRotorOrder

ratioTail = 2×1

    0.7904
    1.0032

最高峰值位于主旋翼速度的四阶次处，因此最大振幅分量的频率是主旋翼频率的四倍。主旋翼有四个叶片，很可能是这种振动的来源，因为对于每个旋翼有 N 个叶片的直升机来说，以旋翼转速的 N 倍振动是很常见的。同样，第二大分量位于尾旋翼速度的一阶次处，表明振动可能源于尾旋翼。由于旋翼的速度不是整数倍数关系，因此第二大峰值相对于主旋翼速度的阶次不是整数。

在对主旋翼和尾旋翼进行轨迹和平衡调整后，采集新数据集。加载新数据集并比较调整前后的阶次频谱。

load helidataAfter
vib = vib - mean(vib);             % Remove the DC component 
[mapAfter,mapOrderAfter] = rpmordermap(vib,fs,rpm,0.005);
figure
hold on  
orderspectrum(map,mapOrder)
orderspectrum(mapAfter,mapOrderAfter)
legend('Before Adjustment','After Adjustment')

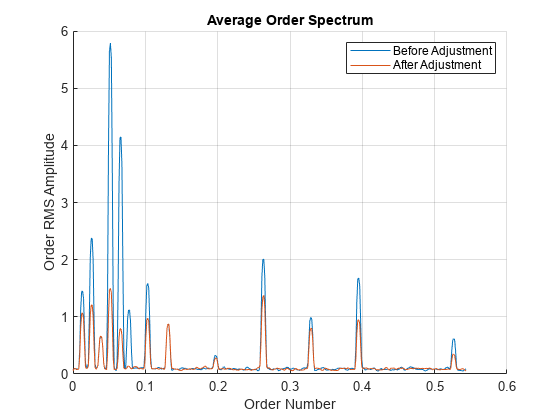
主峰的振幅现在大幅降低。

总结

此示例使用阶次分析来确定直升机的主旋翼和尾旋翼是否为机舱内高振幅振动的潜在来源。首先，使用了 rpmfreqmap 和 rpmordermap 对阶次进行可视化。RPM-阶次图在整个 RPM 范围内实现了阶次分离，且消除了在 RPM-频率图中出现的涂抹伪影。rpmordermap 最适合可视化在发动机加速和减速期间低 RPM 时的振动分量。

接下来，该示例使用 orderspectrum 确定峰值阶次，使用 ordertrack 可视化峰值阶次的振幅随时间的变化情况，使用 orderwaveform 提取峰值阶次的时域波形。最大的振幅振动分量出现在主旋翼旋转频率的四倍处，表明主旋翼叶片不平衡。第二大分量出现在尾旋翼的旋转频率处。调整旋翼后，振动程度得以降低。

参考资料

Brandt, Anders.Noise and Vibration Analysis:Signal Analysis and Experimental Procedures.Chichester, UK:John Wiley and Sons, 2011.

另请参阅

orderspectrum | ordertrack | orderwaveform | rpmfreqmap | rpmordermap