ordertrack
Track and extract order magnitudes from vibration signal
Syntax
Description
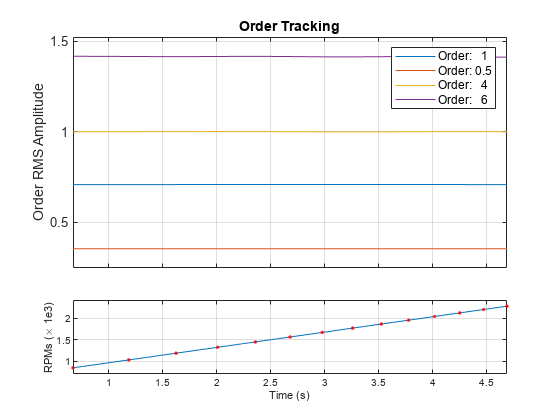
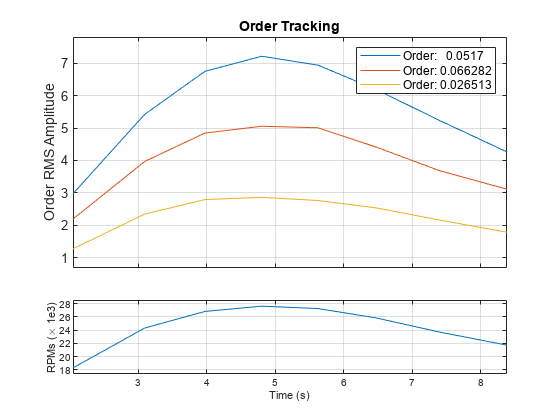
mag = ordertrack(x,fs,rpm,orderlist)mag, that contains time-dependent root-mean-square
(RMS) amplitude estimates of a specified set of orders, orderlist,
present in input signal x. x is
measured at a set rpm of rotational speeds expressed
in revolutions per minute. fs is the measurement
sample rate in Hz.
[___] = ordertrack(___,
specifies further options using Name,Value)Name,Value pairs. Some of
the options apply only to the Vold-Kalman tracking procedure.
ordertrack(___) with no output
arguments plots in the current figure the time-dependent orders and
RPM values.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Brandt, Anders. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures. Chichester, UK: John Wiley & Sons, 2011.
[2] Feldbauer, Christian, and Robert Höldrich. "Realization of a Vold-Kalman Tracking Filter — A Least Squares Problem." Proceedings of the COST G-6 Conference on Digital Audio Effects (DAFX-00). Verona, Italy, December 7–9, 2000.
[3] Vold, Håvard, and Jan Leuridan. "High Resolution Order Tracking at Extreme Slew Rates Using Kalman Tracking Filters." Shock and Vibration. Vol. 2, 1995, pp. 507–515.
[4] Tůma, Jiří. “Algorithms for the Vold-Kalman Multiorder Tracking Filter.” Proceedings of the 14th International Carpathian Control Conference (ICCC), 2013, pp. 388–94. https://doi.org/10.1109/CarpathianCC.2013.6560575.
Extended Capabilities
Version History
Introduced in R2016b
See Also
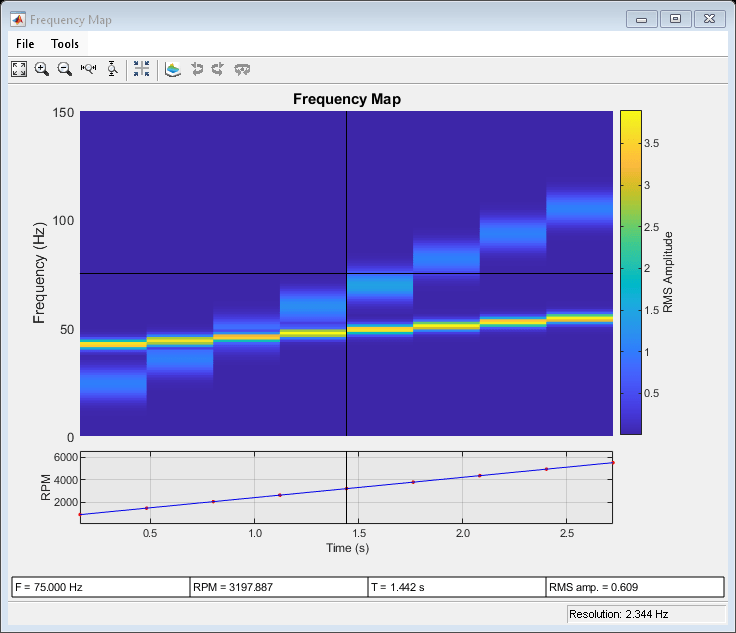
orderspectrum | orderwaveform | rpmfreqmap | rpmordermap | tachorpm