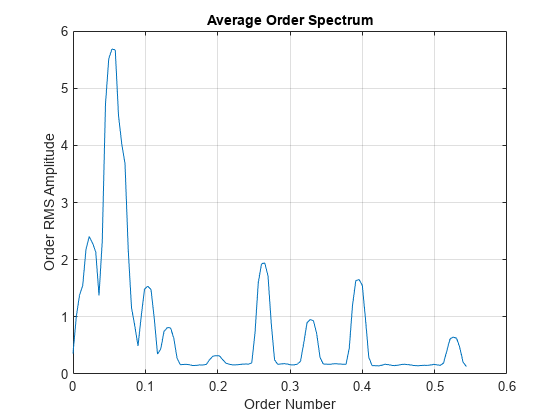
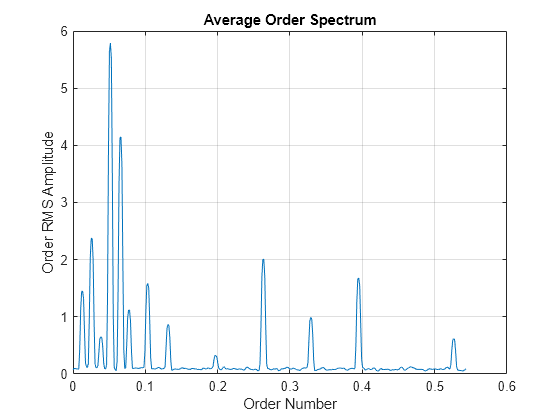
orderspectrum
Average spectrum versus order for vibration signal
Syntax
Description
[ computes
an average order-magnitude spectrum vector starting from an order-RPM
map and a vector of orders. Use spec,order]
= orderspectrum(map,order)rpmordermap to
compute map and order. map must
be linearly scaled. The returned amplitudes are the same as in map.
The returned spectrum is scaled linearly.
orderspectrum(___) with no
output arguments plots the RMS amplitude of the order spectrum, scaled
linearly, on the current figure.
Examples
Input Arguments
Output Arguments
References
[1] Brandt, Anders. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures. Chichester, UK: John Wiley & Sons, 2011.
[2] Vold, Håvard, and Jan Leuridan. “High Resolution Order Tracking at Extreme Slew Rates Using Kalman Tracking Filters.” Shock and Vibration. Vol. 2, 1995, pp. 507–515.
Extended Capabilities
Version History
Introduced in R2016b
See Also
ordertrack | orderwaveform | rpmfreqmap | rpmordermap | tachorpm