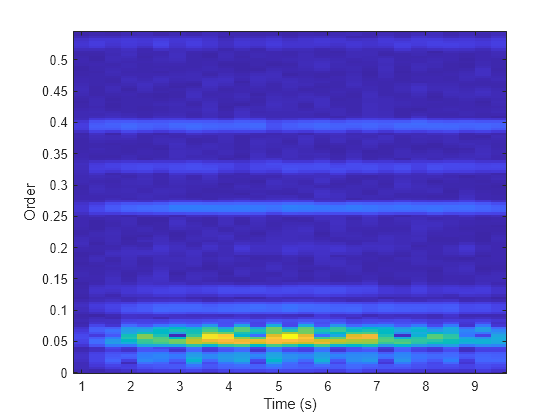
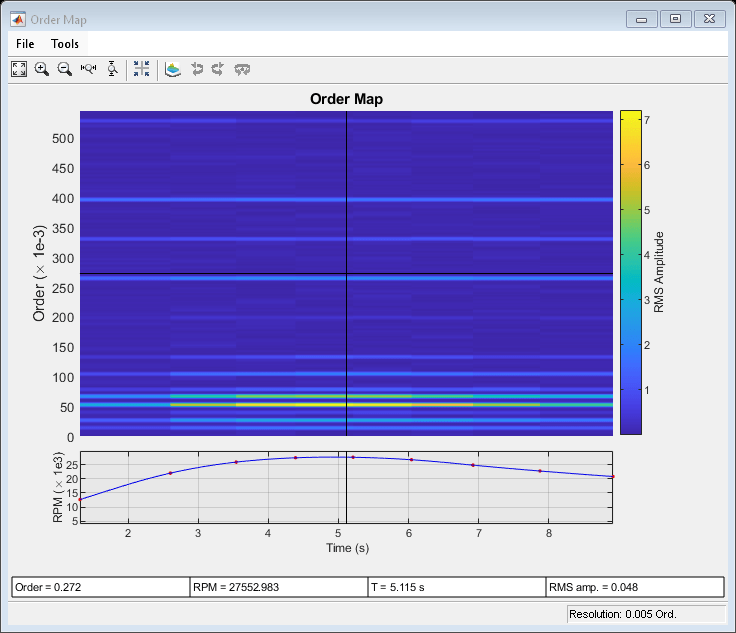
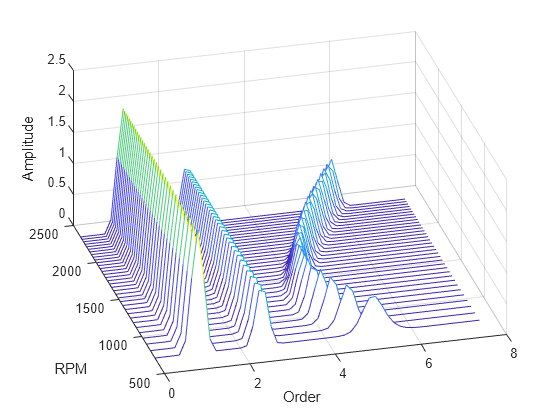
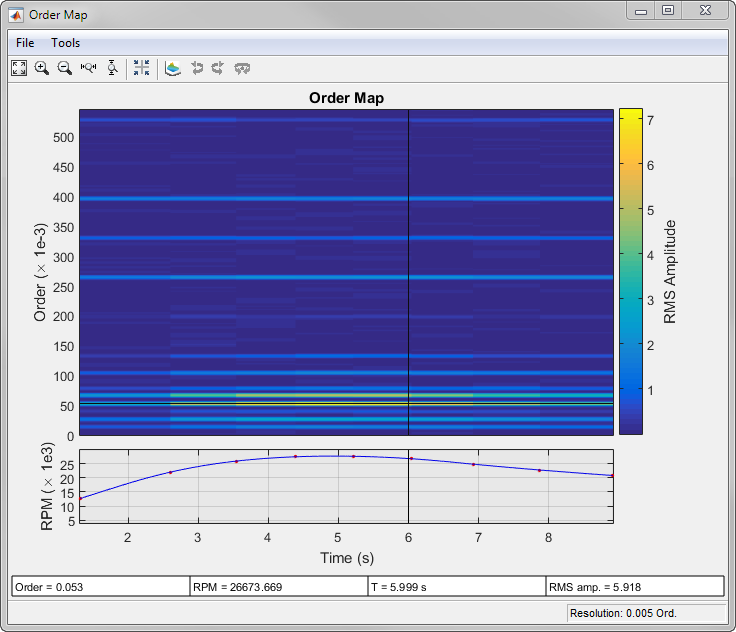
rpmordermap
Order-RPM map for order analysis
Syntax
Description
map = rpmordermap(x,fs,rpm)map, that results from
performing order analysis on the input vector, x. x is
measured at a set rpm of rotational speeds expressed
in revolutions per minute. fs is the measurement
sample rate in Hz. Each column of map contains
root-mean-square (RMS) amplitude estimates of the orders present at
each rpm value. rpmordermap resamples x to
a constant samples-per-cycle rate and uses the short-time Fourier
transform to analyze the spectral content of the resampled signal.
map = rpmordermap(___,Name,Value)Name,Value pairs in addition to
the input arguments in previous syntaxes.
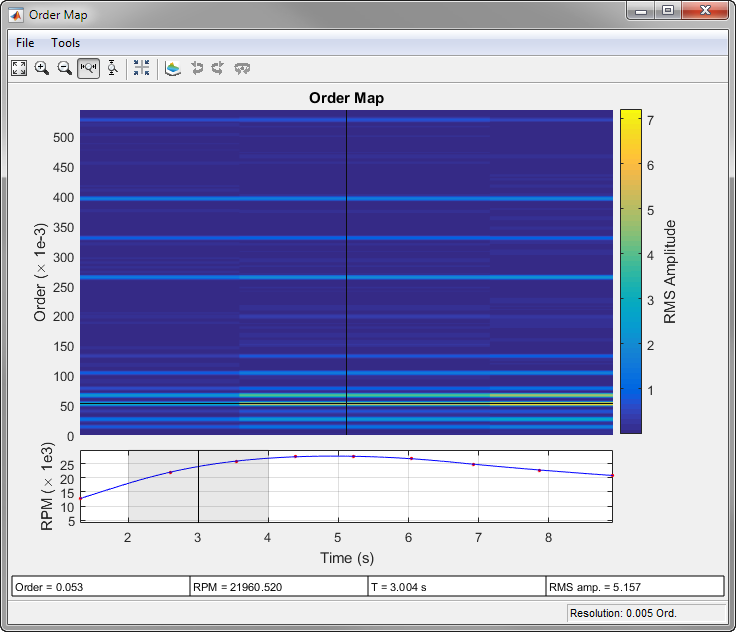
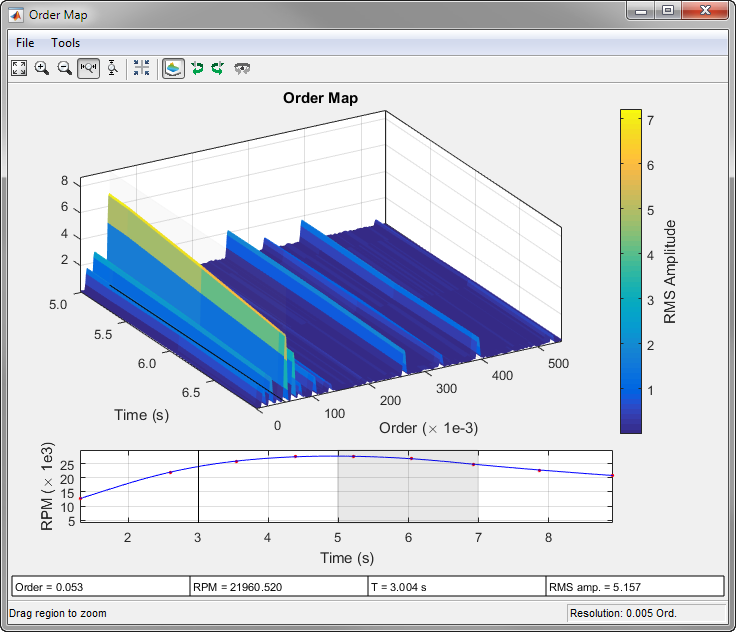
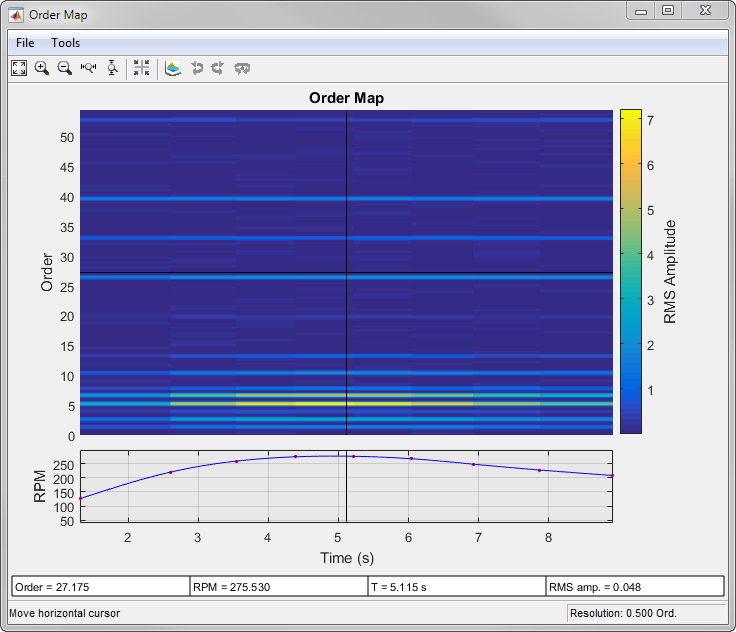
rpmordermap(___) with no output
arguments plots the order map as a function of rotational speed and
time on an interactive figure.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
Order analysis is the study of vibrations in rotating systems that result from the rotation itself. The frequencies of these vibrations are often proportional to the rotational speed. The constants of proportionality are the orders.
The rotational speed is usually measured independently and changes with time under most experimental conditions. Proper analysis of rotation-induced vibrations requires resampling and interpolating the measured signal to achieve a constant number of samples per cycle. Through this process, the signal components whose frequencies are constant multiples of the rotational speed transform into constant tones. The transformation reduces the smearing of spectral components that occurs when frequency changes rapidly with time.
The rpmordermap function performs these
steps:
Uses
cumtrapzto estimate the phase angle as the time integral of the rotational speed:Uses
resampleto upsample and lowpass-filter the signal. This step enables the function to interpolate the signal at nonsampled time points without aliasing of the high-frequency components.rpmordermapupsamples the signal by a factor of 15.Uses
interp1to interpolate the upsampled signal linearly onto a uniform grid in the phase domain. The highest accessible order in a measurement is fixed by the sample rate and the highest rotational speed reached by the system:To capture this highest order accurately, it is necessary to sample the signal at twice Omax at least. For better results,
rpmordermapoversamples by an extra factor of 4. The resulting phase-domain sample rate, fp, isBy default,
rpmordermapis configured to compute order-RPM matrices at a target order resolutionbut you can specify a different value using the
resinput argument.Uses
spectrogramto compute the short-time Fourier transform (STFT) of the interpolated signal. By default, the function divides the signal into L-sample segments and windows each of them with a flat top window. There aresamples of overlap between adjoining segments, where poverlap is specified using the
'OverlapPercent'name-value pair and defaults to 50%. The DFT length is set to L. The resolution is related to the sample rate and segment length throughwhere ENBW, the equivalent noise bandwidth of the window, is computed using
enbw. Adjust the resolution to differentiate closely spaced orders. Smaller r values require larger segment lengths. ENBW itself depends on L, so L must be computed recursively for given r and fp. The resulting L value is usually not an integer, sorpmordermaprounds it usingceil. The actual order resolution may thus differ slightly from the specified target value. If you need to attain a given resolution, make sure that your signal has enough samples.
The red dots in the RPM-vs.-time plot at the bottom of the interactive rpmordermap window
correspond to the right edge of each windowed segment. The blue line
in the plot is the RPM signal drawn as a function of time:
References
[1] Brandt, Anders. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures. Chichester, UK: John Wiley & Sons, 2011.
Extended Capabilities
Version History
Introduced in R2015bSee Also
orderspectrum | ordertrack | orderwaveform | rpmfreqmap | rpmtrack | spectrogram | tachorpm