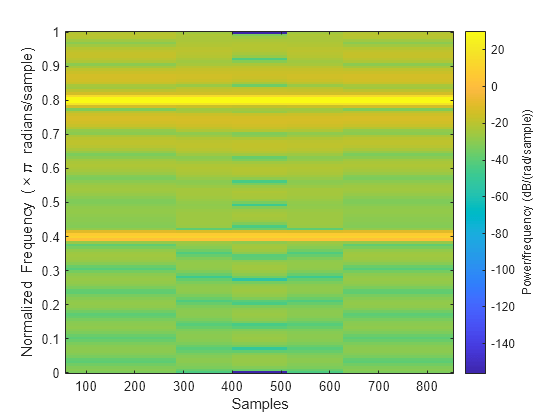
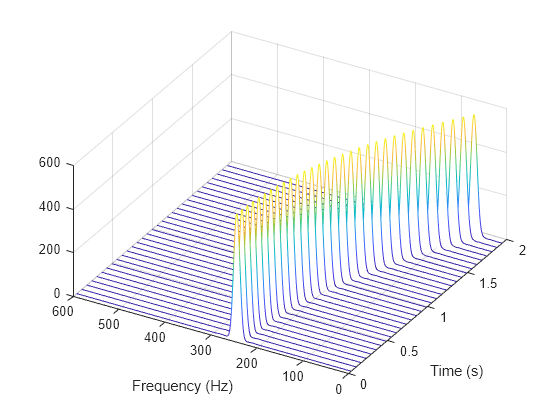
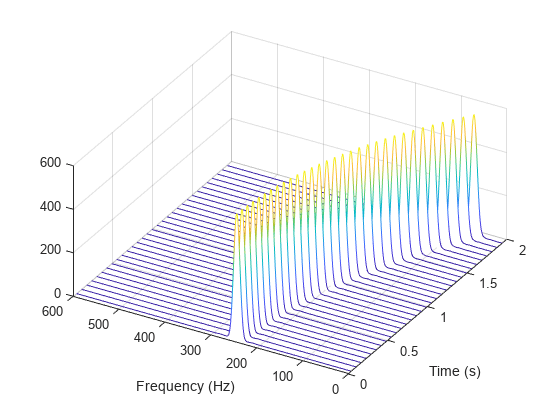
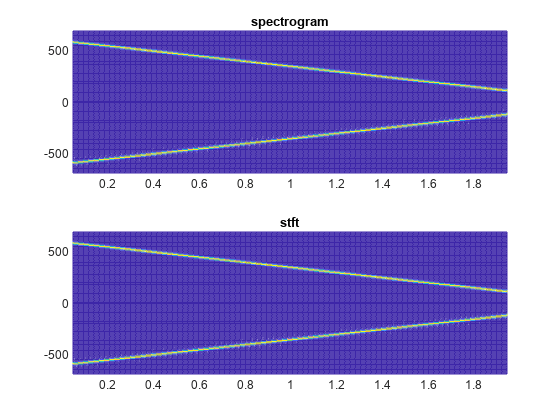
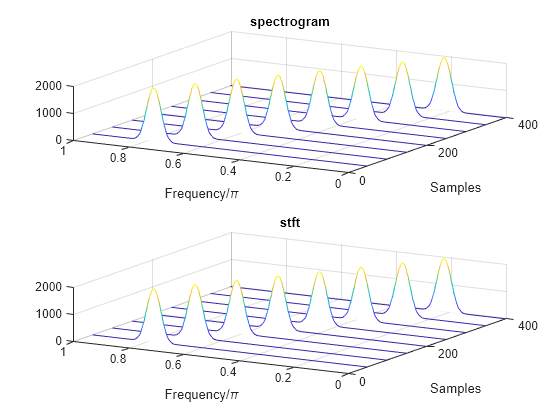
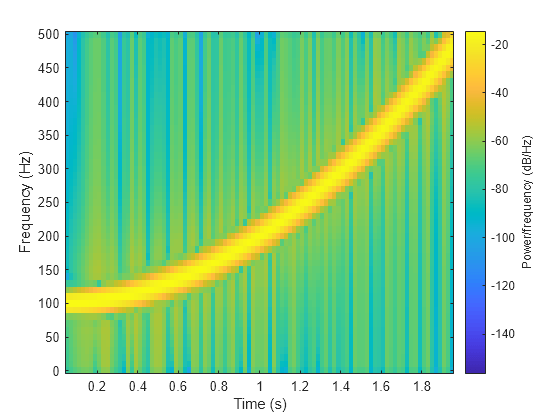
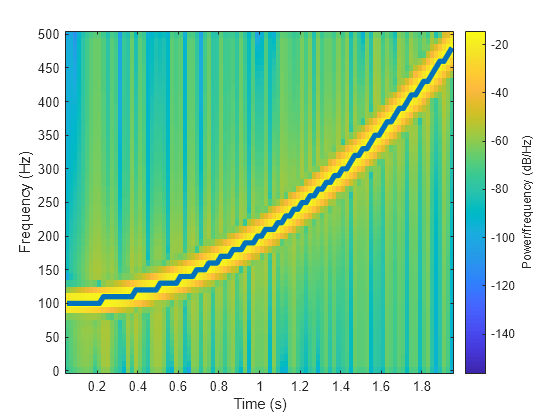
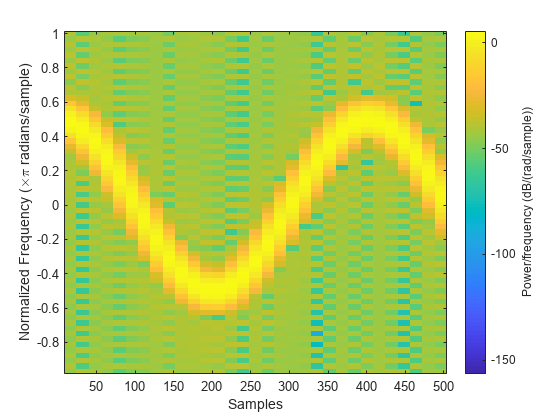
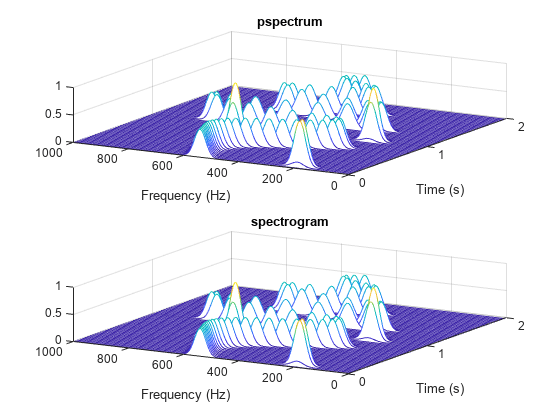
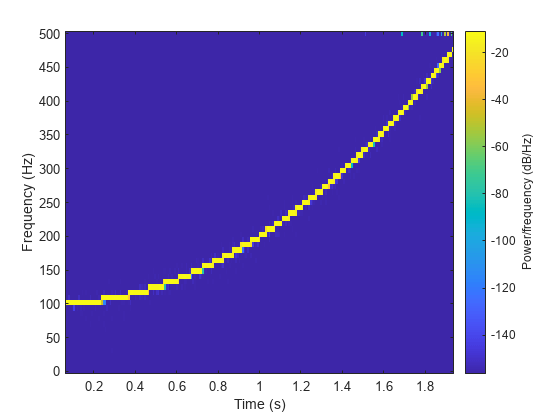
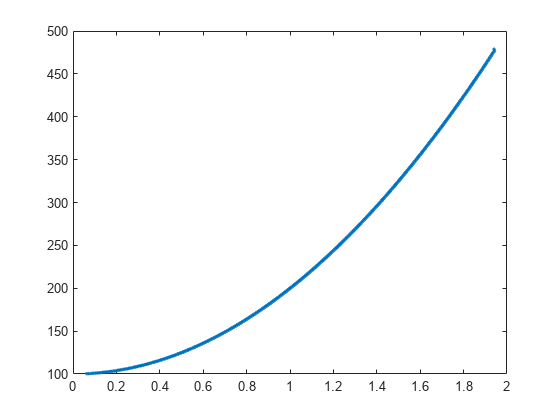
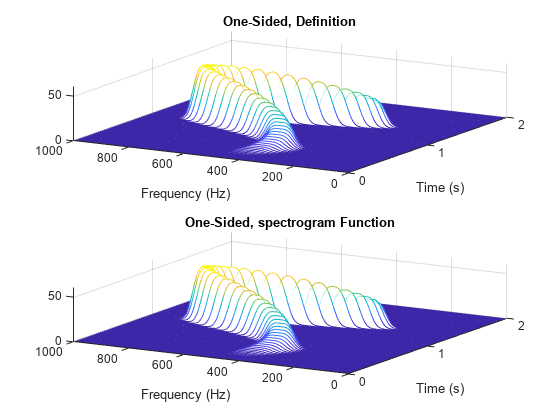
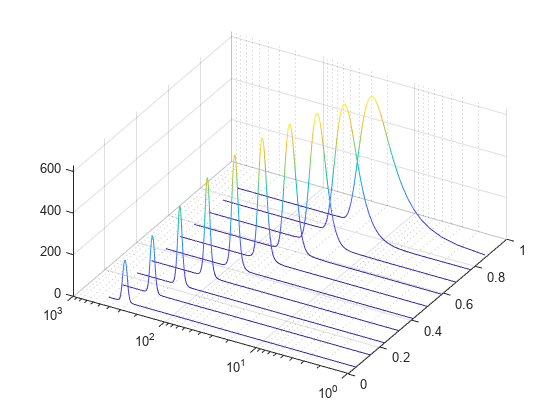
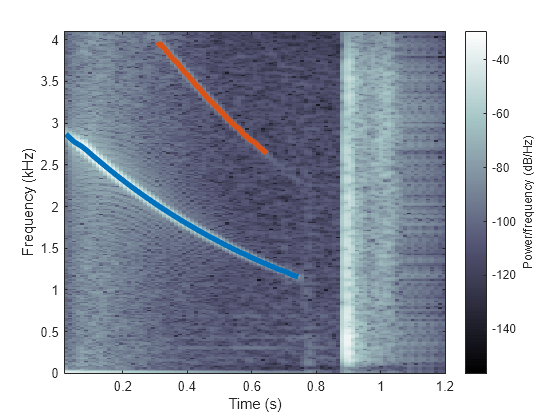
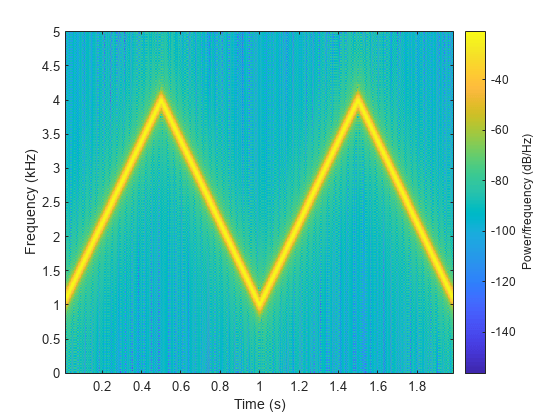
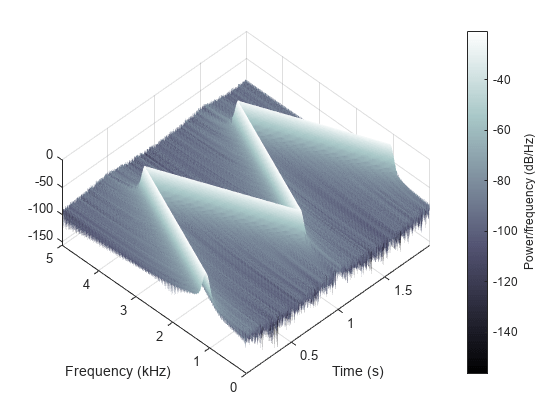
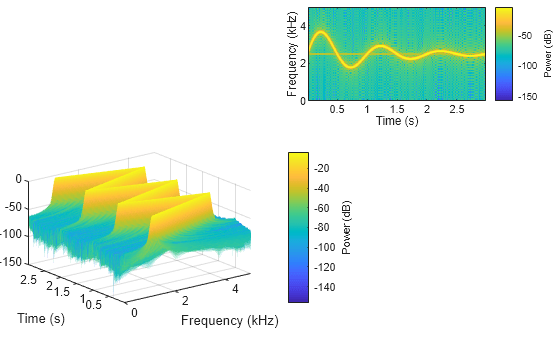
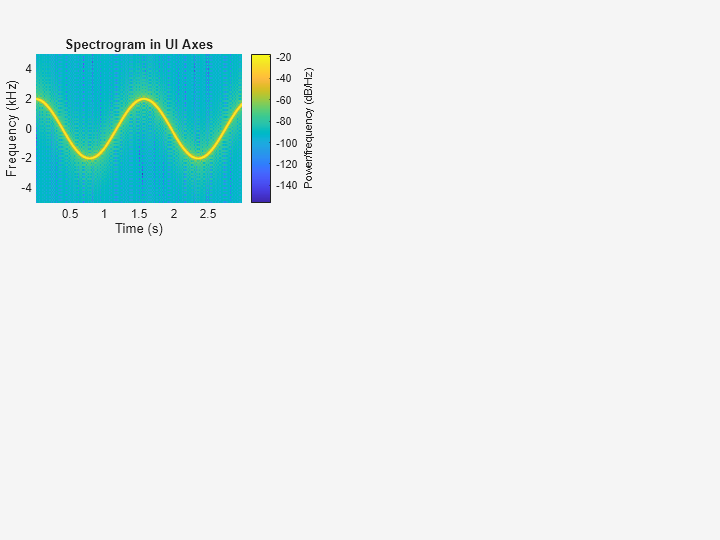
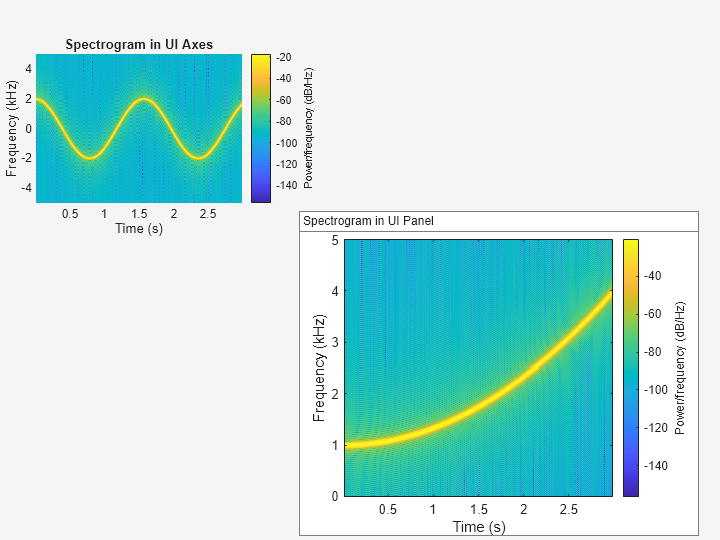
spectrogram

使用短时傅里叶变换的谱图

全页折叠

语法

s = spectrogram(x)

s = spectrogram(x,window)

s = spectrogram(x,window,noverlap)

s = spectrogram(x,window,noverlap,nfft)

[s,w,t] = spectrogram(___)

[s,f,t] = spectrogram(___,fs)

[s,w,t] = spectrogram(x,window,noverlap,w)

[s,f,t] = spectrogram(x,window,noverlap,f,fs)

[___,ps] = spectrogram(___,spectrumtype)

[___] = spectrogram(___,"reassigned")

[___,ps,fc,tc] = spectrogram(___)

[___] = spectrogram(___,freqrange)

[___] = spectrogram(___,Name=Value)

spectrogram(___)

spectrogram(___,freqloc)

说明

s = spectrogram(x) 返回输入信号 x 的短时傅里叶变换 (STFT)。s 的每一列都包含 x 的短期时间局部化频率成分的估计值。s 的幅值平方称为 x 的谱图时频表示 [1]。

示例

s = spectrogram(x,window) 使用 window 将信号分段并执行加窗。

示例

s = spectrogram(x,window,noverlap) 在相邻段之间使用 noverlap 个采样的重叠。

示例

s = spectrogram(x,window,noverlap,nfft) 使用 nfft 个采样来计算离散傅里叶变换。

示例

[s,w,t] = spectrogram(___) 返回归一化频率向量 w 和时刻向量 t，在这些点上计算 STFT。此语法可以包括上述语法中输入参量的任意组合。

示例

[s,f,t] = spectrogram(___,fs) 返回周期性频率向量 f，以采样率 fs 表示。fs 必须为 spectrogram 的第五个输入。要输入采样率并仍使用前面可选参量的默认值，请将这些参量指定为空，即 []。

示例

[s,w,t] = spectrogram(x,window,noverlap,w) 返回在 w 中指定的归一化频率处的 STFT。w 必须包含至少两个元素，否则函数会将其解释为 nfft。

示例

[s,f,t] = spectrogram(x,window,noverlap,f,fs) 返回在 f 中指定的周期性频率处的 STFT。f 必须包含至少两个元素，否则函数会将其解释为 nfft。

示例

[___,ps] = spectrogram(___,spectrumtype) 还返回矩阵 ps，该矩阵与 x 的谱图成正比。

如果您将 spectrumtype 指定为 "psd"，则 ps 的每列包含一个加窗段的功率谱密度 (PSD) 估计值。
如果您将 spectrumtype 指定为 "power"，则 ps 的每列包含一个加窗段的功率谱估计值。

示例

[___] = spectrogram(___,"reassigned") 将每个 PSD 或功率谱估计值重新分配给其能量中心的位置。如果您的信号包含定位良好的时序分量或频谱分量，则此选项会生成更清晰的谱图。

示例

[___,ps,fc,tc] = spectrogram(___) 还返回两个矩阵 fc 和 tc，其中包含每个 PSD 或功率谱估计值的能量中心的频率和时间。

示例

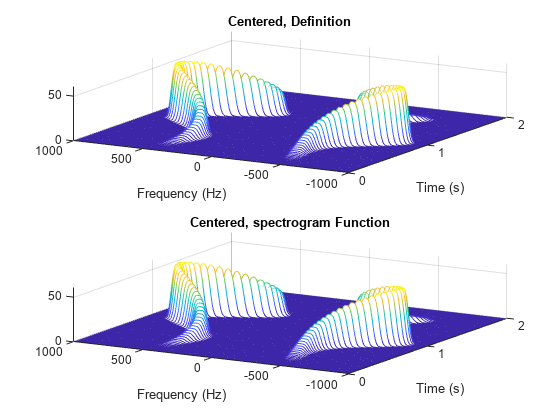
[___] = spectrogram(___,freqrange) 返回在 freqrange 指定的频率范围内的 PSD 或功率谱估计值。freqrange 的有效选项是 "onesided"、"twosided" 和 "centered"。

示例

[___] = spectrogram(___,Name=Value) 使用名称-值参量指定附加选项。选项包括最小阈值和输出时间维度。

示例

不带输出参量的 spectrogram(___) 在当前图窗窗口中绘制 ps（以分贝为单位）。

示例

spectrogram(___,freqloc) 指定绘制频率的轴。

示例

全部折叠

谱图的默认值

打开实时脚本

生成一个信号的 $N_{x} = 1024$ 个采样，该信号由正弦波之和组成。正弦波的归一化频率为 $2 π / 5$ 弧度/采样和 $4 π / 5$ 弧度/采样。较高频率正弦波的振幅是另一个正弦波的 10 倍。

N = 1024;
n = 0:N-1;

w0 = 2*pi/5;
x = sin(w0*n)+10*sin(2*w0*n);

使用函数默认值计算短时傅里叶变换。绘制谱图。

s = spectrogram(x);

spectrogram(x,'yaxis')

Figure contains an axes object. The axes object with xlabel Samples, ylabel Normalized Frequency ( times pi blank radians/sample) contains an object of type image.

重复该计算。

将信号分成长度为 $n s c = ⌊ N_{x} / 4.5 ⌋$ 的若干段。
使用汉明窗对这些段进行加窗处理。
指定连续段之间的重叠率为 50%。
为了计算 FFT，请使用 $\max (256, 2^{p})$ 个点，其中 $p = ⌈ \log_{2} n s c ⌉$ 。

验证这两种方法是否给出相同的结果。

Nx = length(x);
nsc = floor(Nx/4.5);
nov = floor(nsc/2);
nff = max(256,2^nextpow2(nsc));

t = spectrogram(x,hamming(nsc),nov,nff);

maxerr = max(abs(abs(t(:))-abs(s(:))))

maxerr = 
0

将信号分成 8 个等长的段，段之间的重叠率为 50%。指定与上一步相同的 FFT 长度。计算短时傅里叶变换，并验证它是否与前两个过程的结果相同。

ns = 8;
ov = 0.5;
lsc = floor(Nx/(ns-(ns-1)*ov));

t = spectrogram(x,lsc,floor(ov*lsc),nff);

maxerr = max(abs(abs(t(:))-abs(s(:))))

maxerr = 
0

比较 `spectrogram` 函数和 STFT 定义

打开实时脚本

生成一个信号，该信号由在 600 Hz 下采样 2 秒的复数值凸二次啁啾组成。啁啾的初始频率为 250 Hz，最终频率为 50 Hz。

fs = 6e2;
ts = 0:1/fs:2;
x = chirp(ts,250,ts(end),50,"quadratic",0,"convex","complex");

spectrogram 函数

使用 spectrogram 函数计算信号的 STFT。

将信号分成若干段，每段的长度为 $M = 49$ 个采样。
指定相邻段之间有 $L = 11$ 个采样的重叠。
丢弃最后的较短段。
使用巴特利窗对每个段加窗。
在 $N_{DFT} = 1024$ 个点的每个段计算离散傅里叶变换。默认情况下，spectrogram 计算复数值信号的双边变换。

M = 49;
L = 11;
g = bartlett(M);
Ndft = 1024;

[s,f,t] = spectrogram(x,g,L,Ndft,fs);

使用 waterplot 函数计算并显示谱图，定义为 STFT 的幅值平方。

waterplot(s,f,t)

Figure contains an axes object. The axes object with xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch.

STFT 定义

使用定义计算长度为 $N_{x}$ 个采样的信号的 STFT。将信号分成 $⌊ \frac{N_{x} - L}{M - L} ⌋$ 个重叠段。对每个段加窗并在 $N_{DFT}$ 个点处计算其离散傅里叶变换。

segs = framesig(1:length(x),M,OverlapLength=L);
X = fft(x(segs).*g,Ndft);

计算 STFT 的时间范围和频率范围。

要找到时间值，请将时间向量分成若干重叠段。时间值是段的中点，每个段被视为下端开放的区间。
要找到频率值，请指定在零频率处闭合、在下端开放的奈奎斯特区间。

framedT = ts(segs);
tint = mean(framedT(2:end,:));

fint = 0:fs/Ndft:fs-fs/Ndft;

将 spectrogram 的输出与定义进行比较。显示谱图。

maxdiff = max(max(abs(s-X)))

maxdiff = 
0

waterplot(X,fint,tint)

Figure contains an axes object. The axes object with xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch.

function waterplot(s,f,t)
% Waterfall plot of spectrogram
    waterfall(f,t,abs(s)'.^2)
    set(gca,XDir="reverse",View=[30 50])
    xlabel("Frequency (Hz)")
    ylabel("Time (s)")
end

比较 `spectrogram` 和 `stft` 函数

打开实时脚本

生成一个由在 1.4 kHz 下采样 2 秒的啁啾组成的信号。在测量时间内，啁啾的频率从 600 Hz 线性增加到 100 Hz。

fs = 1400;
x = chirp(0:1/fs:2,600,2,100);

stft 默认值

使用 spectrogram 和 stft 函数计算信号的 STFT。使用 stft 函数的默认值：

将信号分成若干长度为 128 个采样的段，并使用周期性汉宁窗对每个段加窗。
指定相邻段之间有 96 个采样的重叠。此长度等效于窗长度的 75%。
指定 128 个 DFT 点并将 STFT 中心设在零频率处，频率以赫兹为单位表示。

验证两个结果是否相等。

M = 128;
g = hann(M,"periodic");
L = 0.75*M;
Ndft = 128;

[sp,fp,tp] = spectrogram(x,g,L,Ndft,fs,"centered");

[s,f,t] = stft(x,fs);

dff = max(max(abs(sp-s)))

dff = 
0

使用 mesh 函数绘制两个输出。

nexttile
mesh(tp,fp,abs(sp).^2)
title("spectrogram")
view(2), axis tight

nexttile
mesh(t,f,abs(s).^2)
title("stft")
view(2), axis tight

Figure contains 2 axes objects. Axes object 1 with title spectrogram contains an object of type surface. Axes object 2 with title stft contains an object of type surface.

spectrogram 默认值

使用 spectrogram 函数的默认值重复计算：

将信号分成长度为 $M = ⌊ N_{x} / 4.5 ⌋$ 的段，其中 $N_{x}$ 是信号的长度。使用汉明窗对每个段加窗。
指定段之间有 50% 的重叠。
为了计算 FFT，请使用 $\max (256, 2^{⌈ \log_{2} M ⌉})$ 个点。仅计算正归一化频率的谱图。

M = floor(length(x)/4.5);
g = hamming(M);
L = floor(M/2);
Ndft = max(256,2^nextpow2(M));

[sx,fx,tx] = spectrogram(x);

[st,ft,tt] = stft(x,Window=g,OverlapLength=L, ...
    FFTLength=Ndft,FrequencyRange="onesided");

dff = max(max(sx-st))

dff = 
0

使用 waterplot 函数绘制两个输出。在这两种情况下都将频率轴除以 $π$ 。对于 stft 输出，将采样数除以有效采样率 $2 π$ 。

figure
nexttile
waterplot(sx,fx/pi,tx)
title("spectrogram")

nexttile
waterplot(st,ft/pi,tt/(2*pi))
title("stft")

$Figure contains 2 axes objects. Axes object 1 with title spectrogram, xlabel Frequency/\pi, ylabel Samples contains an object of type patch. Axes object 2 with title stft, xlabel Frequency/\pi, ylabel Samples contains an object of type patch.$

function waterplot(s,f,t)
% Waterfall plot of spectrogram
    waterfall(f,t,abs(s)'.^2)
    set(gca,XDir="reverse",View=[30 50])
    xlabel("Frequency/\pi")
    ylabel("Samples")
end

谱图和瞬时频率

打开实时脚本

使用 spectrogram 函数测量和跟踪信号的瞬时频率。

生成以 1 kHz 采样的时长为两秒的二次啁啾。指定啁啾的最初频率为 100 Hz，一秒后增加到 200 Hz。

fs = 1000;
t = 0:1/fs:2-1/fs;
y = chirp(t,100,1,200,'quadratic');

使用通过 spectrogram 函数实现的短时傅里叶变换来估计啁啾的频谱。将信号分成长度为 100 的段，使用汉明窗加窗。指定相邻段之间有 80 个采样的重叠，并在 $⌊ 100 / 2 + 1 ⌋ = 51$ 个频率处计算频谱。

spectrogram(y,100,80,100,fs,'yaxis')

Figure contains an axes object. The axes object with xlabel Time (s), ylabel Frequency (Hz) contains an object of type image.

通过找到在 $⌊ (2000 - 80) / (100 - 80) ⌋ = 96$ 个时间点上具有最高能量的时频脊来跟踪啁啾频率。在谱图上叠加瞬时频率。

[~,f,t,p] = spectrogram(y,100,80,100,fs);

[fridge,~,lr] = tfridge(p,f);

hold on
plot3(t,fridge,abs(p(lr)),'LineWidth',4)
hold off

Figure contains an axes object. The axes object with xlabel Time (s), ylabel Frequency (Hz) contains 2 objects of type image, line.

复信号的谱图

打开实时脚本

生成一个啁啾的 512 个采样，其频率成分呈正弦变化。

N = 512;
n = 0:N-1;

x = exp(1j*pi*sin(8*n/N)*32);

计算啁啾的居中双边短时傅里叶变换。将该信号分成若干长度为 32 个采样的段，段之间重叠 16 个采样。指定 64 个 DFT 点。绘制谱图。

[scalar,fs,ts] = spectrogram(x,32,16,64,'centered');

spectrogram(x,32,16,64,'centered','yaxis')

Figure contains an axes object. The axes object with xlabel Samples, ylabel Normalized Frequency ( times pi blank radians/sample) contains an object of type image.

通过在区间 $(- π, π]$ 上计算 64 个等间距频率的谱图获得相同的结果。'centered' 选项不是必需的。

fintv = -pi+pi/32:pi/32:pi;

[vector,fv,tv] = spectrogram(x,32,16,fintv);

spectrogram(x,32,16,fintv,'yaxis')

Figure contains an axes object. The axes object with xlabel Samples, ylabel Normalized Frequency ( times pi blank radians/sample) contains an object of type image.

比较 `spectrogram` 和 `pspectrum` 函数

打开实时脚本

生成一个由压控振荡器和三个高斯原子组成的信号。信号在 $f_{s} = 2$ kHz 下采样 2 秒。

fs = 2000;
tx = 0:1/fs:2;
gaussFun = @(A,x,mu,f) exp(-(x-mu).^2/(2*0.03^2)).*sin(2*pi*f.*x)*A';
s = gaussFun([1 1 1],tx',[0.1 0.65 1],[2 6 2]*100)*1.5;
x = vco(chirp(tx+.1,0,tx(end),3).*exp(-2*(tx-1).^2),[0.1 0.4]*fs,fs);
x = s+x';

短时傅里叶变换

使用 pspectrum 函数计算 STFT。

将 $N_{x}$ 采样信号分成长度为 $M = 80$ 个采样的段，对应的时间分辨率为 $80 / 2000 = 40$ 毫秒。
指定相邻段之间有 $L = 16$ 个采样或 20% 的重叠。
使用凯塞窗对每个段加窗，并指定泄漏 $ℓ = 0.7$ 。

M = 80;
L = 16;
lk = 0.7;

[S,F,T] = pspectrum(x,fs,"spectrogram", ...
    TimeResolution=M/fs,OverlapPercent=L/M*100, ...
    Leakage=lk);

与使用 spectrogram 函数获得的结果进行比较。

直接以采样为单位指定窗长度和重叠。
pspectrum 始终使用凯塞窗作为 $g (n)$ 。窗的泄漏 $ℓ$ 和形状因子 $β$ 的关系是 $β = 40 \times (1 - ℓ)$ 。
pspectrum 在计算离散傅里叶变换时始终使用 $N_{DFT} = 1024$ 个点。如果您要计算在双边或居中频率范围内的变换，可以指定此数字。但是，对于单边变换（实信号的默认变换），spectrogram 使用 $1024 / 2 + 1 = 513$ 个点。您也可以指定要在其上计算变换的频率向量，如此示例中所示。
如果信号无法精确分成 $k = ⌊ \frac{N_{x} - L}{M - L} ⌋$ 个段，spectrogram 会截断信号，而 pspectrum 会用零填充信号以创建一个额外的段。为了使输出等效，请删除最后一个段和时间向量的最后一个元素。
spectrogram 返回 STFT，其幅值平方是谱图。pspectrum 返回逐段功率谱，该功率谱已平方，但在平方之前除以因子 $\sum_{n} g (n)$ 。
对于单边变换，pspectrum 向谱图添加额外的因子 2。

g = kaiser(M,40*(1-lk));

k = (length(x)-L)/(M-L);
if k~=floor(k)
    S = S(:,1:floor(k));
    T = T(1:floor(k));
end

[s,f,t] = spectrogram(x/sum(g)*sqrt(2),g,L,F,fs);

使用 waterplot 函数显示由两个函数计算的谱图。

subplot(2,1,1)
waterplot(sqrt(S),F,T)
title("pspectrum")

subplot(2,1,2)
waterplot(s,f,t)
title("spectrogram")

Figure contains 2 axes objects. Axes object 1 with title pspectrum, xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch. Axes object 2 with title spectrogram, xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch.

maxd = max(max(abs(abs(s).^2-S)))

maxd = 
2.4419e-08

功率谱图和便捷图

spectrogram 函数有第四个参量，对应于逐段功率谱或功率谱密度。与 pspectrum 的输出类似，ps 参量已平方并包括归一化因子 $\sum_{n} g (n)$ 。对于实信号的单边谱图，您仍必须包括额外的因子 2。将函数的缩放参量设置为 "power"。

[~,~,~,ps] = spectrogram(x*sqrt(2),g,L,F,fs,"power");

max(abs(S(:)-ps(:)))

ans = 
2.4419e-08

当以不带输出参量形式被调用时，pspectrum 和 spectrogram 都以分贝为单位绘制信号的谱图。对于单边谱图，包括因子 2。将两个图的颜色图设置为相同。将 x 范围设置为相同的值，以使 pspectrum 图末尾的额外段可见。在 spectrogram 图中，在 y 轴上显示频率。

subplot(2,1,1)
pspectrum(x,fs,"spectrogram", ...
    TimeResolution=M/fs,OverlapPercent=L/M*100, ...
    Leakage=lk)
title("pspectrum")
cc = clim;
xl = xlim;

subplot(2,1,2)
spectrogram(x*sqrt(2),g,L,F,fs,"power","yaxis")
title("spectrogram")
clim(cc)
xlim(xl)

Figure contains 2 axes objects. Axes object 1 with title pspectrum, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image. Axes object 2 with title spectrogram, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.

function waterplot(s,f,t)
% Waterfall plot of spectrogram
    waterfall(f,t,abs(s)'.^2)
    set(gca,XDir="reverse",View=[30 50])
    xlabel("Frequency (Hz)")
    ylabel("Time (s)")
end

二次啁啾的重排的谱图

打开实时脚本

生成在 1 kHz 下采样 2 秒的啁啾信号。指定啁啾的最初频率为 100 Hz，1 秒后增加到 200 Hz。

fs = 1000;
t = 0:1/fs:2;
y = chirp(t,100,1,200,"quadratic");

估计重排后的信号谱图。

将信号分成长度为 128 的段，使用形状参数为 $β = 18$ 的凯塞窗加窗。
指定相邻段之间有 120 个采样的重叠。
在 $⌊ 128 / 2 ⌋ = 65$ 个频率和 $⌊ (l e n g t h (x) - 120) / (128 - 120) ⌋ = 235$ 个时间 bin 处计算频谱。

使用不带输出参量的 spectrogram 函数绘制重排后的谱图。在 y 轴上显示频率，在 x 轴上显示时间。

spectrogram(y,kaiser(128,18),120,128,fs, ...
    "reassigned","yaxis")

Figure contains an axes object. The axes object with xlabel Time (s), ylabel Frequency (Hz) contains an object of type image.

使用 imagesc 函数重新绘图。指定 y 轴方向，使频率值从下到上增大。向重排后的谱图添加 eps 以避免转换为分贝时可能出现的负无穷大。

[~,fr,tr,pxx] = spectrogram(y,kaiser(128,18),120,128,fs, ...
    "reassigned");

imagesc(tr,fr,pow2db(pxx+eps))
axis xy
xlabel("Time (s)")
ylabel("Frequency (Hz)")
colorbar

Figure contains an axes object. The axes object with xlabel Time (s), ylabel Frequency (Hz) contains an object of type image.

使用阈值的谱图

打开实时脚本

生成在 1 kHz 下采样 2 秒的啁啾信号。指定啁啾的最初频率为 100 Hz，1 秒后增加到 200 Hz。

Fs = 1000;
t = 0:1/Fs:2;
y = chirp(t,100,1,200,'quadratic');

估计信号的时间相关功率谱密度 (PSD)。

将信号分成长度为 128 的段，使用形状参数为 $β = 18$ 的凯塞窗加窗。
指定相邻段之间有 120 个采样的重叠。
在 $⌊ 128 / 2 ⌋ = 65$ 个频率和 $⌊ (l e n g t h (x) - 120) / (128 - 120) ⌋ = 235$ 个时间 bin 处计算频谱。

输出每个 PSD 估计值的重心的频率和时间。将小于 $- 30$ dB 的 PSD 元素设置为零。

[~,~,~,pxx,fc,tc] = spectrogram(y,kaiser(128,18),120,128,Fs, ...
    'MinThreshold',-30);

将非零元素绘制为重心频率和时间的函数。

plot(tc(pxx>0),fc(pxx>0),'.')

Figure contains an axes object. The axes contains a line object which displays its values using only markers.

计算居中和单边谱图

打开实时脚本

生成一个信号，该信号由在 2 kHz 下采样 2 秒的实数值啁啾组成。

fs = 2000;
tx = 0:1/fs:2;
x = vco(-chirp(tx,0,tx(end),2).*exp(-3*(tx-1).^2), ...
    [0.1 0.4]*fs,fs).*hann(length(tx))';

双边谱图

计算并绘制信号的双边 STFT。

将信号分成若干段，每段的长度为 $M = 73$ 个采样。
指定相邻段之间有 $L = 24$ 个采样的重叠。
丢弃最后的较短段。
使用平顶窗对每个段加窗。
在 $N_{DFT} = 895$ （注意这是奇数）个点的每个段处计算离散傅里叶变换。

M = 73;
L = 24;
g = flattopwin(M);
Ndft = 895;
neven = ~mod(Ndft,2);

[stwo,f,t] = spectrogram(x,g,L,Ndft,fs,"twosided");

使用不带输出参量的 spectrogram 函数绘制双边谱图。

spectrogram(x,g,L,Ndft,fs,"twosided","power","yaxis")

Figure contains an axes object. The axes object with xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.

使用定义计算双边谱图。将信号分成长度为 $M$ 个采样的段，相邻段之间有 $L$ 个采样的叠加。对每个段加窗并在 $N_{DFT}$ 个点处计算其离散傅里叶变换。

y = framesig(x,M,Window=g,OverlapLength=L);
Xtwo = fft(y,Ndft);

计算时间和频率范围。

要找到时间值，请将时间向量分成若干重叠段。时间值是段的中点，每个段被视为下端开放的区间。
要找到频率值，请指定在零频率处闭合、在上端开放的奈奎斯特区间。

framedT = framesig(tx,M,OverlapLength=L);
ttwo = mean(framedT(2:end,:));

ftwo = 0:fs/Ndft:fs*(1-1/Ndft);

将 spectrogram 的输出与定义进行比较。使用 waterplot 函数显示谱图。

diffs = [max(max(abs(stwo-Xtwo)));
    max(abs(f-ftwo'));
    max(abs(t-ttwo))]

diffs = 3×1
10^-12 ×

         0
    0.2274
    0.0002

figure
nexttile
waterplot(Xtwo,ftwo,ttwo)
title("Two-Sided, Definition")

nexttile
waterplot(stwo,f,t)
title("Two-Sided, spectrogram Function")

Figure contains 2 axes objects. Axes object 1 with title Two-Sided, Definition, xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch. Axes object 2 with title Two-Sided, spectrogram Function, xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch.

居中谱图

计算信号的居中谱图。

使用与用于双边 STFT 相同的时间值。
使用 fftshift 函数将 STFT 的零频率分量移至频谱中心。
对于奇数值 $N_{DFT}$ ，频率区间在两端开放。对于偶数值 $N_{DFT}$ ，频率区间在下端开放、在上端闭合。

比较输出并显示谱图。

tcen = ttwo;

if ~neven
    Xcen = fftshift(Xtwo,1);
    fcen = -fs/2*(1-1/Ndft):fs/Ndft:fs/2;
else
    Xcen = fftshift(circshift(Xtwo,-1),1);
    fcen = (-fs/2*(1-1/Ndft):fs/Ndft:fs/2)+fs/Ndft/2;
end

[scen,f,t] = spectrogram(x,g,L,Ndft,fs,"centered");

diffs = [max(max(abs(scen-Xcen)));
    max(abs(f-fcen'));
    max(abs(t-tcen))]

diffs = 3×1
10^-12 ×

         0
    0.2274
    0.0002

figure
nexttile
waterplot(Xcen,fcen,tcen)
title("Centered, Definition")

nexttile
waterplot(scen,f,t)
title("Centered, spectrogram Function")

Figure contains 2 axes objects. Axes object 1 with title Centered, Definition, xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch. Axes object 2 with title Centered, spectrogram Function, xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch.

单边谱图

计算信号的单边谱图。

使用与用于双边 STFT 相同的时间值。
对于奇数值 $N_{DFT}$ ，单边 STFT 由双边 STFT 的前 $(N_{DFT} + 1) / 2$ 行组成。对于偶数值 $N_{DFT}$ ，单边 STFT 由双边 STFT 的前 $N_{DFT} / 2 + 1$ 行组成。
对于奇数值 $N_{DFT}$ ，频率区间在零频率处闭合，在奈奎斯特频率处开放。对于偶数值 $N_{DFT}$ ，频率区间在两端闭合。

比较输出并显示谱图。对于实数值信号，"onesided" 参量是可选的。

tone = ttwo;

if ~neven
    Xone = Xtwo(1:(Ndft+1)/2,:);
else
    Xone = Xtwo(1:Ndft/2+1,:);
end

fone = 0:fs/Ndft:fs/2;

[sone,f,t] = spectrogram(x,g,L,Ndft,fs);

diffs = [max(max(abs(sone-Xone)));
    max(abs(f-fone'));
    max(abs(t-tone))]

diffs = 3×1
10^-12 ×

         0
    0.1137
    0.0002

figure
nexttile
waterplot(Xone,fone,tone)
title("One-Sided, Definition")

nexttile
waterplot(sone,f,t)
title("One-Sided, spectrogram Function")

Figure contains 2 axes objects. Axes object 1 with title One-Sided, Definition, xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch. Axes object 2 with title One-Sided, spectrogram Function, xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch.

function waterplot(s,f,t)
% Waterfall plot of spectrogram
waterfall(f,t,abs(s)'.^2)
set(gca,XDir="reverse",View=[30 50])
xlabel("Frequency (Hz)")
ylabel("Time (s)")
end

计算段 PSD 和功率谱

打开实时脚本

spectrogram 函数有一个矩阵作为第四个输出参量，该矩阵包含每个段的功率谱密度 (PSD) 或功率谱。功率谱等于 PSD 乘以窗的等效噪声带宽 (ENBW)。

生成一个信号，该信号由在 1 kHz 下采样 1 秒的对数啁啾组成。啁啾的初始频率为 400 Hz，在测量结束时降至 10 Hz。

fs = 1000;
tt = 0:1/fs:1-1/fs;
y = chirp(tt,400,tt(end),10,"logarithmic");

具有采样率的段 PSD 和功率谱

将信号分成若干长度为 102 个采样的段，并使用汉宁窗对每个段加窗。指定相邻段之间有 12 个采样的重叠，并指定 1024 个 DFT 点。

M = 102;
g = hann(M);
L = 12;
Ndft = 1024;

使用默认 PSD 频谱类型计算信号的谱图。输出 STFT 和段功率谱密度数组。

[s,f,t,p] = spectrogram(y,g,L,Ndft,fs);

使用指定为 "power" 的频谱类型重复计算。输出 STFT 和段功率谱数组。

[r,~,~,q] = spectrogram(y,g,L,Ndft,fs,"power");

验证在两种情况下谱图相同。使用频率的对数刻度绘制谱图。

max(max(abs(s).^2-abs(r).^2))

ans = 
0

waterfall(f,t,abs(s)'.^2)
set(gca,XScale="log",...
    XDir="reverse",View=[30 50])

Figure contains an axes object. The axes object contains an object of type patch.

验证功率谱等于功率谱密度乘以窗的 ENBW。

max(max(abs(q-p*enbw(g,fs))))

ans = 
1.1102e-16

验证段功率谱矩阵与谱图成正比。比例因子是窗元素之和的平方。

max(max(abs(s).^2-q*sum(g)^2))

ans = 
0

在归一化频率下分段计算 PSD 和功率谱

重复计算，但现在使用归一化频率。当您将采样率指定为 $2 π$ 时，结果相同。

[~,~,~,pn] = spectrogram(y,g,L,Ndft);
[~,~,~,qn] = spectrogram(y,g,L,Ndft,"power");

max(max(abs(qn-pn*enbw(g,2*pi))))

ans = 
1.1102e-16

跟踪音频信号中的啁啾

打开实时脚本

加载一个音频信号，其中包含两个递减啁啾和一个宽带飞溅声。计算短时傅里叶变换。将波形分成若干长度为 400 个采样的段，段之间重叠 300 个采样。绘制谱图。

load splat

% To hear, type soundsc(y,Fs)

sg = 400;
ov = 300;

spectrogram(y,sg,ov,[],Fs,"yaxis")
colormap bone

Figure contains an axes object. The axes object with xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.

使用 spectrogram 函数输出信号的功率谱密度 (PSD)。

[s,f,t,p] = spectrogram(y,sg,ov,[],Fs);

使用 medfreq 函数跟踪两个啁啾。为了找到更强的低频啁啾，将搜索范围限制为 100 Hz 以上的频率和宽带声音开始之前的时间。

f1 = f > 100;
t1 = t < 0.75;

m1 = medfreq(p(f1,t1),f(f1));

为了找到微弱的高频啁啾，将搜索范围限制为 2500 Hz 以上的频率和 0.3 秒到 0.65 秒之间的时间。

f2 = f > 2500;
t2 = t > 0.3 & t < 0.65;

m2 = medfreq(p(f2,t2),f(f2));

在谱图上叠加结果。将频率值除以 1000 以便以 kHz 表示。

hold on
plot(t(t1),m1/1000,LineWidth=4)
plot(t(t2),m2/1000,LineWidth=4)
hold off

Figure contains an axes object. The axes object with xlabel Time (s), ylabel Frequency (kHz) contains 3 objects of type image, line.

三维谱图可视化

打开实时脚本

生成以 10 kHz 采样、长度为两秒的信号。将信号的瞬时频率指定为时间的三角函数。

fs = 10e3;
t = 0:1/fs:2;
x1 = vco(sawtooth(2*pi*t,0.5),[0.1 0.4]*fs,fs);

计算并绘制信号的谱图。使用长度为 256、形状参数为 $β = 5$ 的凯塞窗。指定段与段之间有 220 个采样的重叠，并指定 512 个 DFT 点。在 y 轴上绘制频率。使用默认颜色图和视图。

spectrogram(x1,kaiser(256,5),220,512,fs,'yaxis')

Figure contains an axes object. The axes object with xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.

将视图更改为将谱图显示为瀑布图。将颜色图设置为 bone。

view(-45,65)
colormap bone

Figure contains an axes object. The axes object with xlabel Time (s), ylabel Frequency (kHz) contains an object of type surface.

在坐标区句柄和面板容器中绘制谱图

自 R2025a 起

打开实时脚本

在坐标区句柄和面板容器中绘制四个信号的谱图。当您使用不带输出参量的 spectrogram 时，函数返回具有功率谱密度 (PSD) 估计值的便利图。要在特定坐标区句柄或面板容器上重现此绘图，请使用目标 Parent 输入参量指定 spectrogram。

创建四个振荡信号，采样率为 10 kHz，持续三秒。

x1:锯齿形振荡信号
x2:指数衰减振荡信号
x3:复数正弦包络
x4:二次扫描啁啾

Fs = 10e3;
t = 0:1/Fs:3;
x1 = vco(sawtooth(2*pi*t,0.5),[0.1 0.4]*Fs,Fs);
x2 = vco(sin(2*pi*t).*exp(-t),[0.1 0.4]*Fs,Fs) ...
    + 0.01*sin(2*pi*0.25*Fs*t);
x3 = exp(1j*pi*sin(4*t)*Fs/10);
x4 = chirp(t,Fs/10,t(end),Fs/2.5,"quadratic");

定义用于计算信号谱图的设定：512 个 DFT 点，长度为 256 个采样的凯塞窗，长度为 220 个采样的重叠。

nfft = 512;
g = kaiser(256,5);
ol = 220;

在坐标区句柄中绘制谱图

在新图窗窗口的西南角和东北角创建两个坐标区句柄。

fig = figure;
ax1 = axes(fig,Position=[0.05 0.1 0.55 0.45]);
ax2 = axes(fig,Position=[0.55 0.7 0.42 0.28]);

分别在图窗的西南和东北坐标区中绘制信号 x1 和 x2 的功率谱。以默认三维视线查看 x1 的谱图。在 x2 的谱图中的 y 轴上显示频率。

spectrogram(x1,g,ol,nfft,Fs,"power",Parent=ax1);
view(ax1,3);
spectrogram(x2,g,ol,nfft,Fs,"power","yaxis",Parent=ax2);

Figure contains 2 axes objects. Axes object 1 with xlabel Frequency (kHz), ylabel Time (s) contains an object of type surface. Axes object 2 with xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.

在基于 UI 的坐标区句柄中绘制谱图

在新 UI 图窗窗口的西北角创建一个坐标区句柄。

uif = uifigure(Position=[100 100 720 540]);
ax3 = uiaxes(uif,'Position',[5 305 300 200]);

在图窗坐标区上绘制信号 x3 的 PSD 估计值。在 y 轴上显示频率，以 0 kHz 为中心。

spectrogram(x3,g,ol,nfft,Fs,"centered","yaxis",Parent=ax3);
title(ax3,"Spectrogram in UI Axes")

Figure contains an axes object. The axes object with title Spectrogram in UI Axes, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.

在面板容器中绘制谱图

在 UI 图窗窗口的东南角添加一个面板容器。

ax4 = uipanel(uif,Position=[300 5 400 325], ...
    Title="Spectrogram in UI Panel", ...
    BackgroundColor="white");

在该面板容器上绘制信号 x4 的 PSD 估计值。在 y 轴上显示频率。

spectrogram(x4,g,ol,nfft,Fs,"yaxis",Parent=ax4);

Figure contains 2 axes objects and another object of type uipanel. Axes object 1 with xlabel Time (s), ylabel Frequency (kHz) contains an object of type image. Axes object 2 with title Spectrogram in UI Axes, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.

输入参数

全部折叠

`x` — 输入信号
向量

输入信号，指定为行向量或列向量。

示例: cos(pi/4*(0:159))+randn(1,160) 用于指定嵌入高斯白噪声中的正弦波。

数据类型: single | double
复数支持: 是

`window` — 窗
正整数 | 向量 | `[]`

窗，指定为正整数或者指定为行向量或列向量。使用 window 将信号分成段：

如果 window 是整数，则 spectrogram 将 x 分成长度为 window 的段，并使用该长度的汉明窗对每个段加窗。
如果 window 是向量，则 spectrogram 将 x 分成与该向量长度相同的段，并使用 window 对每个段加窗。

如果 x 的长度无法精确地分成具有 noverlap 个重叠采样的整数段，则 x 会相应地截断。

如果您将 window 指定为空，则 spectrogram 使用汉明窗，使得 x 分成八个段，段之间具有 noverlap 个重叠采样。

有关可用窗的列表，请参阅加窗法。

示例: hann(N+1) 和 (1-cos(2*pi*(0:N)'/N))/2 都指定长度为 N + 1 的汉宁窗。

`noverlap` — 重叠采样的数量
非负整数 | `[]`

重叠采样数，指定为非负整数。

如果 window 是标量，则 noverlap 必须小于 window。
如果 window 是向量，则 noverlap 必须小于 window 的长度。

如果您将 noverlap 指定为空，则 spectrogram 使用在段之间生成 50% 重叠的数字。如果未指定段长度，则函数将 noverlap 设置为 ⌊N_x/4.5⌋，其中 N_x 是输入信号的长度，⌊⌋ 符号表示向下取整函数。

`nfft` — DFT 点数
正整数 | `[]`

DFT 点数，指定为正整数标量。如果您将 nfft 指定为空，则 spectrogram 将参数设置为 max(256,2^p)，其中 p = ⌈log₂ N_w⌉，⌈⌉ 符号表示向上取整函数，且

如果 window 是标量，则 N_w = window。
如果 window 是向量，则 N_w = length(window)。

`w` — 归一化频率
向量

归一化频率，指定为向量。w 必须包含至少两个元素，否则该函数会将其解释为 nfft。归一化频率的单位为弧度/采样。

示例: pi./[2 4]

数据类型: single | double

`f` — 周期性频率
向量

周期性频率，指定为向量。f 必须包含至少两个元素，否则该函数会将其解释为 nfft。f 的单位由采样率 fs 指定。

数据类型: single | double

`fs` — 采样率
1 Hz (默认) | 正标量

采样率，指定为正标量。采样率是单位时间内的采样数。如果时间单位是秒，则采样率的单位是赫兹。

`freqrange` — PSD 估计值的频率范围
`"onesided"` | `"twosided"` | `"centered"`

PSD 估计值的频率范围，指定为 "onesided"、"twosided" 或 "centered"。对于实数值信号，默认值为 "onesided"。对于复数值信号，默认值为 "twosided"，并且指定 "onesided" 会导致错误。

"onesided" - 返回实数输入信号的单边谱图。如果 nfft 是偶数，则 ps 有 nfft/2 + 1 行，并在区间 [0, π] 弧度/采样上计算。如果 nfft 是奇数，则 ps 有 (nfft + 1)/2 行，区间为 [0, π) 弧度/采样。如果您指定 fs，则区间分别为 [0, fs/2] 周期/单位时间和 [0, fs/2) 周期/单位时间。
"twosided" - 返回实数值或复数值信号的双边谱图。ps 有 nfft 行，并在区间 [0, 2π) 弧度/采样上计算。如果您指定 fs，则区间为 [0, fs) 周期/单位时间。
"centered" - 返回实数值或复数值信号的居中双边谱图。ps 有 nfft 行。如果 nfft 是偶数，则 ps 在区间 (–π, π] 弧度/采样上计算。如果 nfft 是奇数，则 ps 在 (–π, π) 弧度/采样上计算。如果您指定 fs，则区间分别为 (–fs/2, fs/2] 周期/单位时间和 (–fs/2, fs/2) 周期/单位时间。

数据类型: char | string

`spectrumtype` — 功率谱缩放
`"psd"` (默认) | `"power"`

功率谱缩放，指定为 "psd" 或 "power"。

省略 spectrumtype 或指定 "psd" 会返回功率谱密度。
指定 "power" 会按窗的等效噪声带宽对每个 PSD 估计值进行缩放。结果是在每个频率处功率的估计值。如果 "reassigned" 选项启用，函数会在重排之前在每个频率 bin 的宽度上对 PSD 进行积分。

数据类型: char | string

`freqloc` — 频率显示轴
`"xaxis"` (默认) | `"yaxis"`

频率显示轴，指定为 "xaxis" 或 "yaxis"。

"xaxis" - 在 x 轴上显示频率，在 y 轴上显示时间。
"yaxis" - 在 y 轴上显示频率，在 x 轴上显示时间。

如果带输出参量调用 spectrogram，则此参量将被忽略。

数据类型: char | string

名称-值参数

全部折叠

将可选参量对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

示例: spectrogram(x,100,OutputTimeDimension="downrows") 将 x 分成长度为 100 的段，并使用该长度的汉明窗对每个段加窗。谱图的输出时间维度沿行排列。

如果使用的是 R2021a 之前的版本，请使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: spectrogram(x,100,'OutputTimeDimension','downrows') 将 x 分成长度为 100 的段，并使用该长度的汉明窗对每个段加窗。谱图的输出时间维度沿行排列。

`MinThreshold` — 阈值
`-Inf` (默认) | 实数标量

阈值，指定为以分贝为单位的实数标量。spectrogram 将 s 的那些元素设置为零，使 10 log₁₀(s) ≤ thresh。

`OutputTimeDimension` — 输出时间维度
`"acrosscolumns"` (默认) | `"downrows"`

输出时间维度，指定为 "acrosscolumns" 或 "downrows"。如果希望将 s、ps、fc 和 tc 的时间维度沿行排列，频率维度沿列排列，请将此值设置为 "downrows"。如果希望将 s、ps、fc 和 tc 的时间维度沿列排列，频率维度沿行排列，请将此值设置为 "acrosscolumns"。如果不带输出参量调用该函数，则忽略此输入。

数据类型: char | string

`Parent` — 目标父级
`[]` (默认) | `Axes` 对象 | `UIAxes` 对象 | `Panel` 对象

自 R2025a 起

目标父级，指定为 Axes 对象、UIAxes 对象或 Panel 对象。

如果您指定 Parent，则 spectrogram 函数在指定的目标父级上将 PSD 或功率谱绘制为曲面图。即使您调用函数时带或不带输出参量，函数都会返回该绘图。
如果您未指定 Parent 且未指定输出参量，则 spectrogram 函数在当前坐标区或 gca 返回的图上将 PSD 或功率谱绘制为曲面图。

有关目标的详细信息，请参阅图形对象。有关 MATLAB^® 图形中父子关系的详细信息，请参阅图形对象层次结构。

数据类型: Axes | UIAxes | Panel

输出参量

全部折叠

`s` — 短时傅里叶变换
矩阵

短时傅里叶变换，以矩阵形式返回。时间按 s 的列从左到右递增排列，频率从 0 开始沿行递增排列。

如果 x 是长度为 N_x 的信号，则 s 有 k 列，其中
- k = ⌊(N_x – noverlap)/(window – noverlap)⌋（如果 window 为标量。）
- k = ⌊(N_x – noverlap)/(length(window) – noverlap)⌋（如果 window 为向量。）
如果 x 是实数且 nfft 是偶数，则 s 有 (nfft/2 + 1) 行。
如果 x 是实数且 nfft 是奇数，则 s 有 (nfft + 1)/2 行。
如果 x 是复数值，则 s 有 nfft 行。

注意

当 freqrange 设置为 "onesided" 时，spectrogram 输出正奈奎斯特范围内的 s 值，并且不保持总功率。

s 不受 "reassigned" 选项影响。

`w` — 归一化频率
向量

归一化频率，以向量形式返回。w 的长度等于 s 的行数。

`t` — 时刻
向量

时刻，以向量形式返回。t 中的时间值对应每个段的中点。

`f` — 周期性频率
向量

周期性频率，以向量形式返回。f 的长度等于 s 的行数。

`ps` — 功率谱密度或功率谱
矩阵

功率谱密度 (PSD) 或功率谱，以矩阵形式返回。

如果 x 是实数且 freqrange 未指定或设置为 "onesided"，则 ps 包含每个段的 PSD 或功率谱的单边修正周期图估计值。函数在所有频率（除了 0 和奈奎斯特频率）上将功率乘以 2 以保持总功率。
如果 x 是复数值或如果 freqrange 设置为 "twosided" 或 "centered"，则 ps 包含每个段的 PSD 或功率谱的双边修正周期图估计值。
如果您在 w 中指定归一化频率向量或在 f 中指定周期性频率向量，则 ps 包含在输入频率处计算的每个段的 PSD 或功率谱的修正周期图估计值。

`fc`, `tc` — 能量中心频率和时间
矩阵

能量中心频率和时间，以与短时傅里叶变换大小相同的矩阵形式返回。如果您未指定采样率，则 fc 的元素以归一化频率形式返回。

详细信息

全部折叠

短时傅里叶变换

短时傅里叶变换 (STFT) 用于分析非平稳信号的频率成分随时间变化的情况。STFT 的幅值平方称为信号的谱图时频表示。有关谱图以及如何使用 Signal Processing Toolbox™ 函数计算谱图的详细信息，请参阅Spectrogram Computation with Signal Processing Toolbox。

信号的 STFT 是通过将长度为 M 的分析窗 g(n) 滑过信号并计算每段加窗数据的离散傅里叶变换 (DFT) 来计算的。窗以 R 个采样的间隔跳过原始信号，等效于相邻段之间有 L = M – R 个采样的叠加。大多数窗函数在边缘处逐渐变细以避免频谱振铃。每个加窗段的 DFT 会添加到复数值矩阵中，该矩阵包含每个时间点和频率点处的幅值和相位。STFT 矩阵有

$k = ⌊ \frac{N_{x} - L}{M - L} ⌋$

列，其中 N_x 是信号 x(n) 的长度，⌊⌋ 符号表示向下取整函数。对于居中和双边变换，矩阵中的行数等于 N_DFT（DFT 点数）；对于实数值信号的单边变换，则等于接近 N_DFT/2 的奇数。

STFT 矩阵 $X (f) = [\begin{matrix} X_{1} (f) & X_{2} (f) & X_{3} (f) & \dots & X_{k} (f) \end{matrix}]$ 的第 m 列包含以时间 mR 为中心的加窗数据的 DFT：

$X_{m} (f) = \sum_{n = - \infty}^{\infty} x (n) g (n - m R) e^{- j 2 π f n} .$

提示

如果短时傅里叶变换有零值，则将其转换为分贝会导致出现负无穷大而无法绘制。为了避免这种可能出现的问题，当您不带输出参量调用 spectrogram 时，该函数会向短时傅里叶变换添加 eps。

参考

[1] Boashash, Boualem, ed. Time Frequency Signal Analysis and Processing: A Comprehensive Reference. Second edition. EURASIP and Academic Press Series in Signal and Image Processing. Amsterdam and Boston: Academic Press, 2016.

[2] Chassande-Motin, Éric, François Auger, and Patrick Flandrin. "Reassignment." In Time-Frequency Analysis: Concepts and Methods. Edited by Franz Hlawatsch and François Auger. London: ISTE/John Wiley and Sons, 2008.

[3] Fulop, Sean A., and Kelly Fitz. "Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications." Journal of the Acoustical Society of America. Vol. 119, January 2006, pp. 360–371.

[4] Oppenheim, Alan V., and Ronald W. Schafer, with John R. Buck. Discrete-Time Signal Processing. Second edition. Upper Saddle River, NJ: Prentice Hall, 1999.

[5] Rabiner, Lawrence R., and Ronald W. Schafer. Digital Processing of Speech Signals. Englewood Cliffs, NJ: Prentice-Hall, 1978.

扩展功能

全部展开

tall 数组
对行数太多而无法放入内存的数组进行计算。

spectrogram 函数支持 tall 数组，但存在以下使用说明和限制：

输入必须为 tall 列向量。
必须始终指定 window 参量。
OutputTimeDimension 必须始终指定并设置为 "downrows"。
不支持 reassigned 选项。
不支持不带输出参量的语法。

有关详细信息，请参阅tall 数组。

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

不支持 Parent 输入参量。
使用名称-值参量指定的参量必须为编译时常量。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

用法说明和限制：

使用名称-值参量指定的参量必须为编译时常量。
可变大小 window 必须为双精度。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

用法说明和限制：

不支持不带输出参量的语法。
频率向量必须均匀间隔。

有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

此函数完全支持 GPU 数组。有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

全部展开

R2025a: 在指定的父级目标中可视化函数输出

spectrogram 函数支持在以下目标父级对象之一中绘制功率谱密度 (PSD) 估计值或功率谱：Axes、UIAxes 或 Panel。

R2024a: 单精度可变大小窗输入的代码生成支持

spectrogram 函数支持单精度可变大小窗输入的代码生成。

R2023b: `spectrogram` 支持单精度数据和 GPU 代码生成

spectrogram 函数支持单精度输入和图形处理单元 (GPU) 的代码生成。您必须拥有 MATLAB Coder™ 和 GPU Coder™ 才能生成 CUDA^® 代码。

R2023a: 使用创建绘图实时编辑器任务可视化函数输出

现在，您可以使用创建绘图实时编辑器任务以交互方式显示 spectrogram 的输出。您可以选择不同图类型并设置可选参数。该任务还会自动生成代码，这些代码成为您的实时脚本的一部分。

另请参阅

App

信号分析器

函数

goertzel | istft | periodogram | pspectrum | pwelch | stft | xspectrogram

主题

外部网站

傅里叶分析（MathWorks 教学资源）

spectrogram

语法

说明

示例

谱图的默认值

比较 spectrogram 函数和 STFT 定义

比较 spectrogram 和 stft 函数

谱图和瞬时频率

复信号的谱图

比较 spectrogram 和 pspectrum 函数

二次啁啾的重排的谱图

使用阈值的谱图

计算居中和单边谱图

计算段 PSD 和功率谱

跟踪音频信号中的啁啾

三维谱图可视化

在坐标区句柄和面板容器中绘制谱图

输入参数

x — 输入信号 向量

window — 窗 正整数 | 向量 | []

noverlap — 重叠采样的数量 非负整数 | []

nfft — DFT 点数 正整数 | []

w — 归一化频率 向量

f — 周期性频率 向量

fs — 采样率 1 Hz (默认) | 正标量

freqrange — PSD 估计值的频率范围 "onesided" | "twosided" | "centered"

spectrumtype — 功率谱缩放 "psd" (默认) | "power"

freqloc — 频率显示轴 "xaxis" (默认) | "yaxis"

名称-值参数

MinThreshold — 阈值 -Inf (默认) | 实数标量

OutputTimeDimension — 输出时间维度 "acrosscolumns" (默认) | "downrows"

Parent — 目标父级 [] (默认) | Axes 对象 | UIAxes 对象 | Panel 对象

输出参量

s — 短时傅里叶变换 矩阵

w — 归一化频率 向量

t — 时刻 向量

f — 周期性频率 向量

ps — 功率谱密度或功率谱 矩阵

fc, tc — 能量中心频率和时间 矩阵

详细信息

短时傅里叶变换

提示

参考

扩展功能

tall 数组 对行数太多而无法放入内存的数组进行计算。

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成 使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

版本历史记录

R2025a: 在指定的父级目标中可视化函数输出

R2024a: 单精度可变大小窗输入的代码生成支持

R2023b: spectrogram 支持单精度数据和 GPU 代码生成

R2023a: 使用创建绘图实时编辑器任务可视化函数输出

另请参阅

App

函数

主题

外部网站

比较 `spectrogram` 函数和 STFT 定义

比较 `spectrogram` 和 `stft` 函数

比较 `spectrogram` 和 `pspectrum` 函数

`x` — 输入信号
向量

`window` — 窗
正整数 | 向量 | `[]`

`noverlap` — 重叠采样的数量
非负整数 | `[]`

`nfft` — DFT 点数
正整数 | `[]`

`w` — 归一化频率
向量

`f` — 周期性频率
向量

`fs` — 采样率
1 Hz (默认) | 正标量

`freqrange` — PSD 估计值的频率范围
`"onesided"` | `"twosided"` | `"centered"`

`spectrumtype` — 功率谱缩放
`"psd"` (默认) | `"power"`

`freqloc` — 频率显示轴
`"xaxis"` (默认) | `"yaxis"`

`MinThreshold` — 阈值
`-Inf` (默认) | 实数标量

`OutputTimeDimension` — 输出时间维度
`"acrosscolumns"` (默认) | `"downrows"`

`Parent` — 目标父级
`[]` (默认) | `Axes` 对象 | `UIAxes` 对象 | `Panel` 对象

`s` — 短时傅里叶变换
矩阵

`w` — 归一化频率
向量

`t` — 时刻
向量

`f` — 周期性频率
向量

`ps` — 功率谱密度或功率谱
矩阵

`fc`, `tc` — 能量中心频率和时间
矩阵

tall 数组
对行数太多而无法放入内存的数组进行计算。

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

GPU 代码生成
使用 GPU Coder™ 为 NVIDIA® GPU 生成 CUDA® 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

R2023b: `spectrogram` 支持单精度数据和 GPU 代码生成