stft

短时傅里叶变换

全页折叠

语法

s = stft(x)
s = stft(x,fs)
s = stft(x,ts)
s = stft(___,Name=Value)
[s,f] = stft(___)
[s,f,t] = stft(___)
stft(___)

说明

s = stft(x) 返回 x 的短时傅里叶变换 (STFT)。

示例

s = stft(x,fs) 使用采样率 fs 返回 x 的 STFT。

示例

s = stft(x,ts) 使用采样时间 ts 返回 x 的 STFT。

示例

s = stft(___,Name=Value) 使用名称-值参量指定附加选项。选项包括 FFT 窗和长度。这些参量可以添加到上述任一输入语法。

示例

[s,f] = stft(___) 返回在其上计算 STFT 的频率 f。

示例

[s,f,t] = stft(___) 返回在其上计算 STFT 的时间。

示例

不带输出参量的 stft(___) 在当前图窗窗口中以分贝为单位绘制 STFT 的幅值平方。

示例

示例

全部折叠

打开实时脚本

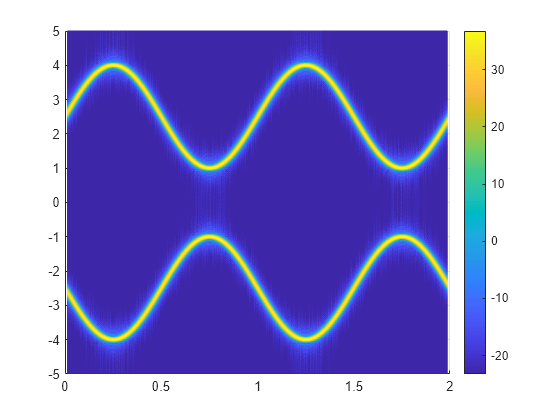
生成频率呈正弦变化的啁啾。信号以 10 kHz 频率进行 2 秒采样。

fs = 10e3;
t = 0:1/fs:2;
x = vco(sin(2*pi*t),[0.1 0.4]*fs,fs);

计算啁啾的短时傅里叶变换。将信号分成长度为 256 个采样的段，并使用形状参数 β = 5 的凯塞窗对每个段加窗。指定相邻段之间有 220 个采样的重叠，并指定 DFT 长度为 512。输出在其上计算 STFT 的频率和时间值。

[s,f,t] = stft(x,fs,Window=kaiser(256,5),OverlapLength=220,FFTLength=512);

STFT 的幅值平方也称为频谱图。以分贝为单位绘制频谱图。指定一个跨 60 dB 的颜色图，其最后颜色对应频谱图的最大值。

sdb = mag2db(abs(s));
mesh(t,f/1000,sdb);

cc = max(sdb(:))+[-60 0];
ax = gca;
ax.CLim = cc;
view(2)
colorbar

Figure contains an axes object. The axes object contains an object of type surface.

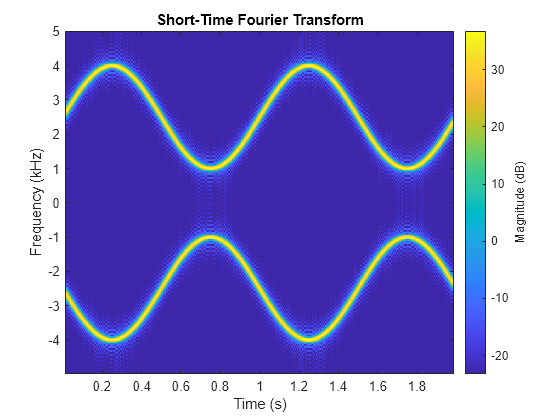
通过调用不带输出参量的 stft 函数获得相同的图。

stft(x,fs,Window=kaiser(256,5),OverlapLength=220,FFTLength=512)

Figure contains an axes object. The axes object with title Short-Time Fourier Transform, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.

打开实时脚本

生成以 1 kHz 进行 2 秒采样的二次啁啾。瞬时频率在 t=0 处为 100 Hz，并在 t=1 秒处超出 200 Hz。

ts = 0:1/1e3:2;

f0 = 100;
f1 = 200;

x = chirp(ts,f0,1,f1,"quadratic",[],"concave");

计算并显示持续 1 毫秒的二次啁啾的 STFT。

d = seconds(1e-3);
win = hamming(100,"periodic");

stft(x,d,Window=win,OverlapLength=98,FFTLength=128);

Figure contains an axes object. The axes object with title Short-Time Fourier Transform, xlabel Time (s), ylabel Frequency (Hz) contains an object of type image.

打开实时脚本

生成一个由在 1.4 kHz 下采样 2 秒的啁啾组成的信号。在测量时间内，啁啾的频率从 600 Hz 线性增加到 100 Hz。

fs = 1400;
x = chirp(0:1/fs:2,600,2,100);

stft 默认值

使用 spectrogram 和 stft 函数计算信号的 STFT。使用 stft 函数的默认值：

  • 将信号分成若干长度为 128 个采样的段，并使用周期性汉宁窗对每个段加窗。

  • 指定相邻段之间有 96 个采样的重叠。此长度等效于窗长度的 75%。

  • 指定 128 个 DFT 点并将 STFT 中心设在零频率处，频率以赫兹为单位表示。

验证两个结果是否相等。

M = 128;
g = hann(M,"periodic");
L = 0.75*M;
Ndft = 128;

[sp,fp,tp] = spectrogram(x,g,L,Ndft,fs,"centered");

[s,f,t] = stft(x,fs);

dff = max(max(abs(sp-s)))
dff = 
0

使用 mesh 函数绘制两个输出。

nexttile
mesh(tp,fp,abs(sp).^2)
title("spectrogram")
view(2), axis tight

nexttile
mesh(t,f,abs(s).^2)
title("stft")
view(2), axis tight

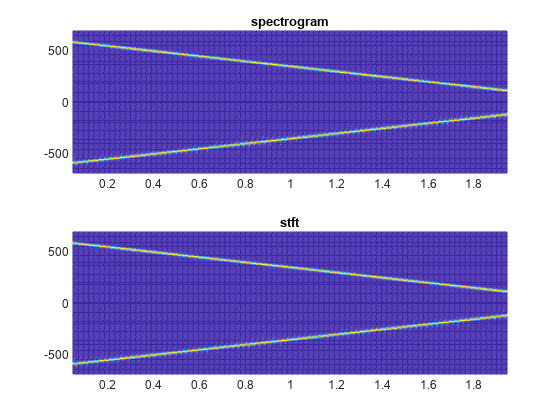
Figure contains 2 axes objects. Axes object 1 with title spectrogram contains an object of type surface. Axes object 2 with title stft contains an object of type surface.

spectrogram 默认值

使用 spectrogram 函数的默认值重复计算：

  • 将信号分成长度为 M=⌊Nx/4.5⌋ 的段，其中 Nx 是信号的长度。使用汉明窗对每个段加窗。

  • 指定段之间有 50% 的重叠。

  • 为了计算 FFT，请使用 max(256,2⌈log2M⌉) 个点。仅计算正归一化频率的频谱图。

M = floor(length(x)/4.5);
g = hamming(M);
L = floor(M/2);
Ndft = max(256,2^nextpow2(M));

[sx,fx,tx] = spectrogram(x);

[st,ft,tt] = stft(x,Window=g,OverlapLength=L, ...
    FFTLength=Ndft,FrequencyRange="onesided");

dff = max(max(sx-st))
dff = 
0

使用 waterplot 函数绘制两个输出。在这两种情况下都将频率轴除以 π。对于 stft 输出，将采样数除以有效采样率 2π。

figure
nexttile
waterplot(sx,fx/pi,tx)
title("spectrogram")

nexttile
waterplot(st,ft/pi,tt/(2*pi))
title("stft")

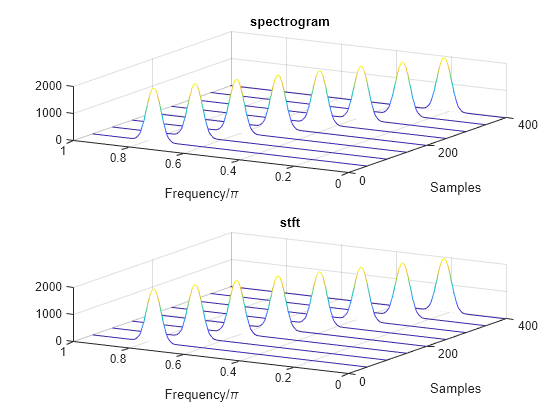
Figure contains 2 axes objects. Axes object 1 with title spectrogram, xlabel Frequency/\pi, ylabel Samples contains an object of type patch. Axes object 2 with title stft, xlabel Frequency/\pi, ylabel Samples contains an object of type patch.

function waterplot(s,f,t)
% Waterfall plot of spectrogram
    waterfall(f,t,abs(s)'.^2)
    set(gca,XDir="reverse",View=[30 50])
    xlabel("Frequency/\pi")
    ylabel("Samples")
end
打开实时脚本

生成一个信号，其采样率为 5 kHz，采样时间持续 4 秒。信号由一组持续时间递减的脉冲组成，各脉冲由振幅振荡和频率波动且呈递增趋势的区域分隔。绘制信号。

fs = 5000;
t = 0:1/fs:4-1/fs;

x = besselj(0,600*(sin(2*pi*(t+1).^3/30).^5));

plot(t,x)

Figure contains an axes object. The axes object contains an object of type line.

计算信号的单边、双边和居中短时傅里叶变换。在所有情况下，使用形状因子为 β=10 的长度为 202 个采样的凯塞窗对信号段加窗。显示用于计算每个变换的频率范围。

rngs = ["onesided" "twosided" "centered"];

for kj = 1:length(rngs)
    
    opts = {'Window',kaiser(202,10),'FrequencyRange',rngs(kj)};

    [~,f] = stft(x,fs,opts{:});
    subplot(length(rngs),1,kj)
    stft(x,fs,opts{:})
    title(sprintf('''%s'': [%5.3f, %5.3f] kHz',rngs(kj),[f(1) f(end)]/1000))

end

Figure contains 3 axes objects. Axes object 1 with title 'onesided': [0.000, 2.500] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image. Axes object 2 with title 'twosided': [0.000, 4.975] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image. Axes object 3 with title 'centered': [-2.475, 2.500] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.

重复计算，但现在将凯塞窗的长度更改为奇数 203。'twosided' 频率区间不变。其他两个频率区间在高端变为开放。

for kj = 1:length(rngs)
    
    opts = {'Window',kaiser(203,10),'FrequencyRange',rngs(kj)};

    [~,f] = stft(x,fs,opts{:});
    subplot(length(rngs),1,kj)
    stft(x,fs,opts{:})
    title(sprintf('''%s'': [%5.3f, %5.3f] kHz',rngs(kj),[f(1) f(end)]/1000))

end

Figure contains 3 axes objects. Axes object 1 with title 'onesided': [0.000, 2.488] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image. Axes object 2 with title 'twosided': [0.000, 4.975] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image. Axes object 3 with title 'centered': [-2.488, 2.488] kHz, xlabel Time (s), ylabel Frequency (kHz) contains an object of type image.

打开实时脚本

生成一个三通道信号，该信号由在 1 kHz 下采样一秒的三个不同啁啾组成。

  1. 第一个通道由凹二次啁啾组成，瞬时频率在 t = 0 处为 100 Hz，在 t = 1 秒处超出 300 Hz。其初始相位等于 45 度。

  2. 第二个通道由凸二次啁啾组成，瞬时频率在 t = 0 处为 100 Hz，在 t = 1 秒处超出 500 Hz。

  3. 第三个通道由对数啁啾组成，瞬时频率在 t = 0 处为 300 Hz，在 t = 1 秒处超出 500 Hz。

使用长度为 128 的周期性汉明窗和 50 个采样的重叠长度计算多通道信号的 STFT。

fs = 1e3;
t = 0:1/fs:1-1/fs;

x = [chirp(t,100,1,300,'quadratic',45,'concave');
      chirp(t,100,1,500,'quadratic',[],'convex');
      chirp(t,300,1,500,'logarithmic')]'; 
  
[S,F,T] = stft(x,fs,'Window',hamming(128,'periodic'),'OverlapLength',50);

将每个通道的 STFT 可视化为瀑布图。使用辅助函数 helperGraphicsOpt 控制坐标区的行为。

waterfall(F,T,abs(S(:,:,1))')
helperGraphicsOpt(1)

Figure contains an axes object. The axes object with title Input Channel: 1, xlabel Frequency (Hz), ylabel Time (seconds) contains an object of type patch.

waterfall(F,T,abs(S(:,:,2))')
helperGraphicsOpt(2)

Figure contains an axes object. The axes object with title Input Channel: 2, xlabel Frequency (Hz), ylabel Time (seconds) contains an object of type patch.

waterfall(F,T,abs(S(:,:,3))')
helperGraphicsOpt(3)

Figure contains an axes object. The axes object with title Input Channel: 3, xlabel Frequency (Hz), ylabel Time (seconds) contains an object of type patch.

此辅助函数设置当前坐标区的外观和行为。

function helperGraphicsOpt(ChannelId)
ax = gca;
ax.XDir = 'reverse';
ax.ZLim = [0 30];
ax.Title.String = ['Input Channel: ' num2str(ChannelId)];
ax.XLabel.String = 'Frequency (Hz)';
ax.YLabel.String = 'Time (seconds)';
ax.View = [30 45];
end

输入参数

全部折叠

输入信号，指定为向量、矩阵或 MATLAB® timetable。

注意

如果您需要 x 和 s 长度相同，则 (length(x)-noverlap)/(length(window)-noverlap) 的值必须为整数。使用 Window 指定 window 的长度，使用 OverlapLength 指定 noverlap。

  • 如果输入有多个通道，请将 x 指定为矩阵，其中每列对应一个通道。

  • 对于时间表输入，x 必须包含均匀递增的有限行时间。如果时间表有缺失或重复的时间点，您可以使用清理包含缺失、重复或不均匀时间的时间表中的提示进行修复。

  • 对于多通道时间表输入，将 x 指定为具有单个变量（其中包含一个矩阵）的时间表，或指定为具有多个变量（其中每个变量包含一个列向量）的时间表。所有变量必须具有相同的精度。

x 的每个通道的长度必须大于或等于窗长度。

示例: chirp(0:1/4e3:2,250,1,500,"quadratic") 指定一个单通道啁啾。

示例: timetable(rand(5,2),SampleRate=1) 指定一个在 1 Hz 下采样 4 秒的双通道随机变量。

示例: timetable(rand(5,1),rand(5,1),SampleRate=1) 指定一个在 1 Hz 下采样 4 秒的双通道随机变量。

数据类型: double | single
复数支持: 是

采样率，指定为正标量。此参量仅当 x 是向量或矩阵时适用。

数据类型: double | single

采样时间，指定为 duration 标量。此参量仅当 x 是向量或矩阵时适用

示例: seconds(1) 是 duration 标量，表示连续信号采样之间有 1 秒时间差。

数据类型: duration

名称-值参数

全部折叠

将可选参量对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

示例: Window=hamming(100),OverlapLength=50,FFTLength=128 使用长度为 100 个采样的汉明窗对数据加窗，相邻段之间有 50 个采样的重叠且 FFT 包含 128 个点。

如果使用的是 R2021a 之前的版本，请使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: 'Window',hamming(100),'OverlapLength',50,'FFTLength',128 使用长度为 100 个采样的汉明窗对数据加窗，相邻段之间有 50 个采样的重叠且 FFT 包含 128 个点。

频谱窗，指定为向量。如果您未指定窗或将其指定为空，则函数使用长度为 128 的汉宁窗。Window 的长度必须大于或等于 2。

有关可用窗的列表，请参阅加窗法。

示例: hann(N+1) 和 (1-cos(2*pi*(0:N)'/N))/2 都指定长度为 N + 1 的汉宁窗。

数据类型: double | single

重叠采样的数量，指定为小于 Window 长度的正整数。如果您省略 OverlapLength 或将其指定为空，则它设置为小于窗长度的 75% 的最大整数，对于默认汉宁窗为 96 个采样。

数据类型: double | single

DFT 点数，指定为正整数。该值必须大于或等于窗长度。如果输入信号的长度小于 DFT 长度，则数据用零填充。

数据类型: double | single

STFT 频率范围，指定为 "centered"、"twosided" 或 "onesided"。

  • "centered" - 计算一个双边、居中 STFT。如果 FFTLength 是偶数，则 s 在区间 (–π, π] 弧度/采样点上计算。如果 FFTLength 是奇数，则 s 在区间 (–π, π) 弧度/采样点上计算。如果您指定时间信息，则区间分别为 (–fs, fs/2] 周期/单位时间和 (–fs, fs/2) 周期/单位时间，其中 fs 是有效采样率。

  • "twosided" - 在区间 [0, 2π) 弧度/采样点上计算双边 STFT。如果您指定时间信息，则区间为 [0, fs) 周期/单位时间。

  • "onesided" - 计算单边 STFT。如果 FFTLength 是偶数，则 s 在区间 [0, π] 弧度/采样点上计算。如果 FFTLength 是奇数，则 s 在区间 [0, π) 弧度/采样点上计算。如果您指定时间信息，则区间分别为 [0, fs/2] 周期/单位时间和 [0, fs/2) 周期/单位时间，其中 fs 是有效采样率。此选项仅对实信号有效。

    注意

    当此参量设置为 "onesided" 时，stft 输出正奈奎斯特范围内的值，并且不保持总功率。

有关示例，请参阅STFT 频率范围。

数据类型: char | string

输出时间维度，指定为 "acrosscolumns" 或 "downrows"。如果希望将 s 的时间维度沿行排列，频率维度沿列排列，请将此值设置为 "downrows"。如果希望将 s 的时间维度沿列排列，频率维度沿行排列，请将此值设置为 "acrosscolumns"。如果不带输出参量调用该函数，则忽略此输入。

输出参量

全部折叠

短时傅里叶变换，以矩阵或三维数组形式返回。时间按 s 的列从左到右递增，频率按行从上到下递增。第三个维度（如果存在）对应一个输入通道。

  • 如果信号 x 有 Nx 个时间采样，则 s 有 k 列，其中 k = ⌊(Nx–L)/(M–L)⌋，M 是 Window 的长度，L 是 OverlapLength，⌊ ⌋ 符号表示向下取整函数。

  • s 中的行数等于在 FFTLength 中指定的值。

数据类型: double | single

在其上计算 STFT 的频率，以向量形式返回。

数据类型: double | single

时刻，以向量形式返回。t 包含时间值，这些时间值对应于用于估计短时功率谱估计值的数据段中心。

  • 如果提供了采样率 fs，则向量包含以秒为单位的时间值。

  • 如果提供了采样时间 ts，则向量是持续时间数组，具有与输入相同的时间格式。

  • 如果未提供时间信息，则向量包含采样编号。

数据类型: double | single

详细信息

全部折叠

参考

[1] Mitra, Sanjit K. Digital Signal Processing: A Computer-Based Approach. 2nd Ed. New York: McGraw-Hill, 2001.

[2] Sharpe, Bruce. Invertibility of Overlap-Add Processing. https://gauss256.github.io/blog/cola.html, accessed July 2019.

[3] Smith, Julius Orion. Spectral Audio Signal Processing. https://ccrma.stanford.edu/~jos/sasp/, online book, 2011 edition, accessed Nov 2018.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

版本历史记录

在 R2019a 中推出

另请参阅

函数

对象

主题