Main Content

dlstft

Deep learning short-time Fourier transform

Since R2021a

collapse all in page

Syntax

y = dlstft(x)
y = dlstft(x,fs)
y = dlstft(x,ts)
y = dlstft(___,Name,Value)
[y,f,t] = dlstft(___)

Description

y = dlstft(x) returns the deep learning Short-Time Fourier Transform (STFT) of x. dlstft requires Deep Learning Toolbox™.

example

y = dlstft(x,fs) returns the deep learning STFT assuming that x was sampled at the rate fs.

example

y = dlstft(x,ts) returns the deep learning STFT assuming that x was sampled with sample time ts.

example

y = dlstft(___,Name,Value) specifies additional options using name-value arguments. Options include the spectral window and the FFT length. These arguments can be added to any of the previous input syntaxes. For example, 'DataFormat','CBT' specifies the data format of x as CBT.

example

[y,f,t] = dlstft(___) returns the frequencies f and times t at which the deep learning STFT is computed.

example

Examples

collapse all

This example uses:

Open Live Script

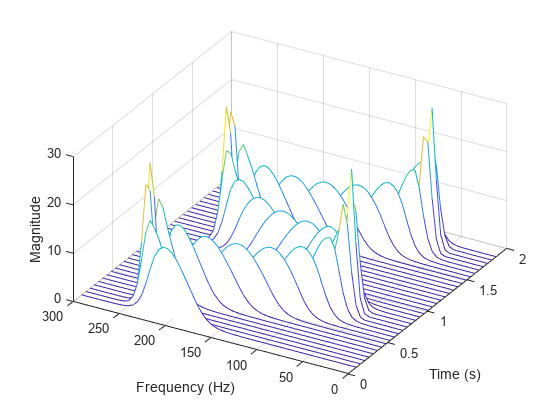
Generate a signal sampled at 600 Hz for 2 seconds. The signal consists of a chirp with sinusoidally varying frequency content.

fs = 6e2;
t = 0:1/fs:2;
x = vco(sin(2*pi*t),[0.1 0.4]*fs,fs);

Store the signal in an unformatted deep learning array. Compute the short-time Fourier transform of the signal. Input the sample time as a duration scalar. (Alternatively, input the sample rate as a numeric scalar.) Specify that the input array is in 'CTB' format.

dlx = dlarray(x);

[y,f,t] = dlstft(dlx,seconds(1/fs),'DataFormat','CTB');

Convert the outputs to numeric arrays. Compute the magnitude of the short-time Fourier transform and display it as a waterfall plot.

y = extractdata(y);
f = extractdata(f);
t = seconds(t);

waterfall(f,t,squeeze(abs(y))')

ax = gca;
ax.XDir = 'reverse';
view(30,45)

ylabel('Time (s)')
xlabel('Frequency (Hz)')
zlabel('Magnitude')

Figure contains an axes object. The axes object with xlabel Frequency (Hz), ylabel Time (s) contains an object of type patch.

This example uses:

Open Live Script

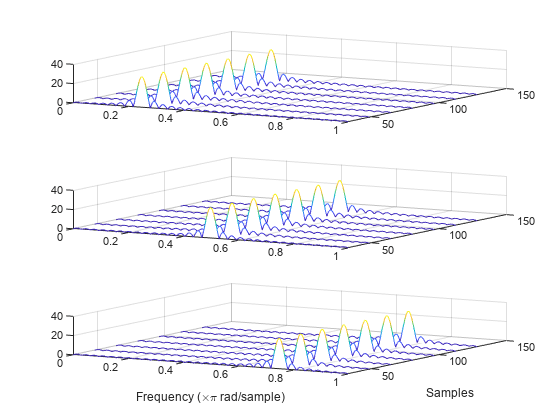
Generate a 3-by-160(-by-1) array containing one batch of a three-channel, 160-sample sinusoidal signal. The normalized sinusoid frequencies are π/4 rad/sample, π/2 rad/sample, and 3π/4 rad/sample. Save the signal as a dlarray, specifying the dimensions in order. dlarray permutes the array dimensions to the 'CBT' shape expected by a deep learning network. Display the array dimension sizes.

x = dlarray(cos(pi.*(1:3)'/4*(0:159)),'CTB');
[nchan,nbtch,nsamp] = size(x)
nchan = 
3

nbtch = 
1

nsamp = 
160

Compute the deep learning short-time Fourier transform of the signal. Specify a 64-sample rectangular window and an FFT length of 1024.

[y,f,t] = dlstft(x,'Window',rectwin(64),'FFTLength',1024);

dlstft computes the transform along the 'T' dimension. The output array is in 'SCBT' format. The 'S' dimension corresponds to frequency in the short-time Fourier transform. Extract the data from the deep learning array.

y = extractdata(y);
f = extractdata(f);
t = extractdata(t);

Compute the magnitude of the short-time Fourier transform. Plot the magnitude separately for each channel in a waterfall plot.

z = abs(squeeze(y));

for kj = 1:nchan
    subplot(nchan,1,kj)
    waterfall(f/pi,t,squeeze(z(:,kj,:))')
    view(30,45)
end

xlabel('Frequency (\times\pi rad/sample)')
ylabel('Samples')

Figure contains 3 axes objects. Axes object 1 contains an object of type patch. Axes object 2 contains an object of type patch. Axes object 3 with xlabel Frequency (\times\pi rad/sample), ylabel Samples contains an object of type patch.

Input Arguments

collapse all

Input array, specified as an unformatted dlarray (Deep Learning Toolbox) object, a formatted dlarray object in 'CBT' format, or a numeric array. If x is an unformatted dlarray or a numeric array, you must specify the 'DataFormat' as some permutation of 'CBT'.

Example: dlarray(cos(pi./[4;2]*(0:159)),'CTB') and dlarray(cos(pi./[4;2]*(0:159))','TCB') both specify one batch observation of a two-channel sinusoid in the 'CBT' format.

Sample rate, specified as a positive numeric scalar.

Sample time, specified as duration scalar. Specifying ts is equivalent to setting a sample rate fs = 1/ts.

Example: seconds(1) is a duration scalar representing a 1-second time difference between consecutive signal samples.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Window',hamming(100),'OverlapLength',50,'FFTLength',128 windows the data using a 100-sample Hamming window, with 50 samples of overlap between adjoining segments and a 128-point FFT.

Input data format, specified as a character vector or string scalar. This argument is valid only if x is unformatted.

Each character in this argument must be one of these labels:

  • C — Channel

  • B — Batch observations

  • T — Time

The dlstft function accepts any permutation of 'CBT'. You can specify at most one of each of the C, B, and T labels.

Each element of the argument labels the matching dimension of x. If the argument is not in the listed order ('C' followed by 'B' and so on), then dlstft implicitly permutes both the argument and the data to match the order, but without changing how the data is stored.

Example: 'CBT'

Spectral window, specified as a vector. If you do not specify the window or specify it as empty, the function uses a Hann window of length 128. The length of 'Window' must be greater than or equal to 2.

For a list of available windows, see Windows.

Example: hann(N+1) and (1-cos(2*pi*(0:N)'/N))/2 both specify a Hann window of length N + 1.

Data Types: double | single

Number of overlapped samples, specified as a nonnegative integer smaller than the length of 'Window'. If you omit 'OverlapLength' or specify it as empty, it is set to the largest integer less than 75% of the window length, which is 96 samples for the default Hann window.

Data Types: double | single

Number of DFT points, specified as a positive integer. The value must be greater than or equal to the window length. If the length of the input signal is less than the DFT length, the data is padded with zeros.

Data Types: double | single

Output Arguments

collapse all

Short-time Fourier transform, returned as a formatted or unformatted dlarray (Deep Learning Toolbox) object.

  • If x is a formatted dlarray, then y is an 'SCBT' formatted dlarray object. The 'S' dimension corresponds to frequency in the short-time Fourier transform.

  • If x is an unformatted dlarray or a numeric array, then y is an unformatted dlarray object. The dimension order in y is 'SCBT'.

If no time information is specified, then the STFT is computed over the Nyquist range [0, π] if 'FFTLength' is even and over [0, π) if 'FFTLength' is odd. If you specify time information, then the intervals are [0, fs/2] and [0, fs/2), respectively, where fs is the effective sample rate.

Frequencies at which the deep learning STFT is computed, returned as a dlarray object.

  • If the input array does not contain time information, then the frequencies are in normalized units of rad/sample.

  • If the input array contains time information, then f contains frequencies expressed in Hz.

Times at which the deep learning STFT is computed, returned as a dlarray object or a duration array.

  • If you do not specify time information, then t contains sample numbers.

  • If you specify a sample rate, then t contains time values in seconds.

  • If you specify a sample time, then t is a duration array with the same time format as x.

More About

collapse all

Short-Time Fourier Transform

The short-time Fourier transform (STFT) is used to analyze how the frequency content of a nonstationary signal changes over time. The magnitude squared of the STFT is known as the spectrogram time-frequency representation of the signal. For more information about the spectrogram and how to compute it using Signal Processing Toolbox™ functions, see Spectrogram Computation with Signal Processing Toolbox.

The STFT of a signal is computed by sliding an analysis window g(n) of length M over the signal and calculating the discrete Fourier transform (DFT) of each segment of windowed data. The window hops over the original signal at intervals of R samples, equivalent to L = M – R samples of overlap between adjoining segments. Most window functions taper off at the edges to avoid spectral ringing. The DFT of each windowed segment is added to a complex-valued matrix that contains the magnitude and phase for each point in time and frequency. The STFT matrix has

k=⌊Nx−LM−L⌋

columns, where Nx is the length of the signal x(n) and the ⌊⌋ symbols denote the floor function. The number of rows in the matrix equals NDFT, the number of DFT points, for centered and two-sided transforms and an odd number close to NDFT/2 for one-sided transforms of real-valued signals.

The mth column of the STFT matrix X(f)=[X1(f)X2(f)X3(f)⋯Xk(f)] contains the DFT of the windowed data centered about time mR:

Xm(f)=∑n=−∞∞x(n) g(n−mR) e−j2πfn.

Figure shows the short time Fourier transform sequence. On top, there is a signal in time domain x(n). Segmentation windowing follows below, partitioning x(n) into segments. Upon applying the Fourier transform to the signal segments, they altogether form the squared of the absolute value of X(f), the time-frequency domain equivalent of x(n).

Extended Capabilities

Version History

Introduced in R2021a

expand all

See Also

Objects

Functions

Topics