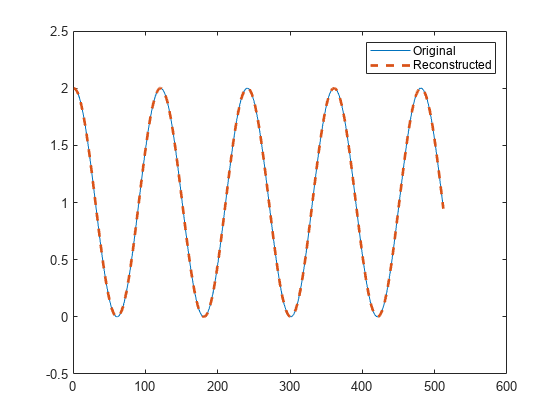
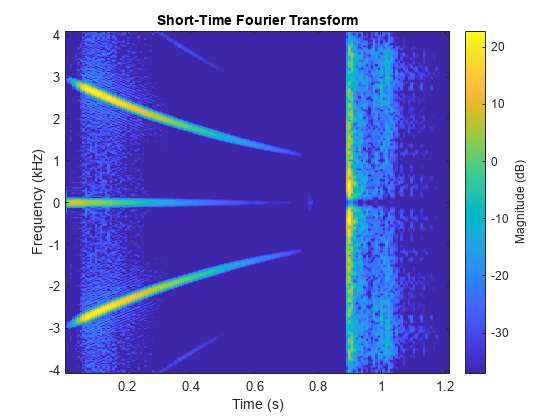
stftmag2sig
Signal reconstruction from STFT magnitude
Syntax
Description
x = stftmag2sig(s,nfft)x, estimated from
the Short-Time Fourier Transform (STFT) magnitude,
s, based on the Griffin-Lim algorithm. The function assumes
s was computed using discrete Fourier transform (DFT) length
nfft.
x = stftmag2sig(___,Name=Value)FrequencyRange="onesided",InitializePhaseMethod="random" specifies
that the signal is reconstructed from a one-sided STFT with random initial phases.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
More About
Tips
If you are using the gradient descent method and the reconstruction is not satisfactory, set
Displaytotrue. Observe the inconsistency during iterations. If the inconsistency does not decrease, reduceStepSizefor better reconstruction.If you are using the gradient descent method, the L-BFGS optimizer usually provides the best results. This optimizer automatically selects the step size for each iteration. However, the L-BFGS optimizer may require more computation time than other optimizers to run the same number of iterations.
References
[1] Griffin, Daniel W., and Jae S. Lim. "Signal Estimation from Modified Short-Time Fourier Transform." IEEE Transactions on Acoustics, Speech, and Signal Processing. Vol. 32, Number 2, April 1984, pp. 236–243. https://doi.org/10.1109/TASSP.1984.1164317.
[2] Perraudin, Nathanaël, Peter Balazs, and Peter L. Søndergaard. "A Fast Griffin-Lim Algorithm." In 2013 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, October 20–23, 2013. https://doi.org/10.1109/WASPAA.2013.6701851.
[3] Le Roux, Jonathan, Hirokazu Kameoka, Nobutaka Ono, and Shigeki Sagayama. "Fast Signal Reconstruction from Magnitude STFT Spectrogram Based on Spectrogram Consistency." In Proceedings of the 13th International Conference on Digital Audio Effects (DAFx-10), Graz, Austria, September 6–10, 2010.
[4] Ji, Li, and Zhou Tie. “On Gradient Descent Algorithm for Generalized Phase Retrieval Problem.” In 2016 IEEE 13th International Conference on Signal Processing (ICSP), 320–25. Chengdu, China: IEEE, 2016. https://doi.org/10.1109/ICSP.2016.7877848.