rpmfreqmap
Frequency-RPM map for order analysis
Syntax
Description
map = rpmfreqmap(x,fs,rpm)map, that results
from performing frequency analysis on the input vector, x. x is
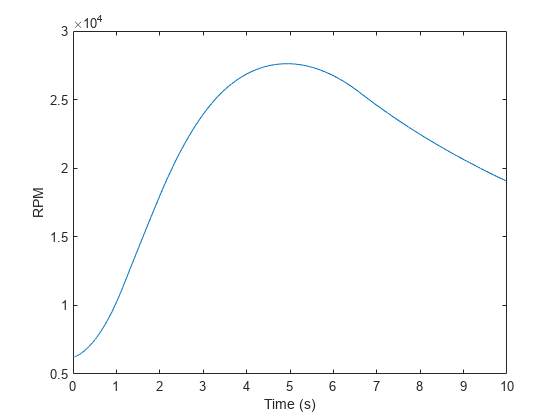
measured at a set rpm of rotational speeds expressed
in revolutions per minute. fs is the sample rate
in Hz. Each column of map contains root-mean-square
(RMS) amplitude estimates of the spectral content present at each
value of rpm. rpmfreqmap uses
the short-time Fourier transform to analyze the spectral content of x.
map = rpmfreqmap(___,Name,Value)Name,Value pairs in addition to
the input arguments in previous syntaxes.
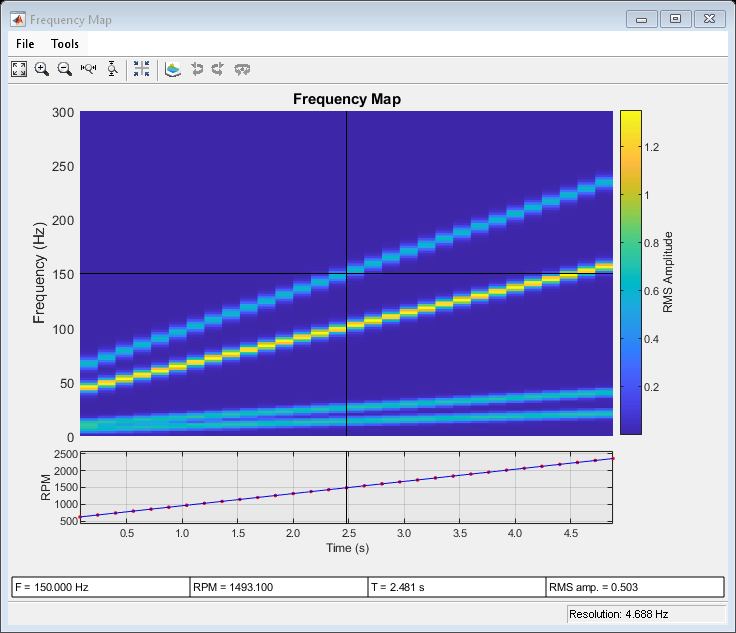
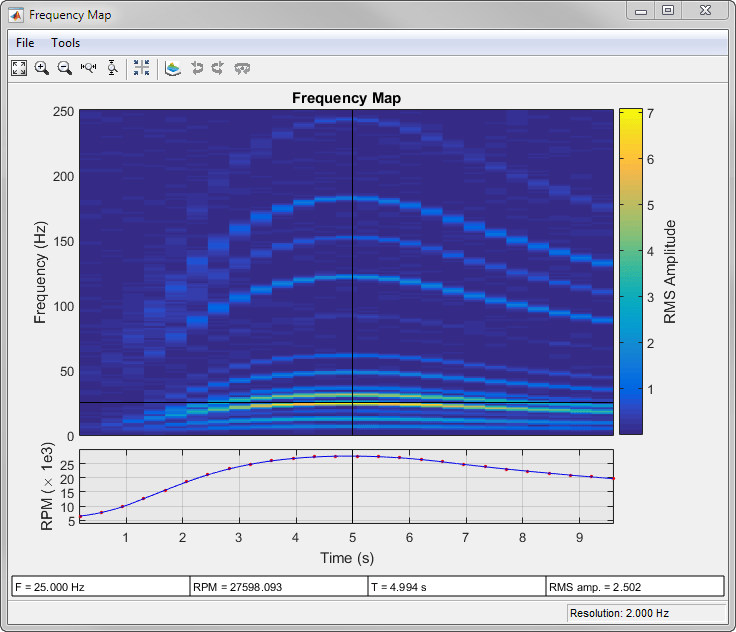
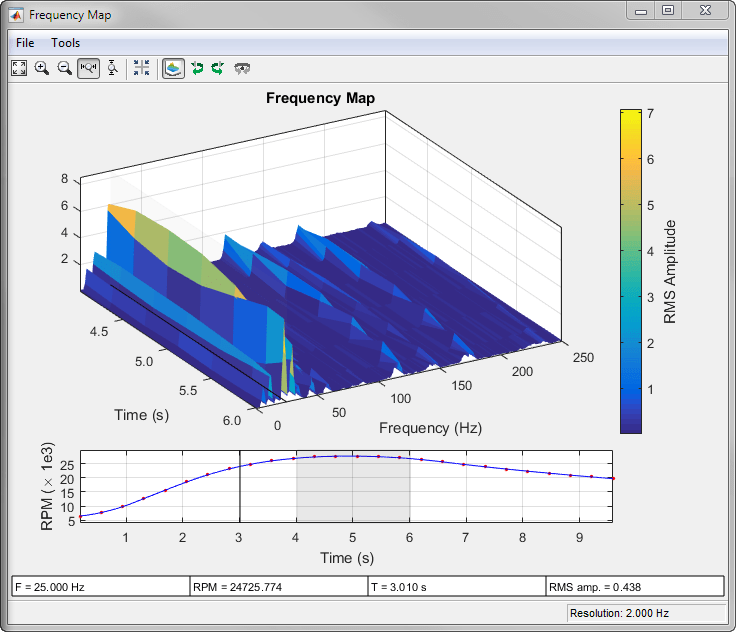
rpmfreqmap(___) with no output
arguments plots the frequency map as a function of rotational speed
and time on an interactive figure. The plot is also known as a Campbell
diagram.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
References
[1] Brandt, Anders. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures. Chichester, UK: John Wiley & Sons, 2011.
Extended Capabilities
Version History
Introduced in R2015bSee Also
orderspectrum | ordertrack | orderwaveform | rpmordermap | rpmtrack | spectrogram | tachorpm