Amplifier
Model amplifier in RF systems
Libraries:
RF Blockset /
Circuit Envelope /
Elements
Description
Use the Amplifier block to model a linear or
nonlinear amplifier, with or without noise. Defining the amplifier
gain using a data source also defines input data visualization and
modeling. Use the Main tab parameters to specify
amplifier gain and noise using data sheet values, standard s2p files,
S-parameters, or circuit envelope polynomial coefficients.
The amplifier is implemented as a polynomial, voltage-controlled voltage source (VCVS) except
when the amplifier gain is obtained from a Data source. The
VCVS includes nonlinearities that are described using parameters listed in the
Nonlinearity tab. To model linear amplification, the amplifier
implements the relation Vout =
a1*Vin between the input and output voltages. The input voltage is Vi(t) =
Ai(t)ejωt, and the output voltage is Vo(t) =
Ao(t)ejωt at each carrier w = 2πf in the RF Blockset™ environment.
In case the amplifier gain is obtained from a data source, amplifier implementation is based on S-parameter data. Nonlinear amplification is modeled as a polynomial (with the saturation power computed automatically). It also produces additional intermodulation frequencies.
Amplifier block mask icons are dynamic and show the current state of the applied noise parameter. This table shows you how the icons on this block vary based on the state of the Noise figure (dB) parameter on the block.
Noise Figure (dB): 10 | Noise Figure (dB): 0 |
|---|---|
|
|
|
Examples
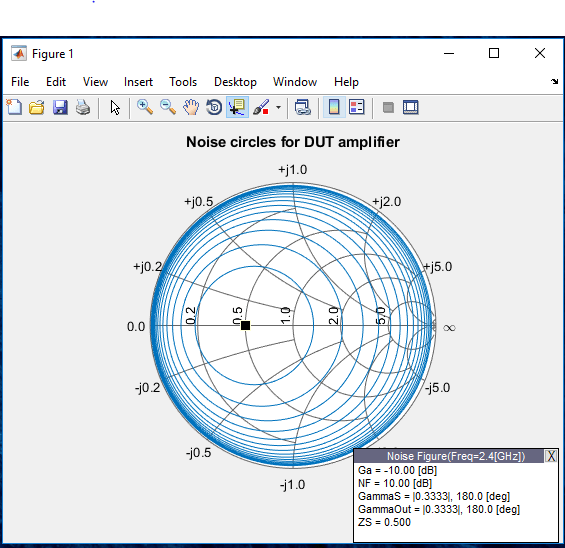
Spot Noise Data in Amplifiers and Effects on Measured Noise Figure
A test bench model to describe the noise introduced by a 2-port device.
Validating IP2/IP3 Using Complex Signals
Run a two-tone experiment to measure the second- and third-order intercept points of an amplifier.
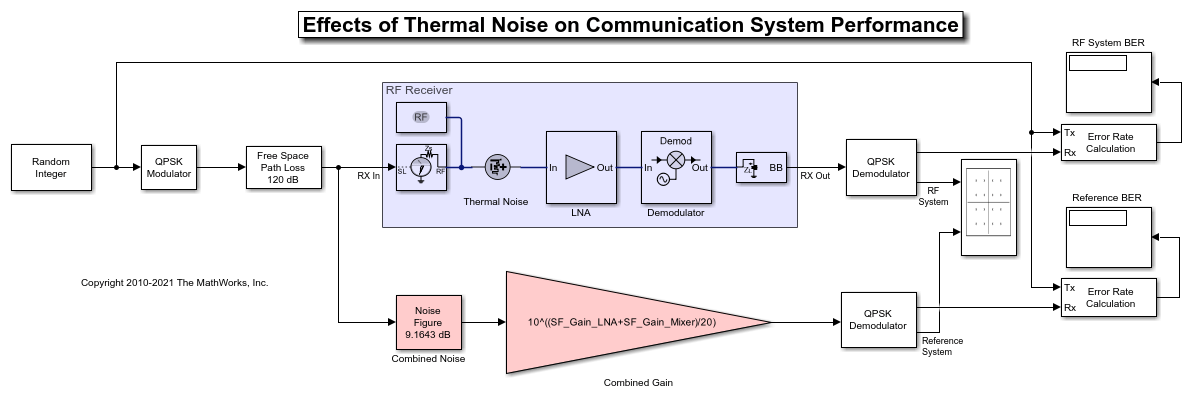
Impact of Thermal Noise on Communication System Performance
Model thermal noise in a super-heterodyne RF receiver and measure its effects on a communications system noise figure and bit error rate.
Executable Specification of Direct Conversion Receiver
Simulate the sensitivity performance of a direct conversion architecture with the following RF impairments.
Parameters
Main
Source of the amplifier gain, specified as one of the following:
Available power gain— The block uses the Available power gain parameter to calculate a1, the linear voltage gain term of the polynomial VCVS. This calculation assumes a matched load termination for the amplifier.Open circuit voltage gain— The block uses the Open circuit voltage gain parameter to calculate a1, the linear voltage gain term of the polynomial VCVS.Data source— The block uses the Data source parameter to calculate the linear voltage gain. When you use the data source option, the block uses S11 and S22 as the input and output impedances.Polynomial coefficients— The block uses the Polynomial coefficients parameter to calculate the nonlinear voltage gain.AM/AM-AM/PM table— The block uses the AM/AM-AM/PM table parameter to determine the power characteristics of the amplifier.
Available power gain of amplifier, specified as a scalar in dB. Specify the units from the corresponding drop-down list.
Dependencies
To enable this parameter, choose Available power
gain in the Source of amplifier
gain tab.
Open circuit voltage of amplifier, specified as a scalar in dB. Specify the units from the corresponding drop-down list.
Dependencies
To enable this parameter, choose Open circuit voltage
gain in the Source of amplifier
gain tab.
Data source, specified as one of the following:
Data file— Name of a Touchstone file with the extension.s2p.Network-parameters— Provide Network parameter data such asS-parameters,Y-parameters, andZ-parameterswith corresponding Frequency and Reference impedance (ohms) for the amplifier.Rational model— Provide values for Residues, Poles, and Direct feedthrough parameters which correspond to the equation for a rational modelIn this rational model equation, each Ck is the residue of the pole Ak. If Ck is complex, a corresponding complex conjugate pole and residue must also be enumerated. This object has the properties
C,A, andD. You can use these properties to specify the Residues, Poles, and Direct feedthrough parameters.
When the amplifier is nonlinear, the nonlinearity applies only to the S21 term of the scattering parameters representing the 2-port element. In this case, S21 is frequency-independent with its constant value being either the maximal value of S21, or the S21 value at an Operation frequency specified by the user. The other scattering parameters, S11, S12, and S22 remain the same as in the linear case.
Dependencies
To enable this parameter, select Data
source in Source of amplifier
gain tab.
Order of polynomial, specified as a vector.
The order of the polynomial must be less than or equal to 9. The
coefficients are ordered in ascending powers. If a vector has 10
coefficients,
[,
the polynomial it represents is:a0,a1,a2,
... a9]
Vout = a0 + a1Vin + a2Vin2 + ...
+ a9Vin9
where
a1 represents the linear
gain term, and higher-order terms are modeled according to [1].
For example, the vector
[
specifies the relation Vout = a0 + a1V1 + a2V12 + a3V13. Trailing zeroes are omitted. So,
a0,a1,a2,a3][
defines the same polynomial as
a0,a1,a2][. The default value of this parameter is [0,1],
corresponding to the linear relation
Vout =
Vin.a0,a1,a2,
0]
Dependencies
To enable this parameter, select Polynomial
coefficients in Source of amplifier
gain tab.
Table lookup entries specified as a real M-by-3 matrix. The second column of the matrix represents the AM/AM–AM/PM model output power in dBm. The third column represents the model phase change in degrees. The second and third column values are related to the absolute value of the power of the input signal represented in the first column of matrix. The input power in the first column must increase monotonically.
Dependencies
To enable this parameter, set Source of amplifier
gain to AM/AM - AM/PM
table.
Select this parameter to use a network parameter object as the source of amplifier gain.
Once you select this parameter, in the text box that opens, specify one of these:
Network parameter object.
MATLAB® base workspace variable or a Simulink® model workspace variable. The block evaluates if the specified variable is a network parameter object.
The network parameter objects that you can specify include:
Dependencies
To enable this parameter, first select Data
source in Source of amplifier
gain, and then select
Network-parameters in Data
source.
Network parameter type, specified as S-parameters,
Y-parameters, or
Z-parameters.
Dependencies
To enable this parameter, first select Data
source in Source of amplifier
gain and then, select
Network-parameters in the
Data source.
Input impedance of amplifier, specified as a positive scalar in ohms.
Dependencies
To enable this parameter, select Available power
gain, Open circuit voltage
gain, or Polynomial
coefficients in Source of amplifier
gain.
Output impedance of amplifier, specified as a positive scalar in ohms.
Dependencies
To enable this parameter, select Available power
gain, Open circuit voltage
gain, or Polynomial
coefficients in Source of amplifier
gain.
Name of network parameter data file, specified as a character vector.
Dependencies
To enable this parameter, first select Data
source in Source of amplifier
gain and then, select Data
file in Data source.
Frequency of network parameters, specified as a scalar in Hz.
Dependencies
To enable this parameter, first select Data
source in Source of amplifier
gain and then, select
Network-parameters in Data
source.
Reference impedance of network parameters, specified as a positive scalar or vector of positive scalars in ohms.
Note
The reference impedance of all the ports must be equal when you specify it as a vector of positive scalars.
Dependencies
To enable this parameter, first select Data
source in Source of amplifier
gain and then, select
Network-parameters in Data
source.
Select this parameter to use a rational object as the
data source to model amplifier gain.
Once you select this parameter, in the text box that opens, specify one of these:
rationalobject.MATLAB base workspace variable or a Simulink model workspace variable. The block evaluates if the specified variable is a rational object."
The rational objects that you can specify include:
Dependencies
To enable this parameter, first select Data
source in Source of amplifier
gain, and then select Rational
model in Data source.
Residues in order of rational model, specified as a vector.
Dependencies
To enable this parameter, first select Data
source in Source of amplifier
gain and then, select Rational
model in Data source.
Poles in order of rational model, specified as a vector.
Dependencies
To enable this parameter, first select Data
source in Source of amplifier
gain and then, select Rational
model in Data source.
Direct feedthrough, specified as an array vector.
Dependencies
To enable this parameter, first select Data
source in Source of amplifier
gain and then, select Rational
model in Data source.
Select this option to ground and hide the negative terminals. Clear this parameter to expose the negative terminals. By exposing these terminals, you can connect them to other parts of your model.
By default, this option is selected.
Nonlinearity
Type of nonlinearity, specified as Even and odd
order or Odd order.
When you select
Even and odd order, the amplifier can produce second- and third-order intermodulation frequencies in addition to a linear term.When you select
Odd order, the amplifier generates only odd order intermodulation frequencies.The linear gain determines the linear a1 term. The block calculates the remaining terms from the specified parameters. These parameters are IP3, 1-dB gain compression power, Output saturation power, and Gain compression at saturation. The number of constraints you specify determines the order of the model. The figure shows the graphical definition of the nonlinear amplifier parameters.

Intercept points convention, specified a
Input-referred, or
Output-referred convention. Use this
specification for the intercept points, 1-dB gain compression power, and
saturation power.
Second-order intercept point, specified as a scalar.
Dependencies
To set this parameter, select Even and odd
order in Nonlinear polynomial
type.
Third-order intercept point, specified as a scalar.
1-dB gain compression power, specified as a scalar.
Dependencies
To set this parameter, select Odd order
in Nonlinear polynomial type.
Output saturation power, specified as scalar. The block uses this value to calculate the voltage saturation point used in the nonlinear model. In this case, the first derivative of the polynomial is zero, and the second derivative is negative.
Dependencies
To set this parameter, select Odd order
in Nonlinear polynomial type.
Gain compression at saturation, specified as scalar.
When Nonlinear polynomial type is
Odd order, specify the gain compression
at saturation.
Dependencies
To set this parameter, first select Odd
order in Nonlinear polynomial
type. Then, change the default value of
Output saturation power.
Select this parameter to specify operation frequency at the maximum magnitude of S21.
Dependencies
To enable this parameter:
First, choose
Data sourcein the Source of amplifier gain parameter on theMain tab.Second, specify the nonlinearity in the Nonlinearity tab.
And finally, click the Apply button.
Operation frequency, specified as a scalar or finite vector.
Dependencies
To enable this parameter:
First, choose
Data sourcein the Source of amplifier gain parameter on theMain tab.Second, specify the nonlinearity in the Nonlinearity tab.
And finally, click the Apply button.
Note
If the Use constant S21 and nonlinearity parameter is selected, clear this parameter to enable the Operation frequency parameter.
Select this parameter to use the constant magnitude of S21 and nonlinearity in your amplifier model.
Dependencies
To enable this parameter:
First, choose
Data sourcein the Source of amplifier gain parameter on theMain tab.Second, specify the nonlinearity in the Nonlinearity tab.
And finally, click the Apply button.
Use this button to plot the power characteristics of the amplifier based on the nonlinearity parameters specified on the Nonlinearity tab. When you clear the Use constant S21 and nonlinearity parameter, the power curve reflects the amplifier power measured at the frequency specified in the Operation frequency parameter.
Dependencies
To enable this parameter, set Source of amplifier
gain in the Main tab to
Available power gain,
Open circuit voltage gain, or
Data source.
Noise
Select this parameter, to simulate noise as specified in block parameters or on file.
If the noise is specified in an .s2p file, then it
is used for simulation.
Noise type, specified as Noise figure or
Spot noise data.
Noise distribution, specified as:
White, spectral density is a single non-negative value. The power value of the noise depends on the bandwidth of the carrier and the bandwidth depends on the time step. This is an uncorrelated noise source.Piece-wise linear, spectral density is a vector of values [pi]. For each carrier, the noise source behaves like a white uncorrelated noise. The power of the noise source is carrier-dependent.Colored, depends on both carrier and bandwidth. This is a correlated noise source.
Noise figure, specified as a scalar in decibels.
Frequency data, specified as a real scalar or finite vector in Hz, kHz, MHz, or GHz.
Dependencies
To set this parameter, first select Piece-wise
linear or Colored in
Noise distribution.
Minimum noise figure, specified as a scalar or finite vector in decibels.
Dependencies
To set this parameter, first select Spot noise
data in Noise type.
Optimal reflection coefficient, specified as a scalar or a finite vector.
Dependencies
To set this parameter, first select Spot noise
data in Noise type.
Equivalent normalized noise resistance, specified as a scalar or finite vector.
Dependencies
To set this parameter, first select Spot noise
data in Noise type.
Select this parameter to automatically calculate impulse response for frequency dependent noises. Clear this parameter to manually specify the impulse response duration using Impulse response duration. You cannot specify impulse response when amplifier is nonlinear, as in this case noise is simulated as white-noise.
Dependencies
To set this parameter, first select
Colored in Noise
distribution.
Impulse response duration used to simulate frequency dependent noise, specified as a scalar in seconds. You cannot specify impulse response if the amplifier is nonlinear.
Dependencies
To set this parameter, first clear Automatically estimate impulse response duration.
Modeling
Model S-parameters, specified as:
Time domaintechnique creates an analytical rational model that approximates the whole range of the data. When modeling usingTime domain, the Plot inVisualizationtab plots the data defined inData Sourceand the values in therationalfitfunction.Frequency domaincomputes the baseband impulse response for each carrier frequency independently. This technique is based on convolution. There is an option to specify the duration of the impulse response. For more information, see Compare Time and Frequency Domain Simulation Options for S-parameters.For the Amplifier, Antenna, and S-Parameters blocks, the default value is
Time domain. For the Transmission Line block, the default value isFrequency domain.
Dependencies
To set this parameter, first select Data
source in Source of amplifier
gain. This selection activates the
Modeling Tab which contains
Modeling options
Rationalfit fitting options, specified as Fit
individually, Share poles by
column, or Share all
poles.
Rational fitting results shows values of Number of independent fits, Number of required poles, and Relative error achieved (dB).
Dependencies
To set this parameter, select Time
domain in Modeling options.
Relative error acceptable for the rational fit, specified as a scalar in decibels.
Dependencies
To set this parameter, select Time
domain in Modeling options.
Select this parameter to automatically calculate impulse response. Clear this parameter to manually specify the impulse response duration using Impulse response duration.
Dependencies
To set this parameter, select Frequency
domain in Modeling options.
Impulse response duration, specified as a scalar in seconds.
Dependencies
To set this parameter, first select Frequency
domain in Modeling options.
Then, clear Automatically estimate impulse response
duration.
Select this parameter to S-parameter phase and delay the impulse response by half its length. This parameter is applicable only for S-parameter data modeled in time domain. You can use this parameter to shape spectral content with filter effects by specifying only magnitude.
Note
This parameter introduces an artificial delay to the system.
Visualization
Frequency data source, specified as:
When Source of frequency data is
Extracted from data source, the
Data source must be set to Data
file. Verify that the specified Data
file contains frequency data.
When Source of frequency data is
User-specified, specify a vector of
frequencies in the Frequency data parameter. Also,
specify units from the corresponding drop-down list.
Dependencies
To set this parameter, first select Data
source in Source of amplifier
gain. This selection activates the
Visualization Tab which contains
Source of frequency data
Frequency data range, specified as a finite vector.
Dependencies
To enable this parameter, set Source of frequency
data to
User-specified.
Type of data plot that you want to produce with your data specified as one of the following:
X-Y plane— Generate a Cartesian plot of your data versus frequency. To create linear, semilog, or log-log plots, set the Y-axis scale and X-axis scale accordingly.Polar plane— Generate a polar plot of your data. The block plots only the range of data corresponding to the specified frequencies.Z smith chart,Y smith chart, andZY smith chart— Generate a Smith® chart. The block plots only the range of data corresponding to the specified frequencies.
Type of S-Parameters to plot, specified as S11,
S12, S21, or
S22. When noise is spectral NF
plotting is possible.
Dependencies
To enable NF, set Noise
type to Noise figure and
select Apply.
Type of S-Parameters to plot, specified as S11,
S12, S21, or
S22. When noise is spectral NF
plotting is possible.
Dependencies
To enable NF, set Noise
distribution to Piece-wise
linear or Colored and
select Apply.
Plot format, specified as Magnitude (decibels),
Angle(degrees), Real, or
Imaginary.
Dependencies
To enable this parameter, set Plot type to
X-Y plane.
Plot format, specified as Magnitude (decibels),
Angle(degrees), Real, or
Imaginary.
Dependencies
To enable this parameter, set Plot type to
X-Y plane.
Y-axis scale, specified as Linear or
Logarithmic.
Dependencies
To enable this parameter, set Plot type to
X-Y plane.
X-axis scale, specified as Linear or
Logarithmic.
Dependencies
To enable this parameter, set Plot type to
X-Y plane.
Plot specified data using plot button.
More About
Noise figure represents only a subset of the noise information (spot noise data) needed to fully describe the noise behavior of a two-port device. When only noise figure is specified, RF Blockset amplifier defines the spot noise parameters in the following manner:
Amplifier exhibits specified noise figure when source impedance is matched to the reference impedance ().
Noise in RF Blockset amplifiers are represented as two correlated noise sources at the input port of a noiseless two-port:
The noise sources variance and correlation are governed by an ABCD-correlation matrix:
that is determined by measurable quantities:
NFmin - Minimum noise figure
Rn - Equivalent noise resistance
Yopt - Optimal source admittance
k - Boltzman's constant
T - Noise temperature in Kelvin
.
The above quantities are specified in the amplifier from the noise data section in
the .s2p file or directly as masked parameters in the noise pane.
In both cases:
NFmin is specified in decibels
Rn is specified as equivalent normalized resistance, RN (
Rn = Z0RN).Yopt is specified in terms of optimal reflection coefficient, Γopt (
Yopt = Y0(1-Γopt)/(1+Γopt)).
In the above, Z0 =
1/Y0 is the reference impedance that is
real. If the Source of amplifier gain is Data
source, the reference impedance is specified in the
.s2p file or in the amplifier mask. Other wise the reference
impedance is 50 ohms.
The noise factor, F, of the amplifier is affected by the noisy source impedance, Zs, and is determined from the ABCD-correlation matrix:
The noise figure, NF, is obtained from the noise factor using, NF =
10log(F).
References
[1] Gonzalez, Guillermo. “Microwave Transistor Amplifiers: Analysis and Design”, Englewood Cliffs, N.J.: Prentice-Hall, 1984.
[2] Kundert, Ken. “Accurate and Rapid Measurement of IP 2 and IP 3”, The Designers Guide Community, Version 1b, May 22, 2002. http://www.designers-guide.org/analysis/intercept-point.pdf.
[3] Pozar, David M. “Microwave Engineering”, Hoboken NJ: John Wiley & Sons, 2005.
[4] Razavi, Behzad. RF Microelectronics. Upper Saddle River, NJ: Prentice Hall, 2011.
Version History
Introduced in R2010bThe Amplifier block now supports the improved polynomial model to compute nonlinearity that better adheres to user specification.
When you open a model created before R2025a containing the Amplifier block, the software uses the improved polynomial model to compute nonlinearity and numerical results may be different.
The Time domain (rationalfit) parameter value in the
Modeling options parameter has been renamed to
Time domain in the Amplifier
block.
When you open a model created before R2024b containing an Amplifier
block, the parameter name displays as Time domain.
The Amplifier block has three new parameters.
Network-parameter object — Use this parameter to specify a network parameter object as the source of amplifier gain.
Use rational object — Use this parameter to specify a
rationalobject as the source of amplifier gain.Plot power characteristics — Use this button to plot the power characteristics of an amplifier based on the specified nonlinearities.
The Pick operation frequency at maximum S21 magnitude and Frequency data parameters have been renamed to Use operation frequency at maximum S21 magnitude and Source of frequency data, respectively.
When you open a model created before R2022b containing the Amplifier block, the software replaces the old parameter names with the new names.
The Amplifier block now enables you to model frequency-dependent noise as colored noise when your amplifier operates in a nonlinear region.
When you open a model created before R2022a containing the Amplifier block operating in a nonlinear region with frequency-dependent noise, the software models the noise as specified in the block.
The Amplifier block has two new parameters.
AM/AM-AM/PM table — Use this parameter to specify amplifier power characteristics using AM/AM-AM/PM table.
Use constant S21 and nonlinearity — Use this parameter to model frequency-dependent gain (S21) when operating in a nonlinear region.
Starting in R2021b, the Amplifier block icon has updated. The block icon is now dynamic and shows the current state of the noise parameter.
When you open a model created before R2021b containing an Amplifier block, the software replaces the block icon with the R2021b version.
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)