GapEvaluation

Gap criterion clustering evaluation object

expand all in page

    Description

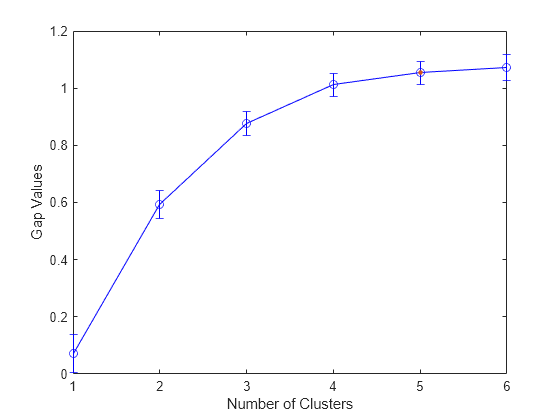
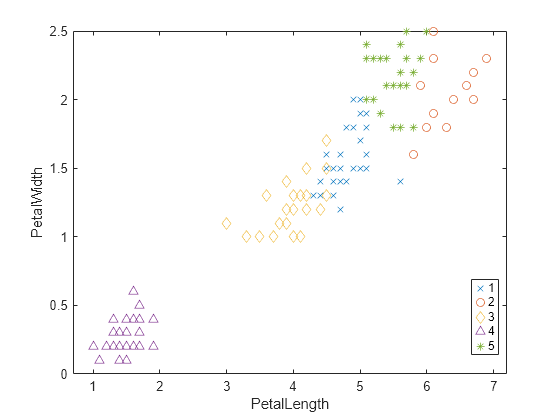
    GapEvaluation is an object consisting of sample data (X), clustering data (OptimalY), and gap criterion values (CriterionValues) used to evaluate the optimal number of clusters (OptimalK). The gap criterion values correspond to the difference ExpectedLogW – LogW, where W is the within-cluster dispersion, ExpectedLogW is determined by Monte Carlo sampling from a reference distribution, and LogW is computed from the sample data. The optimal number of clusters corresponds to the solution with the largest local or global gap value within a tolerance range (SearchMethod). For more information, see Gap Value.

    Creation

    Create a gap criterion clustering evaluation object by using the evalclusters function and specifying the criterion as "gap".

    You can then use compact to create a compact version of the gap criterion clustering evaluation object. The function removes the contents of the properties X, OptimalY, and Missing.

    Properties

    expand all

    Clustering Evaluation Properties

    This property is read-only.

    Clustering algorithm used to cluster the sample data, returned as 'kmeans', 'linkage', 'gmdistribution', or a function handle.

    ValueDescription
    'kmeans'Cluster the data in X using the kmeans clustering algorithm, with EmptyAction set to "singleton" and Replicates set to 5.
    'linkage'Cluster the data in X using the clusterdata agglomerative clustering algorithm, with Linkage set to "ward".
    'gmdistribution'Cluster the data in X using the gmdistribution Gaussian mixture distribution algorithm, with SharedCov set to true and Replicates set to 5.

    Data Types: char | function_handle

    This property is read-only.

    Name of the criterion used for clustering evaluation, returned as 'Gap'.

    This property is read-only.

    Criterion values, returned as a numeric vector. Each value corresponds to a proposed number of clusters in InspectedK.

    Data Types: double

    This property is read-only.

    Distance metric used for clustering data and computing the criterion values, returned as one of the values in this table or a function handle.

    ValueDescription
    'sqEuclidean'Squared Euclidean distance
    'Euclidean'Euclidean distance
    'cityblock'Sum of absolute differences
    'cosine'One minus the cosine of the included angle between points (treated as vectors)
    'correlation'One minus the sample correlation between points (treated as sequences of values)

    Data Types: char | function_handle

    This property is read-only.

    List of the number of proposed clusters for which to compute criterion values, returned as a positive integer vector.

    Data Types: double

    This property is read-only.

    Optimal number of clusters, returned as a positive integer scalar.

    Data Types: double

    This property is read-only.

    Optimal clustering solution corresponding to OptimalK, returned as a positive integer column vector. Each row of OptimalY represents the cluster index of the corresponding observation (or row) in X. If you specify the clustering solutions as an input argument to evalclusters when you create the clustering evaluation object, or if the clustering evaluation object is compact (see compact), then OptimalY is empty.

    Data Types: double

    This property is read-only.

    Method for selecting the optimal number of clusters, returned as 'globalMaxSE' or 'firstMaxSE'.

    ValueDescription
    'globalMaxSE'

    Evaluate each proposed number of clusters in InspectedK and select the smallest number of clusters satisfying

    Gap(K)≥GAPMAX−SE(GAPMAX),

    where K is the number of clusters, Gap(K) is the gap value for the clustering solution with K clusters, GAPMAX is the largest gap value, and SE(GAPMAX) is the standard error corresponding to the largest gap value.

    'firstMaxSE'

    Evaluate each proposed number of clusters in InspectedK and select the smallest number of clusters satisfying

    Gap(K)≥Gap(K+1)−SE(K+1),

    where K is the number of clusters, Gap(K) is the gap value for the clustering solution with K clusters, and SE(K + 1) is the standard error of the clustering solution with K + 1 clusters.

    Sample Data Properties

    This property is read-only.

    Natural logarithm of the within-cluster dispersion W based on the sample data X, returned as a numeric vector. W is the within-cluster dispersion computed using the distance metric Distance. Each element of LogW corresponds to a specific number of proposed clusters (an element of InspectedK).

    Data Types: double

    This property is read-only.

    Excluded data, returned as a logical column vector. If an element of Missing is true, then the corresponding observation (or row) in the data matrix X is not used in the clustering solutions. If the clustering evaluation object is compact (see compact), then Missing is empty.

    Data Types: double | logical

    This property is read-only.

    Number of observations in the data matrix X, ignoring observations with missing (NaN) values, returned as a positive integer scalar.

    Data Types: double

    This property is read-only.

    Data used for clustering, returned as a numeric matrix. Rows correspond to observations, and columns correspond to variables. If the clustering evaluation object is compact (see compact), then X is empty.

    Data Types: single | double

    Reference Data Properties

    This property is read-only.

    Number of reference data sets generated from the reference distribution ReferenceDistribution, returned as a positive integer scalar.

    Data Types: double

    This property is read-only.

    Expectation of the natural logarithm of the within-cluster dispersion W based on the generated reference data, returned as a numeric vector. W is the within-cluster dispersion computed using the distance metric Distance. Each element of ExpectedLogW corresponds to a specific number of proposed clusters (an element of InspectedK).

    Data Types: double

    This property is read-only.

    Reference data generation method, returned as 'PCA' or 'uniform'.

    ValueDescription
    'PCA'Generate reference data from a uniform distribution over a box aligned with the principal components of the data matrix X.
    'uniform'Generate reference data uniformly over the range of each feature in the data matrix X.

    This property is read-only.

    Standard error of the natural logarithm of the within-cluster dispersion W with respect to the reference data, returned as a numeric vector. W is the within-cluster dispersion computed using the distance metric Distance. Each element of SE corresponds to a specific number of proposed clusters (an element of InspectedK).

    Data Types: double

    This property is read-only.

    Standard deviation of the natural logarithm of the within-cluster dispersion W with respect to the reference data, returned as a numeric vector. W is the within-cluster dispersion computed using the distance metric Distance. Each element of StdLogW corresponds to a specific number of proposed clusters (an element of InspectedK).

    Data Types: double

    Object Functions

    addKEvaluate additional numbers of clusters
    compactCompact clustering evaluation object
    increaseBIncrease reference data sets
    plot Plot clustering evaluation object criterion values

    Examples

    collapse all

    Open Live Script

    Evaluate the optimal number of clusters using the gap clustering evaluation criterion.

    Load the fisheriris data set. The data contains length and width measurements from the sepals and petals of three species of iris flowers.

    load fisheriris

    Evaluate the optimal number of clusters based on the gap criterion values. Cluster the data using kmeans.

    rng("default") % For reproducibility
evaluation = evalclusters(meas,"kmeans","gap","KList",1:6)
    evaluation = 
  GapEvaluation with properties:

    NumObservations: 150
         InspectedK: [1 2 3 4 5 6]
    CriterionValues: [0.0720 0.5928 0.8762 1.0114 1.0534 1.0720]
           OptimalK: 5


  Properties, Methods

    The OptimalK value indicates that, based on the gap criterion, the optimal number of clusters is five.

    Plot the gap criterion values for each number of clusters tested.

    plot(evaluation)

    Figure contains an axes object. The axes object with xlabel Number of Clusters, ylabel Gap Values contains 2 objects of type errorbar, line.

    Based on the plot, the maximum value of the gap criterion occurs at six clusters. However, the value at five clusters is within one standard error of the maximum, so the suggested optimal number of clusters is five.

    Create a grouped scatter plot to examine the relationship between petal length and width. Group the data by the suggested clusters.

    PetalLength = meas(:,3);
PetalWidth = meas(:,4);
clusters = evaluation.OptimalY;
gscatter(PetalLength,PetalWidth,clusters,[],"xod^*");

    Figure contains an axes object. The axes object with xlabel PetalLength, ylabel PetalWidth contains 5 objects of type line. One or more of the lines displays its values using only markers These objects represent 1, 2, 3, 4, 5.

    The plot shows cluster 4 in the lower-left corner, completely separated from the other four clusters. Cluster 4 contains flowers with the smallest petal widths and lengths. Cluster 2 is in the upper-right corner, and contains flowers with the largest petal widths and lengths. Cluster 5 is next to cluster 2, and contains flowers with similar petal widths but smaller petal lengths compared to the flowers in cluster 2. Clusters 1 and 3 are near the center of the plot, and contain flowers with measurements between the extremes.

    More About

    expand all

    References

    [1] Tibshirani, R., G. Walther, and T. Hastie. “Estimating the number of clusters in a data set via the gap statistic.” Journal of the Royal Statistical Society: Series B. Vol. 63, Part 2, 2001, pp. 411–423.

    Version History

    Introduced in R2013b

    See Also

    | | |