fitcdiscr

Fit discriminant analysis classifier

collapse all in page

Syntax

Mdl = fitcdiscr(Tbl,ResponseVarName)

Mdl = fitcdiscr(Tbl,formula)

Mdl = fitcdiscr(Tbl,Y)

Mdl = fitcdiscr(X,Y)

Mdl = fitcdiscr(___,Name=Value)

[Mdl,AggregateOptimizationResults] = fitcdiscr(___)

Description

Mdl = fitcdiscr(Tbl,ResponseVarName) returns a fitted discriminant analysis model based on the input variables (also known as predictors, features, or attributes) contained in the table Tbl and output (response or labels) contained in ResponseVarName.

Mdl = fitcdiscr(Tbl,formula) returns a fitted discriminant analysis model based on the input variables contained in the table Tbl. formula is an explanatory model of the response and a subset of predictor variables in Tbl used to fit Mdl.

Mdl = fitcdiscr(Tbl,Y) returns a fitted discriminant analysis model based on the input variables contained in the table Tbl and response Y.

Mdl = fitcdiscr(X,Y) returns a discriminant analysis classifier based on the input variables X and response Y.

example

Mdl = fitcdiscr(___,Name=Value) fits a classifier with additional options specified by one or more name-value arguments, using any of the previous syntaxes. For example, you can optimize hyperparameters to minimize the model’s cross-validation loss, or specify the cost of misclassification, the prior probabilities for each class, or the observation weights.

example

[Mdl,AggregateOptimizationResults] = fitcdiscr(___) also returns AggregateOptimizationResults, which contains hyperparameter optimization results when you specify the OptimizeHyperparameters and HyperparameterOptimizationOptions name-value arguments. You must also specify the ConstraintType and ConstraintBounds options of HyperparameterOptimizationOptions. You can use this syntax to optimize on compact model size instead of cross-validation loss, and to perform a set of multiple optimization problems that have the same options but different constraint bounds.

Note

For a list of supported syntaxes when the input variables are tall arrays, see Tall Arrays.

Examples

collapse all

Train Discriminant Analysis Model

Open Live Script

Load Fisher's iris data set.

load fisheriris

Train a discriminant analysis model using the entire data set.

Mdl = fitcdiscr(meas,species)

Mdl = 
  ClassificationDiscriminant
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: {'setosa'  'versicolor'  'virginica'}
           ScoreTransform: 'none'
          NumObservations: 150
              DiscrimType: 'linear'
                       Mu: [3x4 double]
                   Coeffs: [3x3 struct]

Mdl is a ClassificationDiscriminant model. To access its properties, use dot notation. For example, display the group means for each predictor.

Mdl.Mu

ans = 3×4

    5.0060    3.4280    1.4620    0.2460
    5.9360    2.7700    4.2600    1.3260
    6.5880    2.9740    5.5520    2.0260

To predict labels for new observations, pass Mdl and predictor data to predict.

Optimize Discriminant Analysis Model

Open Live Script

This example shows how to optimize hyperparameters automatically using fitcdiscr. The example uses Fisher's iris data.

Load the data.

load fisheriris

Find hyperparameters that minimize five-fold cross-validation loss by using automatic hyperparameter optimization.

For reproducibility, set the random seed and use the 'expected-improvement-plus' acquisition function.

rng(1)
Mdl = fitcdiscr(meas,species,'OptimizeHyperparameters','auto',...
    'HyperparameterOptimizationOptions',...
    struct('AcquisitionFunctionName','expected-improvement-plus'))

|=====================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |        Delta |        Gamma |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|    1 | Best   |     0.66667 |     0.44974 |     0.66667 |     0.66667 |       13.261 |      0.25218 |
|    2 | Best   |        0.02 |     0.10534 |        0.02 |    0.064227 |   2.7404e-05 |     0.073264 |
|    3 | Accept |        0.04 |    0.048045 |        0.02 |    0.020084 |   3.2455e-06 |      0.46974 |
|    4 | Accept |     0.66667 |    0.067324 |        0.02 |    0.020118 |       14.879 |      0.98622 |
|    5 | Accept |    0.046667 |    0.073803 |        0.02 |    0.019907 |   0.00031449 |      0.97362 |
|    6 | Accept |        0.04 |    0.053434 |        0.02 |    0.028438 |   4.5092e-05 |      0.43616 |
|    7 | Accept |    0.046667 |    0.053789 |        0.02 |    0.031424 |   2.0973e-05 |       0.9942 |
|    8 | Accept |        0.02 |    0.039878 |        0.02 |    0.022424 |   1.0554e-06 |    0.0024286 |
|    9 | Accept |        0.02 |    0.036023 |        0.02 |    0.021105 |   1.1232e-06 |   0.00014039 |
|   10 | Accept |        0.02 |    0.037404 |        0.02 |    0.020948 |   0.00011837 |    0.0032994 |
|   11 | Accept |        0.02 |    0.042595 |        0.02 |    0.020172 |   1.0292e-06 |     0.027725 |
|   12 | Accept |        0.02 |    0.041256 |        0.02 |    0.020105 |   9.7792e-05 |    0.0022817 |
|   13 | Accept |        0.02 |    0.046664 |        0.02 |    0.020038 |   0.00036014 |    0.0015136 |
|   14 | Accept |        0.02 |    0.037616 |        0.02 |    0.019597 |   0.00021059 |    0.0044789 |
|   15 | Accept |        0.02 |    0.034784 |        0.02 |    0.019461 |   1.1911e-05 |    0.0010135 |
|   16 | Accept |        0.02 |    0.056015 |        0.02 |     0.01993 |    0.0017896 |   0.00071115 |
|   17 | Accept |        0.02 |    0.050028 |        0.02 |    0.019551 |   0.00073745 |    0.0066899 |
|   18 | Accept |        0.02 |    0.056639 |        0.02 |    0.019776 |   0.00079304 |   0.00011509 |
|   19 | Accept |        0.02 |     0.04676 |        0.02 |    0.019678 |     0.007292 |    0.0007911 |
|   20 | Accept |    0.046667 |    0.035902 |        0.02 |    0.019785 |    0.0074408 |      0.99945 |
|=====================================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |        Delta |        Gamma |
|      | result |             | runtime     | (observed)  | (estim.)    |              |              |
|=====================================================================================================|
|   21 | Accept |        0.02 |    0.071029 |        0.02 |    0.019043 |    0.0036004 |    0.0024547 |
|   22 | Accept |        0.02 |    0.033304 |        0.02 |    0.019755 |   2.5238e-05 |    0.0015542 |
|   23 | Accept |        0.02 |     0.10813 |        0.02 |      0.0191 |   1.5478e-05 |    0.0026899 |
|   24 | Accept |        0.02 |     0.03873 |        0.02 |    0.019081 |    0.0040557 |   0.00046815 |
|   25 | Accept |        0.02 |    0.034153 |        0.02 |    0.019333 |    2.959e-05 |    0.0011358 |
|   26 | Accept |        0.02 |    0.034087 |        0.02 |    0.019369 |   2.3111e-06 |    0.0029205 |
|   27 | Accept |        0.02 |    0.035847 |        0.02 |    0.019455 |   3.8898e-05 |    0.0011665 |
|   28 | Accept |        0.02 |    0.067496 |        0.02 |    0.019449 |    0.0035925 |    0.0020278 |
|   29 | Accept |     0.66667 |     0.10668 |        0.02 |    0.019479 |       998.93 |     0.064276 |
|   30 | Accept |        0.02 |     0.11601 |        0.02 |     0.01947 |   8.1557e-06 |    0.0008004 |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 18.3187 seconds
Total objective function evaluation time: 2.0585

Best observed feasible point:
      Delta        Gamma  
    __________    ________

    2.7404e-05    0.073264

Observed objective function value = 0.02
Estimated objective function value = 0.022693
Function evaluation time = 0.10534

Best estimated feasible point (according to models):
      Delta         Gamma  
    __________    _________

    2.5238e-05    0.0015542

Estimated objective function value = 0.01947
Estimated function evaluation time = 0.047364

Figure contains an axes object. The axes object with title Min objective vs. Number of function evaluations, xlabel Function evaluations, ylabel Min objective contains 2 objects of type line. These objects represent Min observed objective, Estimated min objective.

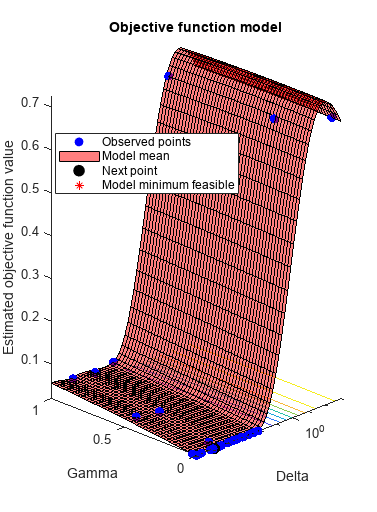
Figure contains an axes object. The axes object with title Objective function model, xlabel Delta, ylabel Gamma contains 5 objects of type line, surface, contour. One or more of the lines displays its values using only markers These objects represent Observed points, Model mean, Next point, Model minimum feasible.

Mdl = 
  ClassificationDiscriminant
                         ResponseName: 'Y'
                CategoricalPredictors: []
                           ClassNames: {'setosa'  'versicolor'  'virginica'}
                       ScoreTransform: 'none'
                      NumObservations: 150
    HyperparameterOptimizationResults: [1x1 BayesianOptimization]
                          DiscrimType: 'linear'
                                   Mu: [3x4 double]
                               Coeffs: [3x3 struct]

The fit achieves about 2% loss for the default 5-fold cross validation.

Optimize Discriminant Analysis Model on Tall Array

This example uses:

Open Live Script

This example shows how to optimize hyperparameters of a discriminant analysis model automatically using a tall array. The sample data set airlinesmall.csv is a large data set that contains a tabular file of airline flight data. This example creates a tall table containing the data and uses it to run the optimization procedure.

When you perform calculations on tall arrays, MATLAB® uses either a parallel pool (default if you have Parallel Computing Toolbox™) or the local MATLAB session. If you want to run the example using the local MATLAB session when you have Parallel Computing Toolbox, you can change the global execution environment by using the mapreducer function.

Create a datastore that references the folder location with the data. Select a subset of the variables to work with, and treat NA values as missing data so that datastore replaces them with NaN values. Create a tall table that contains the data in the datastore.

ds = datastore("airlinesmall.csv");
ds.SelectedVariableNames = ["Month","DayofMonth","DayOfWeek", ...
                            "DepTime","ArrDelay","Distance","DepDelay"];
ds.TreatAsMissing = "NA";
tt  = tall(ds) % Tall table

Starting parallel pool (parpool) using the 'Processes' profile ...
07-Dec-2023 09:05:49: Job Queued. Waiting for parallel pool job with ID 1 to start ...
07-Dec-2023 09:06:50: Job Queued. Waiting for parallel pool job with ID 1 to start ...
Connected to parallel pool with 6 workers.

tt =

  M×7 tall table

    Month    DayofMonth    DayOfWeek    DepTime    ArrDelay    Distance    DepDelay
    _____    __________    _________    _______    ________    ________    ________

     10          21            3          642          8         308          12   
     10          26            1         1021          8         296           1   
     10          23            5         2055         21         480          20   
     10          23            5         1332         13         296          12   
     10          22            4          629          4         373          -1   
     10          28            3         1446         59         308          63   
     10           8            4          928          3         447          -2   
     10          10            6          859         11         954          -1   
      :          :             :           :          :           :           :
      :          :             :           :          :           :           :

Determine the flights that are late by 10 minutes or more by defining a logical variable that is true for a late flight. This variable contains the class labels. A preview of this variable includes the first few rows.

Y = tt.DepDelay > 10 % Class labels

Y =

  M×1 tall logical array

   1
   0
   1
   1
   0
   1
   0
   0
   :
   :

Create a tall array for the predictor data.

X = tt{:,1:end-1} % Predictor data

X =

  M×6 tall double matrix

          10          21           3         642           8         308
          10          26           1        1021           8         296
          10          23           5        2055          21         480
          10          23           5        1332          13         296
          10          22           4         629           4         373
          10          28           3        1446          59         308
          10           8           4         928           3         447
          10          10           6         859          11         954
          :           :            :          :           :           :
          :           :            :          :           :           :

Remove rows in X and Y that contain missing data.

R = rmmissing([X Y]); % Data with missing entries removed
X = R(:,1:end-1); 
Y = R(:,end);

Standardize the predictor variables.

Z = zscore(X);

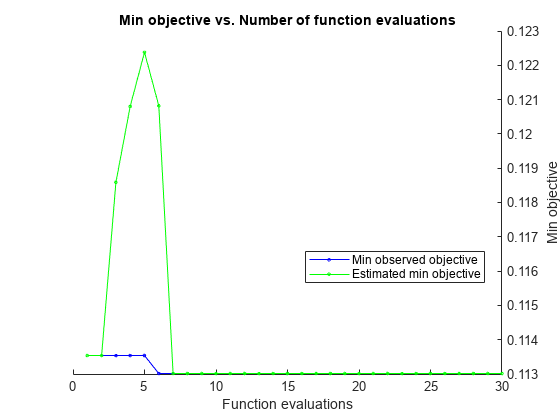
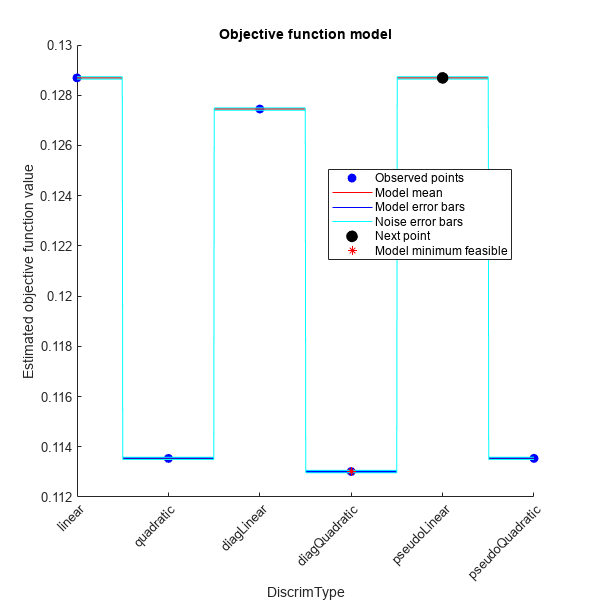
Optimize hyperparameters automatically using the OptimizeHyperparameters name-value argument. Note that when you use tall arrays, DiscrimType is the only hyperparameter you can optimize, regardless of whether you specify "auto" or "all". Find the optimal DiscrimType value that minimizes holdout cross-validation loss. For reproducibility, use the "expected-improvement-plus" acquisition function and set the seeds of the random number generators using rng and tallrng. The results can vary depending on the number of workers and the execution environment for the tall arrays. For details, see Control Where Your Code Runs.

rng("default") 
tallrng("default")
[Mdl,FitInfo,HyperparameterOptimizationResults] = fitcdiscr(Z,Y, ...
    "OptimizeHyperparameters","auto", ...
    "HyperparameterOptimizationOptions",struct("Holdout",0.3, ...
    "AcquisitionFunctionName","expected-improvement-plus"))

Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 2: Completed in 7.3 sec
- Pass 2 of 2: Completed in 3.8 sec
Evaluation completed in 19 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 4 sec
Evaluation completed in 4.3 sec
|======================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |  DiscrimType |
|      | result |             | runtime     | (observed)  | (estim.)    |              |
|======================================================================================|
|    1 | Best   |     0.11354 |      27.449 |     0.11354 |     0.11354 |    quadratic |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.3 sec
Evaluation completed in 2.5 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.2 sec
|    2 | Accept |     0.11354 |      5.4566 |     0.11354 |     0.11354 | pseudoQuadra |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.96 sec
Evaluation completed in 2.2 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.89 sec
Evaluation completed in 1.1 sec
|    3 | Accept |     0.12869 |      4.8549 |     0.11354 |     0.11859 | pseudoLinear |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.99 sec
Evaluation completed in 1.9 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.89 sec
Evaluation completed in 1.1 sec
|    4 | Accept |     0.12745 |      4.2867 |     0.11354 |      0.1208 |   diagLinear |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.98 sec
Evaluation completed in 2 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.84 sec
Evaluation completed in 1 sec
|    5 | Accept |     0.12869 |      4.6497 |     0.11354 |     0.12238 |       linear |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.7 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.89 sec
Evaluation completed in 1.1 sec
|    6 | Best   |     0.11301 |      4.0594 |     0.11301 |     0.12082 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.96 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.82 sec
Evaluation completed in 1 sec
|    7 | Accept |     0.11301 |      4.0419 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.85 sec
Evaluation completed in 1 sec
|    8 | Accept |     0.11301 |      4.0382 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.97 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.81 sec
Evaluation completed in 1 sec
|    9 | Accept |     0.11301 |      3.9186 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.9 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.84 sec
Evaluation completed in 1 sec
|   10 | Accept |     0.11301 |      4.0947 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.9 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.88 sec
Evaluation completed in 1.1 sec
|   11 | Accept |     0.11301 |      4.3088 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.94 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.8 sec
Evaluation completed in 1 sec
|   12 | Accept |     0.11301 |      3.9644 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 1.1 sec
|   13 | Accept |     0.11301 |      4.0673 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.93 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.94 sec
Evaluation completed in 1.2 sec
|   14 | Accept |     0.11301 |      4.1285 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.2 sec
Evaluation completed in 2 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.93 sec
Evaluation completed in 1.1 sec
|   15 | Accept |     0.11301 |      4.4217 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.98 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.89 sec
Evaluation completed in 1.1 sec
|   16 | Accept |     0.11301 |      4.0631 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.99 sec
Evaluation completed in 1.7 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 1.1 sec
|   17 | Accept |     0.11301 |      4.0227 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.9 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.88 sec
Evaluation completed in 1.1 sec
|   18 | Accept |     0.11354 |      4.3391 |     0.11301 |     0.11301 | pseudoQuadra |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.98 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.85 sec
Evaluation completed in 1 sec
|   19 | Accept |     0.11301 |       4.139 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.97 sec
Evaluation completed in 1.9 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.91 sec
Evaluation completed in 1.1 sec
|   20 | Accept |     0.11301 |      4.2078 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.9 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 1.1 sec
|======================================================================================|
| Iter | Eval   | Objective   | Objective   | BestSoFar   | BestSoFar   |  DiscrimType |
|      | result |             | runtime     | (observed)  | (estim.)    |              |
|======================================================================================|
|   21 | Accept |     0.11301 |      4.1129 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.9 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.86 sec
Evaluation completed in 1.1 sec
|   22 | Accept |     0.11354 |      4.2473 |     0.11301 |     0.11301 |    quadratic |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.98 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.87 sec
Evaluation completed in 1.1 sec
|   23 | Accept |     0.11301 |      4.0342 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 1.9 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.88 sec
Evaluation completed in 1.1 sec
|   24 | Accept |     0.11354 |       4.173 |     0.11301 |     0.11301 | pseudoQuadra |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.99 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.82 sec
Evaluation completed in 1.1 sec
|   25 | Accept |     0.11301 |      3.9707 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1 sec
Evaluation completed in 1.7 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.98 sec
Evaluation completed in 1.2 sec
|   26 | Accept |     0.11354 |      4.1135 |     0.11301 |     0.11301 |    quadratic |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 1.1 sec
Evaluation completed in 2 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.92 sec
Evaluation completed in 1.1 sec
|   27 | Accept |     0.11301 |      4.2567 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.94 sec
Evaluation completed in 1.5 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.88 sec
Evaluation completed in 1.1 sec
|   28 | Accept |     0.11301 |      3.7988 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.97 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.88 sec
Evaluation completed in 1.1 sec
|   29 | Accept |     0.11301 |      3.9926 |     0.11301 |     0.11301 | diagQuadrati |
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.95 sec
Evaluation completed in 1.8 sec
Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.85 sec
Evaluation completed in 1 sec
|   30 | Accept |     0.11301 |      3.9793 |     0.11301 |     0.11301 | diagQuadrati |

__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 180.1662 seconds
Total objective function evaluation time: 149.1907

Best observed feasible point:
     DiscrimType 
    _____________

    diagQuadratic

Observed objective function value = 0.11301
Estimated objective function value = 0.11301
Function evaluation time = 4.0594

Best estimated feasible point (according to models):
     DiscrimType 
    _____________

    diagQuadratic

Estimated objective function value = 0.11301
Estimated function evaluation time = 4.1702

Evaluating tall expression using the Parallel Pool 'Processes':
- Pass 1 of 1: Completed in 0.8 sec
Evaluation completed in 1.6 sec

Mdl = 
  CompactClassificationDiscriminant
           PredictorNames: {'x1'  'x2'  'x3'  'x4'  'x5'  'x6'}
             ResponseName: 'Y'
    CategoricalPredictors: []
               ClassNames: [0 1]
           ScoreTransform: 'none'
              DiscrimType: 'diagQuadratic'
                       Mu: [2×6 double]
                   Coeffs: [2×2 struct]


  Properties, Methods

FitInfo = struct with no fields.

HyperparameterOptimizationResults = 
  BayesianOptimization with properties:

                      ObjectiveFcn: @createObjFcn/tallObjFcn
              VariableDescriptions: [1×1 optimizableVariable]
                           Options: [1×1 struct]
                      MinObjective: 0.1130
                   XAtMinObjective: [1×1 table]
             MinEstimatedObjective: 0.1130
          XAtMinEstimatedObjective: [1×1 table]
           NumObjectiveEvaluations: 30
                  TotalElapsedTime: 180.1662
                         NextPoint: [1×1 table]
                            XTrace: [30×1 table]
                    ObjectiveTrace: [30×1 double]
                  ConstraintsTrace: []
                     UserDataTrace: {30×1 cell}
      ObjectiveEvaluationTimeTrace: [30×1 double]
                IterationTimeTrace: [30×1 double]
                        ErrorTrace: [30×1 double]
                  FeasibilityTrace: [30×1 logical]
       FeasibilityProbabilityTrace: [30×1 double]
               IndexOfMinimumTrace: [30×1 double]
             ObjectiveMinimumTrace: [30×1 double]
    EstimatedObjectiveMinimumTrace: [30×1 double]

Input Arguments

collapse all

`Tbl` — Sample data
table

Sample data used to train the model, specified as a table. Each row of Tbl corresponds to one observation, and each column corresponds to one predictor variable. Categorical predictor variables are not supported. Optionally, Tbl can contain one additional column for the response variable, which can be categorical. Multicolumn variables and cell arrays other than cell arrays of character vectors are not allowed.

If Tbl contains the response variable, and you want to use all remaining variables in Tbl as predictors, then specify the response variable by using ResponseVarName.
If Tbl contains the response variable, and you want to use only a subset of the remaining variables in Tbl as predictors, then specify a formula by using formula.
If Tbl does not contain the response variable, then specify a response variable by using Y. The length of the response variable and the number of rows in Tbl must be equal.

`ResponseVarName` — Response variable name
name of variable in `Tbl`

Response variable name, specified as the name of a variable in Tbl.

You must specify ResponseVarName as a character vector or string scalar. For example, if the response variable Y is stored as Tbl.Y, then specify it as "Y". Otherwise, the software treats all columns of Tbl, including Y, as predictors when training the model.

The response variable must be a categorical, character, or string array; a logical or numeric vector; or a cell array of character vectors. If Y is a character array, then each element of the response variable must correspond to one row of the array.

A good practice is to specify the order of the classes by using the ClassNames name-value argument.

Data Types: char | string

`formula` — Explanatory model of response variable and subset of predictor variables
character vector | string scalar

Explanatory model of the response variable and a subset of the predictor variables, specified as a character vector or string scalar in the form "Y~x1+x2+x3". In this form, Y represents the response variable, and x1, x2, and x3 represent the predictor variables.

To specify a subset of variables in Tbl as predictors for training the model, use a formula. If you specify a formula, then the software does not use any variables in Tbl that do not appear in formula.

The variable names in the formula must be both variable names in Tbl (Tbl.Properties.VariableNames) and valid MATLAB^® identifiers. You can verify the variable names in Tbl by using the isvarname function. If the variable names are not valid, then you can convert them by using the matlab.lang.makeValidName function.

Data Types: char | string

`Y` — Class labels
categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

Class labels, specified as a categorical, character, or string array, a logical or numeric vector, or a cell array of character vectors. Each row of Y represents the classification of the corresponding row of X.

The software considers NaN, '' (empty character vector), "" (empty string), <missing>, and <undefined> values in Y to be missing values. Consequently, the software does not train using observations with a missing response.

`X` — Predictor data
numeric matrix

Predictor values, specified as a numeric matrix. Each column of X represents one variable, and each row represents one observation. Categorical predictor variables are not supported.

fitcdiscr considers NaN values in X as missing values. fitcdiscr does not use observations with missing values for X in the fit.

Data Types: single | double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'DiscrimType','quadratic','SaveMemory','on' specifies a quadratic discriminant classifier and does not store the covariance matrix in the output object.

Note

You cannot use any cross-validation name-value argument together with the OptimizeHyperparameters name-value argument. You can modify the cross-validation for OptimizeHyperparameters only by using the HyperparameterOptimizationOptions name-value argument.

Model Parameters

collapse all

`ClassNames` — Names of classes to use for training
categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

Names of classes to use for training, specified as a categorical, character, or string array; a logical or numeric vector; or a cell array of character vectors. ClassNames must have the same data type as the response variable in Tbl or Y.

If ClassNames is a character array, then each element must correspond to one row of the array.

Use ClassNames to:

Specify the order of the classes during training.
Specify the order of any input or output argument dimension that corresponds to the class order. For example, use ClassNames to specify the order of the dimensions of Cost or the column order of classification scores returned by predict.
Select a subset of classes for training. For example, suppose that the set of all distinct class names in Y is ["a","b","c"]. To train the model using observations from classes "a" and "c" only, specify "ClassNames",["a","c"].

The default value for ClassNames is the set of all distinct class names in the response variable in Tbl or Y.

Example: "ClassNames",["b","g"]

`Cost` — Cost of misclassification
square matrix | structure

Cost of misclassification of a point, specified as the comma-separated pair consisting of 'Cost' and one of the following:

Square matrix, where Cost(i,j) is the cost of classifying a point into class j if its true class is i (i.e., the rows correspond to the true class and the columns correspond to the predicted class). To specify the class order for the corresponding rows and columns of Cost, additionally specify the ClassNames name-value pair argument.
Structure S having two fields: S.ClassNames containing the group names as a variable of the same type as Y, and S.ClassificationCosts containing the cost matrix.

The default is Cost(i,j)=1 if i~=j, and Cost(i,j)=0 if i=j.

Data Types: single | double | struct

`Delta` — Linear coefficient threshold
`0` (default) | nonnegative scalar value

Linear coefficient threshold, specified as the comma-separated pair consisting of 'Delta' and a nonnegative scalar value. If a coefficient of Mdl has magnitude smaller than Delta, Mdl sets this coefficient to 0, and you can eliminate the corresponding predictor from the model. Set Delta to a higher value to eliminate more predictors.

Delta must be 0 for quadratic discriminant models.

Data Types: single | double

`DiscrimType` — Discriminant type
`'linear'` (default) | `'quadratic'` | `'diaglinear'` | `'diagquadratic'` | `'pseudolinear'` | `'pseudoquadratic'`

Discriminant type, specified as the comma-separated pair consisting of 'DiscrimType' and a character vector or string scalar in this table.

Value	Description	Predictor Covariance Treatment
`'linear'`	Regularized linear discriminant analysis (LDA)	All classes have the same covariance matrix. ${\hat{Σ}}_{γ} = (1 - γ) \hat{Σ} + γ diag (\hat{Σ}) .$ $\hat{Σ}$ is the empirical, pooled covariance matrix and γ is the amount of regularization.
`'diaglinear'`	LDA	All classes have the same, diagonal covariance matrix.
`'pseudolinear'`	LDA	All classes have the same covariance matrix. The software inverts the covariance matrix using the pseudo inverse.
`'quadratic'`	Quadratic discriminant analysis (QDA)	The covariance matrices can vary among classes.
`'diagquadratic'`	QDA	The covariance matrices are diagonal and can vary among classes.
`'pseudoquadratic'`	QDA	The covariance matrices can vary among classes. The software inverts the covariance matrix using the pseudo inverse.

Note

To use regularization, you must specify 'linear'. To specify the amount of regularization, use the Gamma name-value pair argument.

Example: 'DiscrimType','quadratic'

`FillCoeffs` — `Coeffs` property flag
`'on'` | `'off'`

Coeffs property flag, specified as the comma-separated pair consisting of 'FillCoeffs' and 'on' or 'off'. Setting the flag to 'on' populates the Coeffs property in the classifier object. This can be computationally intensive, especially when cross-validating. The default is 'on', unless you specify a cross-validation name-value pair, in which case the flag is set to 'off' by default.

Example: 'FillCoeffs','off'

`Gamma` — Amount of regularization
scalar value in the interval [0,1]

Amount of regularization to apply when estimating the covariance matrix of the predictors, specified as the comma-separated pair consisting of 'Gamma' and a scalar value in the interval [0,1]. Gamma provides finer control over the covariance matrix structure than DiscrimType.

If you specify 0, then the software does not use regularization to adjust the covariance matrix. That is, the software estimates and uses the unrestricted, empirical covariance matrix.
- For linear discriminant analysis, if the empirical covariance matrix is singular, then the software automatically applies the minimal regularization required to invert the covariance matrix. You can display the chosen regularization amount by entering Mdl.Gamma at the command line.
- For quadratic discriminant analysis, if at least one class has an empirical covariance matrix that is singular, then the software throws an error.
If you specify a value in the interval (0,1), then you must implement linear discriminant analysis, otherwise the software throws an error. Consequently, the software sets DiscrimType to 'linear'.
If you specify 1, then the software uses maximum regularization for covariance matrix estimation. That is, the software restricts the covariance matrix to be diagonal. Alternatively, you can set DiscrimType to 'diagLinear' or 'diagQuadratic' for diagonal covariance matrices.

Example: 'Gamma',1

Data Types: single | double

`PredictorNames` — Predictor variable names
string array of unique names | cell array of unique character vectors

Predictor variable names, specified as a string array of unique names or cell array of unique character vectors. The functionality of PredictorNames depends on the way you supply the training data.

If you supply X and Y, then you can use PredictorNames to assign names to the predictor variables in X.
- The order of the names in PredictorNames must correspond to the column order of X. That is, PredictorNames{1} is the name of X(:,1), PredictorNames{2} is the name of X(:,2), and so on. Also, size(X,2) and numel(PredictorNames) must be equal.
- By default, PredictorNames is {'x1','x2',...}.
If you supply Tbl, then you can use PredictorNames to choose which predictor variables to use in training. That is, fitcdiscr uses only the predictor variables in PredictorNames and the response variable during training.
- PredictorNames must be a subset of Tbl.Properties.VariableNames and cannot include the name of the response variable.
- By default, PredictorNames contains the names of all predictor variables.
- A good practice is to specify the predictors for training using either PredictorNames or formula, but not both.

Example: "PredictorNames",["SepalLength","SepalWidth","PetalLength","PetalWidth"]

Data Types: string | cell

`Prior` — Prior probabilities
`'empirical'` (default) | `'uniform'` | vector of scalar values | structure

Prior probabilities for each class, specified as the comma-separated pair consisting of 'Prior' and a value in this table.

Value	Description
`'empirical'`	The class prior probabilities are the class relative frequencies in `Y`.
`'uniform'`	All class prior probabilities are equal to 1/K, where K is the number of classes.
numeric vector	Each element is a class prior probability. Order the elements according to `Mdl.ClassNames` or specify the order using the `ClassNames` name-value pair argument. The software normalizes the elements such that they sum to `1`.
structure	A structure `S` with two fields: `S.ClassNames` contains the class names as a variable of the same type as `Y`. `S.ClassProbs` contains a vector of corresponding prior probabilities. The software normalizes the elements such that they sum to `1`.

If you set values for both Weights and Prior, the weights are renormalized to add up to the value of the prior probability in the respective class.

Example: 'Prior','uniform'

Data Types: char | string | single | double | struct

`ResponseName` — Response variable name
`"Y"` (default) | character vector | string scalar

Response variable name, specified as a character vector or string scalar.

If you supply Y, then you can use ResponseName to specify a name for the response variable.
If you supply ResponseVarName or formula, then you cannot use ResponseName.

Example: ResponseName="response"

Data Types: char | string

`SaveMemory` — Flag to save covariance matrix
`'off'` (default) | `'on'`

Flag to save covariance matrix, specified as the comma-separated pair consisting of 'SaveMemory' and either 'on' or 'off'. If you specify 'on', then fitcdiscr does not store the full covariance matrix, but instead stores enough information to compute the matrix. The predict method computes the full covariance matrix for prediction, and does not store the matrix. If you specify 'off', then fitcdiscr computes and stores the full covariance matrix in Mdl.

Specify SaveMemory as 'on' when the input matrix contains thousands of predictors.

Example: 'SaveMemory','on'

`ScoreTransform` — Score transformation
`"none"` (default) | `"doublelogit"` | `"invlogit"` | `"ismax"` | `"logit"` | function handle | ...

Score transformation, specified as a character vector, string scalar, or function handle.

This table summarizes the available character vectors and string scalars.

Value	Description
`"doublelogit"`	1/(1 + e^–2x)
`"invlogit"`	log(x / (1 – x))
`"ismax"`	Sets the score for the class with the largest score to 1, and sets the scores for all other classes to 0
`"logit"`	1/(1 + e^–x)
`"none"` or `"identity"`	x (no transformation)
`"sign"`	–1 for x < 0 0 for x = 0 1 for x > 0
`"symmetric"`	2x – 1
`"symmetricismax"`	Sets the score for the class with the largest score to 1, and sets the scores for all other classes to –1
`"symmetriclogit"`	2/(1 + e^–x) – 1

For a MATLAB function or a function you define, use its function handle for the score transform. The function handle must accept a matrix (the original scores) and return a matrix of the same size (the transformed scores).

Example: "ScoreTransform","logit"

Data Types: char | string | function_handle

`Weights` — Observation weights
numeric vector of positive values | name of variable in `Tbl`

Observation weights, specified as the comma-separated pair consisting of 'Weights' and a numeric vector of positive values or name of a variable in Tbl. The software weighs the observations in each row of X or Tbl with the corresponding value in Weights. The size of Weights must equal the number of rows of X or Tbl.

If you specify the input data as a table Tbl, then Weights can be the name of a variable in Tbl that contains a numeric vector. In this case, you must specify Weights as a character vector or string scalar. For example, if the weights vector W is stored as Tbl.W, then specify it as 'W'. Otherwise, the software treats all columns of Tbl, including W, as predictors or the response when training the model.

The software normalizes Weights to sum up to the value of the prior probability in the respective class.

By default, Weights is ones(n,1), where n is the number of observations in X or Tbl.

Data Types: double | single | char | string

Cross-Validation Options

collapse all

`CrossVal` — Cross-validation flag
`'off'` (default) | `'on'`

Cross-validation flag, specified as the comma-separated pair consisting of 'Crossval' and 'on' or 'off'.

If you specify 'on', then the software implements 10-fold cross-validation.

To override this cross-validation setting, use one of these name-value pair arguments: CVPartition, Holdout, KFold, or Leaveout. To create a cross-validated model, you can use one cross-validation name-value pair argument at a time only.

Alternatively, cross-validate later by passing Mdl to crossval.

Example: 'CrossVal','on'

`CVPartition` — Cross-validation partition
`[]` (default) | `cvpartition` object

Cross-validation partition, specified as a cvpartition object that specifies the type of cross-validation and the indexing for the training and validation sets.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: Suppose you create a random partition for 5-fold cross-validation on 500 observations by using cvp = cvpartition(500,KFold=5). Then, you can specify the cross-validation partition by setting CVPartition=cvp.

`Holdout` — Fraction of data for holdout validation
scalar value in the range (0,1)

Fraction of the data used for holdout validation, specified as a scalar value in the range (0,1). If you specify Holdout=p, then the software completes these steps:

Randomly select and reserve p*100% of the data as validation data, and train the model using the rest of the data.
Store the compact trained model in the Trained property of the cross-validated model.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: Holdout=0.1

Data Types: double | single

`KFold` — Number of folds
`10` (default) | positive integer value greater than 1

Number of folds to use in the cross-validated model, specified as a positive integer value greater than 1. If you specify KFold=k, then the software completes these steps:

Randomly partition the data into k sets.
For each set, reserve the set as validation data, and train the model using the other k – 1 sets.
Store the k compact trained models in a k-by-1 cell vector in the Trained property of the cross-validated model.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: KFold=5

Data Types: single | double

`Leaveout` — Leave-one-out cross-validation flag
`"off"` (default) | `"on"`

Leave-one-out cross-validation flag, specified as "on" or "off". If you specify Leaveout="on", then for each of the n observations (where n is the number of observations, excluding missing observations, specified in the NumObservations property of the model), the software completes these steps:

Reserve the one observation as validation data, and train the model using the other n – 1 observations.
Store the n compact trained models in an n-by-1 cell vector in the Trained property of the cross-validated model.

To create a cross-validated model, you can specify only one of these four name-value arguments: CVPartition, Holdout, KFold, or Leaveout.

Example: Leaveout="on"

Data Types: char | string

Hyperparameter Optimization Options

collapse all

`OptimizeHyperparameters` — Parameters to optimize
`'none'` (default) | `'auto'` | `'all'` | string array or cell array of eligible parameter names | vector of `optimizableVariable` objects

Parameters to optimize, specified as the comma-separated pair consisting of 'OptimizeHyperparameters' and one of the following:

'none' — Do not optimize.
'auto' — Use {'Delta','Gamma'}.
'all' — Optimize all eligible parameters.
String array or cell array of eligible parameter names.
Vector of optimizableVariable objects, typically the output of hyperparameters.

The optimization attempts to minimize the cross-validation loss (error) for fitcdiscr by varying the parameters. To control the cross-validation type and other aspects of the optimization, use the HyperparameterOptimizationOptions name-value argument. When you use HyperparameterOptimizationOptions, you can use the (compact) model size instead of the cross-validation loss as the optimization objective by setting the ConstraintType and ConstraintBounds options.

Note

The values of OptimizeHyperparameters override any values you specify using other name-value arguments. For example, setting OptimizeHyperparameters to "auto" causes fitcdiscr to optimize hyperparameters corresponding to the "auto" option and to ignore any specified values for the hyperparameters.

The eligible parameters for fitcdiscr are:

Delta — fitcdiscr searches among positive values, by default log-scaled in the range [1e-6,1e3].
DiscrimType — fitcdiscr searches among 'linear', 'quadratic', 'diagLinear', 'diagQuadratic', 'pseudoLinear', and 'pseudoQuadratic'.
Gamma — fitcdiscr searches among real values in the range [0,1].

Set nondefault parameters by passing a vector of optimizableVariable objects that have nondefault values. For example,

load fisheriris
params = hyperparameters('fitcdiscr',meas,species);
params(1).Range = [1e-4,1e6];

Pass params as the value of OptimizeHyperparameters.

By default, the iterative display appears at the command line, and plots appear according to the number of hyperparameters in the optimization. For the optimization and plots, the objective function is the misclassification rate. To control the iterative display, set the Verbose option of the HyperparameterOptimizationOptions name-value argument. To control the plots, set the ShowPlots field of the HyperparameterOptimizationOptions name-value argument.

For an example, see Optimize Discriminant Analysis Model.

Example: 'auto'

`HyperparameterOptimizationOptions` — Options for optimization
`HyperparameterOptimizationOptions` object | structure

Options for optimization, specified as a HyperparameterOptimizationOptions object or a structure. This argument modifies the effect of the OptimizeHyperparameters name-value argument. If you specify HyperparameterOptimizationOptions, you must also specify OptimizeHyperparameters. All the options are optional. However, you must set ConstraintBounds and ConstraintType to return AggregateOptimizationResults. The options that you can set in a structure are the same as those in the HyperparameterOptimizationOptions object.

Option	Values	Default
`Optimizer`	`"bayesopt"` — Use Bayesian optimization. Internally, this setting calls `bayesopt`. `"gridsearch"` — Use grid search with `NumGridDivisions` values per dimension. `"gridsearch"` searches in a random order, using uniform sampling without replacement from the grid. After optimization, you can get a table in grid order by using the command `sortrows(Mdl.HyperparameterOptimizationResults)`. `"randomsearch"` — Search at random among `MaxObjectiveEvaluations` points.	`"bayesopt"`
`ConstraintBounds`	Constraint bounds for N optimization problems, specified as an N-by-2 numeric matrix or `[]`. The columns of `ConstraintBounds` contain the lower and upper bound values of the optimization problems. If you specify `ConstraintBounds` as a numeric vector, the software assigns the values to the second column of `ConstraintBounds`, and zeros to the first column. If you specify `ConstraintBounds`, you must also specify `ConstraintType`.	`[]`
`ConstraintTarget`	Constraint target for the optimization problems, specified as `"matlab"` or `"coder"`. If `ConstraintBounds` and `ConstraintType` are `[]` and you set `ConstraintTarget`, then the software sets `ConstraintTarget` to `[]`. The values of `ConstraintTarget` and `ConstraintType` determine the objective and constraint functions. For more information, see `HyperparameterOptimizationOptions`.	If you specify `ConstraintBounds` and `ConstraintType`, then the default value is `"matlab"`. Otherwise, the default value is `[]`.
`ConstraintType`	Constraint type for the optimization problems, specified as `"size"` or `"loss"`. If you specify `ConstraintType`, you must also specify `ConstraintBounds`. The values of `ConstraintTarget` and `ConstraintType` determine the objective and constraint functions. For more information, see `HyperparameterOptimizationOptions`.	`[]`
`AcquisitionFunctionName`	Type of acquisition function: `"expected-improvement-per-second-plus"` `"expected-improvement"` `"expected-improvement-plus"` `"expected-improvement-per-second"` `"lower-confidence-bound"` `"probability-of-improvement"` Acquisition functions whose names include `per-second` do not yield reproducible results, because the optimization depends on the run time of the objective function. Acquisition functions whose names include `plus` modify their behavior when they overexploit an area. For more details, see Acquisition Function Types.	`"expected-improvement-per-second-plus"`
`MaxObjectiveEvaluations`	Maximum number of objective function evaluations. If you specify multiple optimization problems using `ConstraintBounds`, the value of `MaxObjectiveEvaluations` applies to each optimization problem individually.	`30` for `"bayesopt"` and `"randomsearch"`, and the entire grid for `"gridsearch"`
`MaxTime`	Time limit for the optimization, specified as a nonnegative real scalar. The time limit is in seconds, as measured by `tic` and `toc`. The software performs at least one optimization iteration, regardless of the value of `MaxTime`. The run time can exceed `MaxTime` because `MaxTime` does not interrupt function evaluations. If you specify multiple optimization problems using `ConstraintBounds`, the time limit applies to each optimization problem individually.	`Inf`
`NumGridDivisions`	For `Optimizer="gridsearch"`, the number of values in each dimension. The value can be a vector of positive integers giving the number of values for each dimension, or a scalar that applies to all dimensions. This option is ignored for categorical variables.	`10`
`ShowPlots`	Logical value indicating whether to show plots of the optimization progress. If this option is `true`, the software plots the best observed objective function value against the iteration number. If you use Bayesian optimization (`Optimizer="bayesopt"`), then the software also plots the best estimated objective function value. The best observed objective function values and best estimated objective function values correspond to the values in the `BestSoFar (observed)` and `BestSoFar (estim.)` columns of the iterative display, respectively. You can find these values in the properties `ObjectiveMinimumTrace` and `EstimatedObjectiveMinimumTrace` of `Mdl.HyperparameterOptimizationResults`. If the problem includes one or two optimization parameters for Bayesian optimization, then `ShowPlots` also plots a model of the objective function against the parameters.	`true`
`SaveIntermediateResults`	Logical value indicating whether to save the optimization results. If this option is `true`, the software overwrites a workspace variable named `"BayesoptResults"` at each iteration. The variable is a `BayesianOptimization` object. If you specify multiple optimization problems using `ConstraintBounds`, the workspace variable is an `AggregateBayesianOptimization` object named `"AggregateBayesoptResults"`.	`false`
`Verbose`	Display level at the command line: `0` — No iterative display `1` — Iterative display `2` — Iterative display with additional information For details, see the `bayesopt` `Verbose` name-value argument and the example Optimize Classifier Fit Using Bayesian Optimization.	`1`
`UseParallel`	Logical value indicating whether to run the Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization.	`false`
`Repartition`	Logical value indicating whether to repartition the cross-validation at every iteration. If this option is `false`, the optimizer uses a single partition for the optimization. A value of `true` usually gives the most robust results because this setting takes partitioning noise into account. However, for optimal results, `true` requires at least twice as many function evaluations.	`false`
Specify only one of the following three options.
`CVPartition`	`cvpartition` object created by `cvpartition`	`Kfold=5` if you do not specify a cross-validation option
`Holdout`	Scalar in the range `(0,1)` representing the holdout fraction
`Kfold`	Integer greater than 1

Example: HyperparameterOptimizationOptions=struct(UseParallel=true)

Output Arguments

collapse all

`Mdl` — Trained discriminant analysis classification model
`ClassificationDiscriminant` model object | `ClassificationPartitionedModel` cross-validated model object

Trained discriminant analysis classification model, returned as a ClassificationDiscriminant model object or a ClassificationPartitionedModel cross-validated model object.

If you set any of the name-value pair arguments KFold, Holdout, CrossVal, or CVPartition, then Mdl is a ClassificationPartitionedModel cross-validated model object. Otherwise, Mdl is a ClassificationDiscriminant model object.

To reference properties of Mdl, use dot notation. For example, to display the estimated component means at the Command Window, enter Mdl.Mu.

If you specify OptimizeHyperparameters and set the ConstraintType and ConstraintBounds options of HyperparameterOptimizationOptions, then Mdl is an N-by-1 cell array of model objects, where N is equal to the number of rows in ConstraintBounds. If none of the optimization problems yields a feasible model, then each cell array value is [].

`AggregateOptimizationResults` — Aggregate optimization results
`AggregateBayesianOptimization` object

Aggregate optimization results for multiple optimization problems, returned as an AggregateBayesianOptimization object. To return AggregateOptimizationResults, you must specify OptimizeHyperparameters and HyperparameterOptimizationOptions. You must also specify the ConstraintType and ConstraintBounds options of HyperparameterOptimizationOptions. For an example that shows how to produce this output, see Hyperparameter Optimization with Multiple Constraint Bounds.

More About

collapse all

Discriminant Classification

The model for discriminant analysis is:

Each class (Y) generates data (X) using a multivariate normal distribution. That is, the model assumes X has a Gaussian mixture distribution (gmdistribution).
- For linear discriminant analysis, the model has the same covariance matrix for each class, only the means vary.
- For quadratic discriminant analysis, both means and covariances of each class vary.

predict classifies so as to minimize the expected classification cost:

$\hat{y} = \underset{y = 1, ..., K}{\arg \min} \sum_{k = 1}^{K} \hat{P} (k | x) C (y | k),$

where

$\hat{y}$ is the predicted classification.
K is the number of classes.
$\hat{P} (k | x)$ is the posterior probability of class k for observation x.
$C (y | k)$ is the cost of classifying an observation as y when its true class is k.

For details, see Prediction Using Discriminant Analysis Models.

Tips

After training a model, you can generate C/C++ code that predicts labels for new data. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.

Algorithms

If you specify the Cost, Prior, and Weights name-value arguments, the output model object stores the specified values in the Cost, Prior, and W properties, respectively. The Cost property stores the user-specified cost matrix as is. The Prior and W properties store the prior probabilities and observation weights, respectively, after normalization. For details, see Misclassification Cost Matrix, Prior Probabilities, and Observation Weights.
The software uses the Cost property for prediction, but not training. Therefore, Cost is not read-only; you can change the property value by using dot notation after creating the trained model.

Alternative Functionality

Functions

The classify function also performs discriminant analysis. classify is usually more awkward to use.

classify requires you to fit the classifier every time you make a new prediction.
classify does not perform cross-validation or hyperparameter optimization.
classify requires you to fit the classifier when changing prior probabilities.

Extended Capabilities

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

The fitcdiscr function supports tall arrays with the following usage notes and limitations:

For more information, see Tall Arrays.

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

To perform parallel hyperparameter optimization, use the UseParallel=true option in the HyperparameterOptimizationOptions name-value argument in the call to the fitcdiscr function.

For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.

For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).

Version History

Introduced in R2014a

fitcdiscr

Syntax

Description

Examples

Train Discriminant Analysis Model

Optimize Discriminant Analysis Model

Optimize Discriminant Analysis Model on Tall Array

Input Arguments

Tbl — Sample data table

ResponseVarName — Response variable name name of variable in Tbl

formula — Explanatory model of response variable and subset of predictor variables character vector | string scalar

Y — Class labels categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

X — Predictor data numeric matrix

Name-Value Arguments

ClassNames — Names of classes to use for training categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

Cost — Cost of misclassification square matrix | structure

Delta — Linear coefficient threshold 0 (default) | nonnegative scalar value

DiscrimType — Discriminant type 'linear' (default) | 'quadratic' | 'diaglinear' | 'diagquadratic' | 'pseudolinear' | 'pseudoquadratic'

FillCoeffs — Coeffs property flag 'on' | 'off'

Gamma — Amount of regularization scalar value in the interval [0,1]

PredictorNames — Predictor variable names string array of unique names | cell array of unique character vectors

Prior — Prior probabilities 'empirical' (default) | 'uniform' | vector of scalar values | structure

ResponseName — Response variable name "Y" (default) | character vector | string scalar

SaveMemory — Flag to save covariance matrix 'off' (default) | 'on'

ScoreTransform — Score transformation "none" (default) | "doublelogit" | "invlogit" | "ismax" | "logit" | function handle | ...

Weights — Observation weights numeric vector of positive values | name of variable in Tbl

CrossVal — Cross-validation flag 'off' (default) | 'on'

CVPartition — Cross-validation partition [] (default) | cvpartition object

Holdout — Fraction of data for holdout validation scalar value in the range (0,1)

KFold — Number of folds 10 (default) | positive integer value greater than 1

Leaveout — Leave-one-out cross-validation flag "off" (default) | "on"

OptimizeHyperparameters — Parameters to optimize 'none' (default) | 'auto' | 'all' | string array or cell array of eligible parameter names | vector of optimizableVariable objects

HyperparameterOptimizationOptions — Options for optimization HyperparameterOptimizationOptions object | structure

Output Arguments

Mdl — Trained discriminant analysis classification model ClassificationDiscriminant model object | ClassificationPartitionedModel cross-validated model object

AggregateOptimizationResults — Aggregate optimization results AggregateBayesianOptimization object

More About

Discriminant Classification

Tips

Algorithms

Alternative Functionality

Functions

Extended Capabilities

Tall Arrays Calculate with arrays that have more rows than fit in memory.

Automatic Parallel Support Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

Version History

See Also

Topics

`Tbl` — Sample data
table

`ResponseVarName` — Response variable name
name of variable in `Tbl`

`formula` — Explanatory model of response variable and subset of predictor variables
character vector | string scalar

`Y` — Class labels
categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

`X` — Predictor data
numeric matrix

`ClassNames` — Names of classes to use for training
categorical array | character array | string array | logical vector | numeric vector | cell array of character vectors

`Cost` — Cost of misclassification
square matrix | structure

`Delta` — Linear coefficient threshold
`0` (default) | nonnegative scalar value

`DiscrimType` — Discriminant type
`'linear'` (default) | `'quadratic'` | `'diaglinear'` | `'diagquadratic'` | `'pseudolinear'` | `'pseudoquadratic'`

`FillCoeffs` — `Coeffs` property flag
`'on'` | `'off'`

`Gamma` — Amount of regularization
scalar value in the interval [0,1]

`PredictorNames` — Predictor variable names
string array of unique names | cell array of unique character vectors

`Prior` — Prior probabilities
`'empirical'` (default) | `'uniform'` | vector of scalar values | structure

`ResponseName` — Response variable name
`"Y"` (default) | character vector | string scalar

`SaveMemory` — Flag to save covariance matrix
`'off'` (default) | `'on'`

`ScoreTransform` — Score transformation
`"none"` (default) | `"doublelogit"` | `"invlogit"` | `"ismax"` | `"logit"` | function handle | ...

`Weights` — Observation weights
numeric vector of positive values | name of variable in `Tbl`

`CrossVal` — Cross-validation flag
`'off'` (default) | `'on'`

`CVPartition` — Cross-validation partition
`[]` (default) | `cvpartition` object

`Holdout` — Fraction of data for holdout validation
scalar value in the range (0,1)

`KFold` — Number of folds
`10` (default) | positive integer value greater than 1

`Leaveout` — Leave-one-out cross-validation flag
`"off"` (default) | `"on"`

`OptimizeHyperparameters` — Parameters to optimize
`'none'` (default) | `'auto'` | `'all'` | string array or cell array of eligible parameter names | vector of `optimizableVariable` objects

`HyperparameterOptimizationOptions` — Options for optimization
`HyperparameterOptimizationOptions` object | structure

`Mdl` — Trained discriminant analysis classification model
`ClassificationDiscriminant` model object | `ClassificationPartitionedModel` cross-validated model object

`AggregateOptimizationResults` — Aggregate optimization results
`AggregateBayesianOptimization` object

Tall Arrays
Calculate with arrays that have more rows than fit in memory.

Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.