Main Content

perfcurve

Receiver operating characteristic (ROC) curve or other performance curve for classifier output

collapse all in page

Syntax

[X,Y] = perfcurve(labels,scores,posclass)
[X,Y,T] = perfcurve(labels,scores,posclass)
[X,Y,T,AUC] = perfcurve(labels,scores,posclass)
[X,Y,T,AUC,OPTROCPT] = perfcurve(labels,scores,posclass)
[X,Y,T,AUC,OPTROCPT,SUBY] = perfcurve(labels,scores,posclass)
[X,Y,T,AUC,OPTROCPT,SUBY,SUBYNAMES] = perfcurve(labels,scores,posclass)
[___] = perfcurve(labels,scores,posclass,Name,Value)

Description

[X,Y] = perfcurve(labels,scores,posclass) returns the X and Y coordinates of an ROC curve for a vector of classifier predictions, scores, given true class labels, labels, and the positive class label, posclass. You can visualize the performance curve using plot(X,Y).

example

[X,Y,T] = perfcurve(labels,scores,posclass) returns an array of thresholds on classifier scores for the computed values of X and Y.

[X,Y,T,AUC] = perfcurve(labels,scores,posclass) returns the area under the curve for the computed values of X and Y.

example

[X,Y,T,AUC,OPTROCPT] = perfcurve(labels,scores,posclass) returns the optimal operating point of the ROC curve.

example

[X,Y,T,AUC,OPTROCPT,SUBY] = perfcurve(labels,scores,posclass) returns the Y values for negative subclasses.

[X,Y,T,AUC,OPTROCPT,SUBY,SUBYNAMES] = perfcurve(labels,scores,posclass) returns the negative class names.

example

[___] = perfcurve(labels,scores,posclass,Name,Value) returns the coordinates of a ROC curve and any other output argument from the previous syntaxes, with additional options specified by one or more Name,Value pair arguments.

For example, you can provide a list of negative classes, change the X or Y criterion, compute pointwise confidence bounds using cross validation or bootstrap, specify the misclassification cost, or compute the confidence bounds in parallel.

Examples

collapse all

Open Live Script

Load the sample data.

load fisheriris

Use only the first two features as predictor variables. Define a binary classification problem by using only the measurements that correspond to the species versicolor and virginica.

pred = meas(51:end,1:2);

Define the binary response variable.

resp = (1:100)'>50;  % Versicolor = 0, virginica = 1

Fit a logistic regression model.

mdl = fitglm(pred,resp,'Distribution','binomial','Link','logit');

Compute the ROC curve. Use the probability estimates from the logistic regression model as scores.

scores = mdl.Fitted.Probability;
[X,Y,T,AUC] = perfcurve(species(51:end,:),scores,'virginica');

perfcurve stores the threshold values in the array T.

Display the area under the curve.

AUC
AUC = 
0.7918

The area under the curve is 0.7918. The maximum AUC is 1, which corresponds to a perfect classifier. Larger AUC values indicate better classifier performance.

Plot the ROC curve.

plot(X,Y)
xlabel('False positive rate') 
ylabel('True positive rate')
title('ROC for Classification by Logistic Regression')

Figure contains an axes object. The axes object with title ROC for Classification by Logistic Regression, xlabel False positive rate, ylabel True positive rate contains an object of type line.

Alternatively, you can compute and plot the ROC curve by creating a rocmetrics object and using the object function plot. 

rocObj = rocmetrics(species(51:end,:),scores,'virginica');
plot(rocObj)

Figure contains an axes object. The axes object with title ROC Curve, xlabel False Positive Rate, ylabel True Positive Rate contains 3 objects of type roccurve, scatter, line. These objects represent virginica (AUC = 0.7918), virginica Model Operating Point.

The plot function displays a filled circle at the model operating point, and the legend displays the class name and AUC value for the curve.

Open Live Script

Load the sample data.

load ionosphere

X is a 351x34 real-valued matrix of predictors. Y is a character array of class labels: 'b' for bad radar returns and 'g' for good radar returns.

Reformat the response to fit a logistic regression. Use the predictor variables 3 through 34.

resp = strcmp(Y,'b'); % resp = 1, if Y = 'b', or 0 if Y = 'g' 
pred = X(:,3:34);

Fit a logistic regression model to estimate the posterior probabilities for a radar return to be a bad one.

mdl = fitglm(pred,resp,'Distribution','binomial','Link','logit');
score_log = mdl.Fitted.Probability; % Probability estimates

Compute the standard ROC curve using the probabilities for scores.

[Xlog,Ylog,Tlog,AUClog] = perfcurve(resp,score_log,'true');

Train an SVM classifier on the same sample data. Standardize the data.

mdlSVM = fitcsvm(pred,resp,'Standardize',true);

Compute the posterior probabilities (scores).

mdlSVM = fitPosterior(mdlSVM);
[~,score_svm] = resubPredict(mdlSVM);

The second column of score_svm contains the posterior probabilities of bad radar returns.

Compute the standard ROC curve using the scores from the SVM model.

[Xsvm,Ysvm,Tsvm,AUCsvm] = perfcurve(resp,score_svm(:,mdlSVM.ClassNames),'true');

Fit a naive Bayes classifier on the same sample data.

mdlNB = fitcnb(pred,resp);

Compute the posterior probabilities (scores).

[~,score_nb] = resubPredict(mdlNB);

Compute the standard ROC curve using the scores from the naive Bayes classification.

[Xnb,Ynb,Tnb,AUCnb] = perfcurve(resp,score_nb(:,mdlNB.ClassNames),'true');

Plot the ROC curves on the same graph.

plot(Xlog,Ylog)
hold on
plot(Xsvm,Ysvm)
plot(Xnb,Ynb)
legend('Logistic Regression','Support Vector Machines','Naive Bayes','Location','Best')
xlabel('False positive rate'); ylabel('True positive rate');
title('ROC Curves for Logistic Regression, SVM, and Naive Bayes Classification')
hold off

Figure contains an axes object. The axes object with title ROC Curves for Logistic Regression, SVM, and Naive Bayes Classification, xlabel False positive rate, ylabel True positive rate contains 3 objects of type line. These objects represent Logistic Regression, Support Vector Machines, Naive Bayes.

Although SVM produces better ROC values for higher thresholds, logistic regression is usually better at distinguishing the bad radar returns from the good ones. The ROC curve for naive Bayes is generally lower than the other two ROC curves, which indicates worse in-sample performance than the other two classifier methods.

Compare the area under the curve for all three classifiers.

AUClog
AUClog = 
0.9659

AUCsvm
AUCsvm = 
0.9489

AUCnb
AUCnb = 
0.9393

Logistic regression has the highest AUC measure for classification and naive Bayes has the lowest. This result suggests that logistic regression has better in-sample average performance for this sample data.

Open Script

This example shows how to determine the better parameter value for a custom kernel function in a classifier using the ROC curves.

Generate a random set of points within the unit circle.

rng(1);  % For reproducibility
n = 100; % Number of points per quadrant

r1 = sqrt(rand(2*n,1));                     % Random radii
t1 = [pi/2*rand(n,1); (pi/2*rand(n,1)+pi)]; % Random angles for Q1 and Q3
X1 = [r1.*cos(t1) r1.*sin(t1)];             % Polar-to-Cartesian conversion

r2 = sqrt(rand(2*n,1));
t2 = [pi/2*rand(n,1)+pi/2; (pi/2*rand(n,1)-pi/2)]; % Random angles for Q2 and Q4
X2 = [r2.*cos(t2) r2.*sin(t2)];

Define the predictor variables. Label points in the first and third quadrants as belonging to the positive class, and those in the second and fourth quadrants in the negative class.

pred = [X1; X2];
resp = ones(4*n,1);
resp(2*n + 1:end) = -1; % Labels

Create the function mysigmoid.m , which accepts two matrices in the feature space as inputs, and transforms them into a Gram matrix using the sigmoid kernel.

function G = mysigmoid(U,V)
% Sigmoid kernel function with slope gamma and intercept c
gamma = 1;
c = -1;
G = tanh(gamma*U*V' + c);
end

Train an SVM classifier using the sigmoid kernel function. It is good practice to standardize the data.

SVMModel1 = fitcsvm(pred,resp,'KernelFunction','mysigmoid',...
				'Standardize',true);
SVMModel1 = fitPosterior(SVMModel1);
[~,scores1] = resubPredict(SVMModel1);

Set gamma = 0.5 ; within mysigmoid.m and save as mysigmoid2.m. And, train an SVM classifier using the adjusted sigmoid kernel.

function G = mysigmoid2(U,V)
% Sigmoid kernel function with slope gamma and intercept c
gamma = 0.5;
c = -1;
G = tanh(gamma*U*V' + c);
end


SVMModel2 = fitcsvm(pred,resp,'KernelFunction','mysigmoid2',...
				'Standardize',true);
SVMModel2 = fitPosterior(SVMModel2);
[~,scores2] = resubPredict(SVMModel2);

Compute the ROC curves and the area under the curve (AUC) for both models.

[x1,y1,~,auc1] = perfcurve(resp,scores1(:,2),1);
[x2,y2,~,auc2] = perfcurve(resp,scores2(:,2),1);

Plot the ROC curves.

plot(x1,y1)
hold on
plot(x2,y2)
hold off
legend('gamma = 1','gamma = 0.5','Location','SE');
xlabel('False positive rate'); ylabel('True positive rate');
title('ROC for classification by SVM');

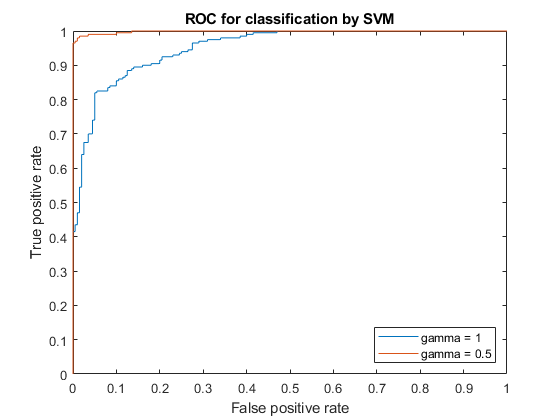
The kernel function with the gamma parameter set to 0.5 gives better in-sample results.

Compare the AUC measures.

auc1
auc2

auc1 =

    0.9518


auc2 =

    0.9985

The area under the curve for gamma set to 0.5 is higher than that for gamma set to 1. This also confirms that gamma parameter value of 0.5 produces better results. For visual comparison of the classification performance with these two gamma parameter values, see Train SVM Classifier Using Custom Kernel.

Open Live Script

Load the sample data.

load fisheriris

The column vector, species, consists of iris flowers of three different species: setosa, versicolor, virginica. The double matrix meas consists of four types of measurements on the flowers: sepal length, sepal width, petal length, and petal width. All measures are in centimeters.

Train a classification tree using the sepal length and width as the predictor variables. It is a good practice to specify the class names.

Model = fitctree(meas(:,1:2),species, ...
    'ClassNames',{'setosa','versicolor','virginica'});

Predict the class labels and scores for the species based on the tree Model.

[~,score] = resubPredict(Model);

The scores are the posterior probabilities that an observation (a row in the data matrix) belongs to a class. The columns of score correspond to the classes specified by 'ClassNames'. So, the first column corresponds to setosa, the second corresponds to versicolor, and the third column corresponds to virginica.

Compute the ROC curve for the predictions that an observation belongs to versicolor, given the true class labels species. Also compute the optimal operating point and y values for negative subclasses. Return the names of the negative classes.

Because this is a multiclass problem, you cannot merely supply score(:,2) as input to perfcurve. Doing so would not give perfcurve enough information about the scores for the two negative classes (setosa and virginica). This problem is unlike a binary classification problem, where knowing the scores of one class is enough to determine the scores of the other class. Therefore, you must supply perfcurve with a function that factors in the scores of the two negative classes. One such function is score(:,2)-max(score(:,1),score(:,3)), which corresponds to the one-versus-all coding design. 

diffscore1 = score(:,2) - max(score(:,1),score(:,3));

The values in diffscore are classification scores for a binary problem that treats the second class as a positive class and the rest as negative classes. 

[X,Y,T,~,OPTROCPT,suby,subnames] = perfcurve(species,diffscore1,'versicolor');

X, by default, is the false positive rate (fallout or 1-specificity) and Y, by default, is the true positive rate (recall or sensitivity). The positive class label is versicolor. Because a negative class is not defined, perfcurve assumes that the observations that do not belong to the positive class are in one class. The function accepts it as the negative class.

OPTROCPT
OPTROCPT = 1×2

    0.1000    0.8000


suby
suby = 12×2

         0         0
    0.1800    0.1800
    0.4800    0.4800
    0.5800    0.5800
    0.6200    0.6200
    0.8000    0.8000
    0.8800    0.8800
    0.9200    0.9200
    0.9600    0.9600
    0.9800    0.9800
      ⋮


subnames
subnames = 1x2 cell
    {'setosa'}    {'virginica'}

Plot the ROC curve and the optimal operating point on the ROC curve.

plot(X,Y)
hold on
plot(OPTROCPT(1),OPTROCPT(2),'ro')
xlabel('False positive rate') 
ylabel('True positive rate')
title('ROC Curve for Classification by Classification Trees')
hold off

Figure contains an axes object. The axes object with title ROC Curve for Classification by Classification Trees, xlabel False positive rate, ylabel True positive rate contains 2 objects of type line. One or more of the lines displays its values using only markers

Find the threshold that corresponds to the optimal operating point.

T((X==OPTROCPT(1))&(Y==OPTROCPT(2)))
ans = 
0.2857

Specify virginica as the negative class and compute and plot the ROC curve for versicolor.

Again, you must supply perfcurve with a function that factors in the scores of the negative class. An example of a function to use is score(:,2)-score(:,3). 

diffscore2 = score(:,2) - score(:,3);
[X,Y,~,~,OPTROCPT] = perfcurve(species,diffscore2,'versicolor', ...
    'negClass','virginica');
OPTROCPT
OPTROCPT = 1×2

    0.1800    0.8200


figure, plot(X,Y)
hold on
plot(OPTROCPT(1),OPTROCPT(2),'ro')
xlabel('False positive rate') 
ylabel('True positive rate')
title('ROC Curve for Classification by Classification Trees')
hold off

Figure contains an axes object. The axes object with title ROC Curve for Classification by Classification Trees, xlabel False positive rate, ylabel True positive rate contains 2 objects of type line. One or more of the lines displays its values using only markers

Alternatively, you can use a rocmetrics object to create the ROC curve. rocmetrics supports multiclass classification problems using the one-versus-all coding design, which reduces a multiclass problem into a set of binary problems. You can examine the performance of a multiclass problem on each class by plotting a one-versus-all ROC curve for each class.

Compute the performance metrics by creating a rocmetrics object. Specify the true labels, classification scores, and class names.

rocObj = rocmetrics(species,score,Model.ClassNames);

Plot the ROC curve for each class by using the plot function of rocmetrics. 

figure
plot(rocObj)

Figure contains an axes object. The axes object with title ROC Curve, xlabel False Positive Rate, ylabel True Positive Rate contains 7 objects of type roccurve, scatter, line. These objects represent setosa (AUC = 0.993), setosa Model Operating Point, versicolor (AUC = 0.9358), versicolor Model Operating Point, virginica (AUC = 0.951), virginica Model Operating Point.

The plot function displays a filled circle at the model operating point for each class, and the legend shows the class name and AUC value for each curve. You can find the optimal operating points by using the properties stored in the rocmetrics object rocObj. For an example, see Find Model Operating Point and Optimal Operating Point.

Open Live Script

Load the sample data.

load fisheriris

The column vector species consists of iris flowers of three different species: setosa, versicolor, virginica. The double matrix meas consists of four types of measurements on the flowers: sepal length, sepal width, petal length, and petal width. All measures are in centimeters.

Use only the first two features as predictor variables. Define a binary problem by using only the measurements that correspond to the versicolor and virginica species.

pred = meas(51:end,1:2);

Define the binary response variable.

resp = (1:100)'>50;  % Versicolor = 0, virginica = 1

Fit a logistic regression model.

mdl = fitglm(pred,resp,'Distribution','binomial','Link','logit');

Compute the pointwise confidence intervals on the true positive rate (TPR) by vertical averaging (VA) and sampling using bootstrap.

[X,Y,T] = perfcurve(species(51:end,:),mdl.Fitted.Probability,...
       'virginica','NBoot',1000,'XVals',[0:0.05:1]);

'NBoot',1000 sets the number of bootstrap replicas to 1000. 'XVals','All' prompts perfcurve to return X, Y, and T values for all scores, and average the Y values (true positive rate) at all X values (false positive rate) using vertical averaging. If you do not specify XVals, then perfcurve computes the confidence bounds using threshold averaging by default.

Plot the pointwise confidence intervals.

errorbar(X,Y(:,1),Y(:,1)-Y(:,2),Y(:,3)-Y(:,1));
xlim([-0.02,1.02]); ylim([-0.02,1.02]);
xlabel('False positive rate') 
ylabel('True positive rate')
title('ROC Curve with Pointwise Confidence Bounds')
legend('PCBwVA','Location','Best')

Figure contains an axes object. The axes object with title ROC Curve with Pointwise Confidence Bounds, xlabel False positive rate, ylabel True positive rate contains an object of type errorbar. This object represents PCBwVA.

It might not always be possible to control the false positive rate (FPR, the X value in this example). So you might want to compute the pointwise confidence intervals on true positive rates (TPR) by threshold averaging.

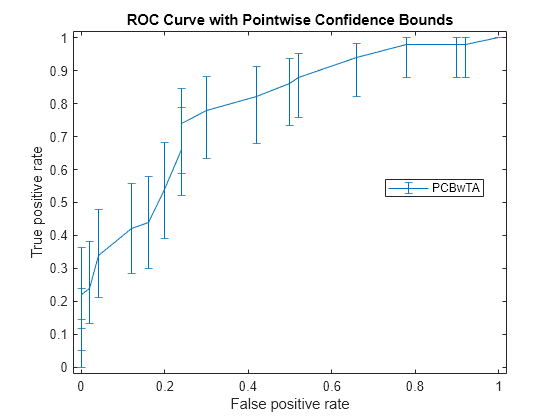
[X1,Y1,T1] = perfcurve(species(51:end,:),mdl.Fitted.Probability,...
    'virginica','NBoot',1000);

If you set 'TVals' to 'All', or if you do not specify 'TVals' or 'Xvals', then perfcurve returns X, Y, and T values for all scores and computes pointwise confidence bounds for X and Y using threshold averaging.

Plot the confidence bounds.

figure()
errorbar(X1(:,1),Y1(:,1),Y1(:,1)-Y1(:,2),Y1(:,3)-Y1(:,1));
xlim([-0.02,1.02]); ylim([-0.02,1.02]);
xlabel('False positive rate')
ylabel('True positive rate')
title('ROC Curve with Pointwise Confidence Bounds')
legend('PCBwTA','Location','Best')

Figure contains an axes object. The axes object with title ROC Curve with Pointwise Confidence Bounds, xlabel False positive rate, ylabel True positive rate contains an object of type errorbar. This object represents PCBwTA.

Specify the threshold values to fix and compute the ROC curve. Then plot the curve.

[X1,Y1,T1] = perfcurve(species(51:end,:),mdl.Fitted.Probability,...
    'virginica','NBoot',1000,'TVals',0:0.05:1);
figure()
errorbar(X1(:,1),Y1(:,1),Y1(:,1)-Y1(:,2),Y1(:,3)-Y1(:,1));
xlim([-0.02,1.02]); ylim([-0.02,1.02]);
xlabel('False positive rate')
ylabel('True positive rate')
title('ROC Curve with Pointwise Confidence Bounds')
legend('PCBwTA','Location','Best')

Figure contains an axes object. The axes object with title ROC Curve with Pointwise Confidence Bounds, xlabel False positive rate, ylabel True positive rate contains an object of type errorbar. This object represents PCBwTA.

Input Arguments

collapse all

True class labels, specified as a numeric vector, logical vector, character matrix, string array, categorical array, cell array of character vectors, or cell array. If labels is a cell array, it can contain elements with one of the other types. In this case, perfcurve uses cross-validation and treats each element of the cell array as a cross-validation fold. If scores is a cell array, labels must also be a cell array. labels and scores must contain the same number of elements. For more information, see Grouping Variables.

Example: {"hi","mid","hi","low",...,"mid"}

Example: ["H","M","H","L",...,"M"]

Data Types: single | double | logical | char | string | cell | categorical

Scores returned by a classifier for sample data, specified as a vector or cell array of floating points. scores must contain the same number of elements as labels. If labels is a cell array representing cross-validation folds, scores must also be a cell array.

Example: [0.82;0.60;0.79;0.16;…;0.71;0.48;0.63;0.53;0.35]

Data Types: single | double | cell

Positive class label, specified as a numeric scalar, logical scalar, character vector, string scalar, cell containing a character vector, or categorical scalar. The positive class must be a member of the input labels. The value of posclass that you can specify depends on the value of labels.

labels valueposclass value
Numeric vectorNumeric scalar
Logical vectorLogical scalar
Character matrixCharacter vector
String arrayString scalar
Cell array of character vectorsCharacter vector or cell containing character vector
Categorical vector Categorical scalar

For example, in a cancer diagnosis problem, if a malignant tumor is the positive class, then specify posclass as 'malignant'.

Data Types: single | double | logical | char | string | cell | categorical

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'NegClass','versicolor','XCrit','fn','NBoot',1000,'BootType','per' specifies the species versicolor as the negative class, the criterion for the X-coordinate as false negative, the number of bootstrap samples as 1000. It also specifies that the pointwise confidence bounds are computed using the percentile method.

List of negative classes, specified as the comma-separated pair consisting of 'NegClass', and a numeric array, a categorical array, a string array, or a cell array of character vectors. By default, perfcurve sets NegClass to 'all' and considers all nonpositive classes found in the input array of labels to be negative.

If NegClass is a subset of the classes found in the input array of labels, then perfcurve discards the instances with labels that do not belong to either positive or negative classes.

Example: 'NegClass',{'versicolor','setosa'}

Data Types: single | double | categorical | char | string | cell

Criterion to compute for X, specified as the comma-separated pair consisting of 'XCrit' and one of the following.

CriterionDescription
tpNumber of true positive instances.
fnNumber of false negative instances.
fpNumber of false positive instances.
tnNumber of true negative instances.
tp+fpSum of true positive and false positive instances.
rppRate of positive predictions.
rpp = (tp+fp)/(tp+fn+fp+tn)
rnpRate of negative predictions.
rnp = (tn+fn)/(tp+fn+fp+tn)
accuAccuracy.
accu = (tp+tn)/(tp+fn+fp+tn)
tpr, or sens, or recaTrue positive rate, or sensitivity, or recall.
tpr= sens = reca = tp/(tp+fn)
fnr, or miss False negative rate, or miss.
fnr = miss = fn/(tp+fn)
fpr, or fallFalse positive rate, or fallout, or 1 – specificity.
fpr = fall = fp/(tn+fp)
tnr, or specTrue negative rate, or specificity.
tnr = spec = tn/(tn+fp)
ppv, or precPositive predictive value, or precision.
ppv = prec = tp/(tp+fp)
npvNegative predictive value.
npv = tn/(tn+fn)
ecostExpected cost.
ecost = (tp*Cost(P|P)+fn*Cost(N|P)+fp* Cost(P|N)+tn*Cost(N|N))/(tp+fn+fp+tn)
Custom criterionA custom-defined function with the input arguments (C,scale,cost), where C is a 2-by-2 confusion matrix, scale is a 2-by-1 array of class scales, and cost is a 2-by-2 misclassification cost matrix.

Caution

Some of these criteria return NaN values at one of the two special thresholds, 'reject all' and 'accept all'.

Example: 'XCrit','ecost'

Criterion to compute for Y, specified as the comma-separated pair consisting of 'YCrit' and one of the same criteria options as for X. This criterion does not have to be a monotone function of the positive class score.

Example: 'YCrit','ecost'

Values for the X criterion, specified as the comma-separated pair consisting of 'XVals' and a numeric array.

  • If you specify XVals, then perfcurve computes X and Y and the pointwise confidence bounds for Y (when applicable) only for the specified XVals.

  • If you do not specify XVals, then perfcurve, computes X and Y and the values for all scores by default.

Note

You cannot set XVals and TVals at the same time.

Example: 'XVals',[0:0.05:1]

Data Types: single | double | char | string

Thresholds for the positive class score, specified as the comma-separated pair consisting of 'TVals' and either 'all' or a numeric array.

  • If TVals is set to 'all' or not specified, and XVals is not specified, then perfcurve returns X, Y, and T values for all scores and computes pointwise confidence bounds for X and Y using threshold averaging.

  • If TVals is set to a numeric array, then perfcurve returns X, Y, and T values for the specified thresholds and computes pointwise confidence bounds for X and Y at these thresholds using threshold averaging.

Note

You cannot set XVals and TVals at the same time.

Example: 'TVals',[0:0.05:1]

Data Types: single | double | char | string

Indicator to use the nearest values in the data instead of the specified numeric XVals or TVals, specified as the comma-separated pair consisting of 'UseNearest' and either 'on' or 'off'.

  • If you specify numeric XVals and set UseNearest to 'on', then perfcurve returns the nearest unique X values found in the data, and it returns the corresponding values of Y and T.

  • If you specify numeric XVals and set UseNearest to 'off', then perfcurve returns the sorted XVals.

  • If you compute confidence bounds by cross validation or bootstrap, then this parameter is always 'off'.

Example: 'UseNearest','off'

perfcurve method for processing NaN scores, specified as the comma-separated pair consisting of 'ProcessNaN' and 'ignore' or 'addtofalse'.

  • If ProcessNaN is 'ignore', then perfcurve removes observations with NaN scores from the data.

  • If ProcessNaN is 'addtofalse', then perfcurve adds instances with NaN scores to false classification counts in the respective class. That is, perfcurve always counts instances from the positive class as false negative (FN), and it always counts instances from the negative class as false positive (FP).

Example: 'ProcessNaN','addtofalse'

Prior probabilities for positive and negative classes, specified as the comma-separated pair consisting of 'Prior' and 'empirical', 'uniform', or an array with two elements.

If Prior is 'empirical', then perfcurve derives prior probabilities from class frequencies.

If Prior is 'uniform' , then perfcurve sets all prior probabilities to be equal.

Example: 'Prior',[0.3,0.7]

Data Types: single | double | char | string

Misclassification costs, specified as the comma-separated pair consisting of 'Cost' and a 2-by-2 matrix, containing [Cost(P|P),Cost(N|P);Cost(P|N),Cost(N|N)].

Cost(N|P) is the cost of misclassifying a positive class as a negative class. Cost(P|N) is the cost of misclassifying a negative class as a positive class. Usually, Cost(P|P) = 0 and Cost(N|N) = 0, but perfcurve allows you to specify nonzero costs for correct classification as well.

Example: 'Cost',[0 0.7;0.3 0]

Data Types: single | double

Significance level for the confidence bounds, specified as the comma-separated pair consisting of 'Alpha' and a scalar value in the range 0 through 1. perfcurve computes 100*(1 – α) percent pointwise confidence bounds for X, Y, T, and AUC for a confidence level of 1 – α.

Example: 'Alpha',0.01 specifies 99% confidence bounds.

Data Types: single | double

Observation weights, specified as the comma-separated pair consisting of 'Weights' and a vector of nonnegative scalar values. This vector must have as many elements as scores or labels do.

If scores and labels are in cell arrays and you need to supply Weights, the weights must be in a cell array as well. In this case, every element in Weights must be a numeric vector with as many elements as the corresponding element in scores. For example, numel(weights{1}) == numel(scores{1}).

When perfcurve computes the X, Y and T or confidence bounds using cross-validation, it uses these observation weights instead of observation counts.

When perfcurve computes confidence bounds using bootstrap, it samples N out of N observations with replacement, using these weights as multinomial sampling probabilities.

The default is a vector of 1s or a cell array in which each element is a vector of 1s.

Data Types: single | double | cell

Number of bootstrap replicas for computation of confidence bounds, specified as the comma-separated pair consisting of 'NBoot' and a positive integer. The default value 0 means the confidence bounds are not computed.

If labels and scores are cell arrays, this parameter must be 0 because perfcurve can use either cross-validation or bootstrap to compute confidence bounds.

Example: 'NBoot',500

Data Types: single | double

Confidence interval type for bootci to use to compute confidence intervals, specified as the comma-separated pair consisting of 'BootType' and one of the following:

  • 'bca' — Bias corrected and accelerated percentile method

  • 'norm or 'normal' — Normal approximated interval with bootstrapped bias and standard error

  • 'per' or 'percentile' — Percentile method

  • 'cper' or 'corrected percentile' — Bias corrected percentile method

  • 'stud' or 'student' — Studentized confidence interval

Example: 'BootType','cper'

Optional input arguments for bootci to compute confidence bounds, specified as the comma-separated pair consisting of 'BootArg' and {'Nbootstd',nbootstd}.

When you compute the studentized bootstrap confidence intervals ('BootType' is 'student'), you can additionally specify the 'Nbootstd' name-value pair argument of bootci by using 'BootArg'. For example, 'BootArg',{'Nbootstd',nbootstd} estimates the standard error of the bootstrap statistics using bootstrap with nbootstd data samples. nbootstd is a positive integer and its default is 100.

Example: 'BootArg',{'Nbootstd',nbootstd}

Data Types: cell

Options for controlling the computation of confidence intervals, specified as the comma-separated pair consisting of 'Options' and a structure array returned by statset. These options require Parallel Computing Toolbox™. perfcurve uses this argument for computing pointwise confidence bounds only. To compute these bounds, you must pass cell arrays for labels and scores or set NBoot to a positive integer.

This table summarizes the available options.

OptionDescription
'UseParallel'

  • false — Serial computation (default).

  • true — Parallel computation. You need Parallel Computing Toolbox for this option to work.

'UseSubstreams'

  • false — Do not use a separate substream for each iteration (default).

  • true — Use a separate substream for each iteration to compute in a reproducible fashion. To compute reproducibly, set Streams to a type allowing substreams: 'mlfg6331_64' or 'mrg32k3a'.

'Streams'

A RandStream object, or a cell array of such objects. If you specify Streams, use a single object, except when:

  • UseParallel is true.

  • UseSubstreams is false.

In that case, use a cell array of the same size as the parallel pool. If a parallel pool is not open, then Streams must supply a single random number stream.

If 'UseParallel' is true and 'UseSubstreams' is false, then the length of 'Streams' must equal the number of workers used by perfcurve. If a parallel pool is already open, then the length of 'Streams' is the size of the parallel pool. If a parallel pool is not already open, then MATLAB® might open a pool for you, depending on your installation and preferences. To ensure more predictable results, use parpool (Parallel Computing Toolbox) and explicitly create a parallel pool before invoking perfcurve and setting 'Options',statset('UseParallel',true).

Example: 'Options',statset('UseParallel',true)

Data Types: struct

Output Arguments

collapse all

x-coordinates for the performance curve, returned as a vector or an m-by-3 matrix. By default, X values are the false positive rate, FPR (fallout or 1 – specificity). To change X, use the XCrit name-value pair argument.

  • If perfcurve does not compute the pointwise confidence bounds, or if it computes them using vertical averaging, then X is a vector.

  • If perfcurve computes the confidence bounds using threshold averaging, then X is an m-by-3 matrix, where m is the number of fixed threshold values. The first column of X contains the mean value. The second and third columns contain the lower bound and the upper bound, respectively, of the pointwise confidence bounds.

y-coordinates for the performance curve, returned as a vector or an m-by-3 matrix. By default, Y values are the true positive rate, TPR (recall or sensitivity). To change Y, use YCrit name-value pair argument.

  • If perfcurve does not compute the pointwise confidence bounds, then Y is a vector.

  • If perfcurve computes the confidence bounds, then Y is an m-by-3 matrix, where m is the number of fixed X values or thresholds (T values). The first column of Y contains the mean value. The second and third columns contain the lower bound and the upper bound, respectively, of the pointwise confidence bounds.

Thresholds on classifier scores for the computed values of X and Y, returned as a vector or m-by-3 matrix.

  • If perfcurve does not compute the pointwise confidence bounds, or computes them using threshold averaging, then T is a vector.

  • If perfcurve computes the confidence bounds using vertical averaging, T is an m-by-3 matrix, where m is the number of fixed X values. The first column of T contains the mean value. The second and third columns contain the lower bound, and the upper bound, respectively, of the pointwise confidence bounds.

For each threshold, TP is the count of true positive observations with scores greater than or equal to this threshold, and FP is the count of false positive observations with scores greater than or equal to this threshold. perfcurve defines negative counts, TN and FN, in a similar way. The function then sorts the thresholds in the descending order that corresponds to the ascending order of positive counts.

For the m distinct thresholds found in the array of scores, perfcurve returns the X, Y and T arrays with m + 1 rows. perfcurve sets elements T(2:m+1) to the distinct thresholds, and T(1) replicates T(2). By convention, T(1) represents the highest 'reject all' threshold, and perfcurve computes the corresponding values of X and Y for TP = 0 and FP = 0. The T(end) value is the lowest 'accept all' threshold for which TN = 0 and FN = 0.

Area under the curve (AUC) for the computed values of X and Y, returned as a scalar value or a 3-by-1 vector.

  • If perfcurve does not compute the pointwise confidence bounds, AUC is a scalar value.

  • If perfcurve computes the confidence bounds using vertical averaging, AUC is a 3-by-1 vector. The first column of AUC contains the mean value. The second and third columns contain the lower bound and the upper bound, respectively, of the confidence bound.

For a perfect classifier, AUC = 1. For a classifier that randomly assigns observations to classes, AUC = 0.5.

If you set XVals to 'all' (default), then perfcurve computes AUC using the returned X and Y values.

If XVals is a numeric array, then perfcurve computes AUC using X and Y values from all distinct scores in the interval, which are specified by the smallest and largest elements of XVals. More precisely, perfcurve finds X values for all distinct thresholds as if XVals were set to 'all', and then uses a subset of these (with corresponding Y values) between min(XVals) and max(XVals) to compute AUC.

perfcurve uses trapezoidal approximation to estimate the area. If the first or last value of X or Y are NaNs, then perfcurve removes them to allow calculation of AUC. This takes care of criteria that produce NaNs for the special 'reject all' or 'accept all' thresholds, for example, positive predictive value (PPV) or negative predictive value (NPV).

Optimal operating point of the ROC curve, returned as a 1-by-2 array with false positive rate (FPR) and true positive rate (TPR) values for the optimal ROC operating point.

perfcurve computes OPTROCPT for the standard ROC curve only, and sets to NaNs otherwise. To obtain the optimal operating point for the ROC curve, perfcurve first finds the slope, S, using

S=Cost(P|N)−Cost(N|N)Cost(N|P)−Cost(P|P)*NP

  • Cost(N|P) is the cost of misclassifying a positive class as a negative class. Cost(P|N) is the cost of misclassifying a negative class as a positive class.

  • P = TP + FN and N = TN + FP. They are the total instance counts in the positive and negative class, respectively.

perfcurve then finds the optimal operating point by moving the straight line with slope S from the upper left corner of the ROC plot (FPR = 0, TPR = 1) down and to the right, until it intersects the ROC curve.

Values for negative subclasses, returned as an array.

  • If you specify only one negative class, then SUBY is identical to Y.

  • If you specify k negative classes, then SUBY is a matrix of size m-by-k, where m is the number of returned values for X and Y, and k is the number of negative classes. perfcurve computes Y values by summing counts over all negative classes.

SUBY gives values of the Y criterion for each negative class separately. For each negative class, perfcurve places a new column in SUBY and fills it with Y values for true negative (TN) and false positive (FP) counted just for this class.

Negative class names, returned as a cell array.

  • If you provide an input array of negative class names NegClass, then perfcurve copies names into SUBYNAMES.

  • If you do not provide NegClass, then perfcurve extracts SUBYNAMES from the input labels. The order of SUBYNAMES is the same as the order of columns in SUBY. That is, SUBY(:,1) is for negative class SUBYNAMES{1}, SUBY(:,2) is for negative class SUBYNAMES{2}, and so on.

Algorithms

collapse all

Pointwise Confidence Bounds

If you supply cell arrays for labels and scores, or if you set NBoot to a positive integer, then perfcurve returns pointwise confidence bounds for X,Y,T, and AUC. You cannot supply cell arrays for labels and scores and set NBoot to a positive integer at the same time.

perfcurve resamples data to compute confidence bounds using either cross validation or bootstrap.

  • Cross-validation — If you supply cell arrays for labels and scores, then perfcurve uses cross-validation and treats elements in the cell arrays as cross-validation folds. labels can be a cell array of numeric vectors, logical vectors, character matrices, cell arrays of character vectors, or categorical vectors. All elements in labels must have the same type. scores can be a cell array of numeric vectors. The cell arrays for labels and scores must have the same number of elements. The number of labels in cell j of labels must be equal to the number of scores in cell j of scores for any j in the range from 1 to the number of elements in scores.

  • Bootstrap — If you set NBoot to a positive integer n, perfcurve generates n bootstrap replicas to compute pointwise confidence bounds. If you use XCrit or YCrit to set the criterion for X or Y to an anonymous function, perfcurve can compute confidence bounds only using bootstrap.

perfcurve estimates the confidence bounds using one of two methods:

  • Vertical averaging (VA) — perfcurve estimates confidence bounds on Y and T at fixed values of X. That is, perfcurve takes samples of the ROC curves for fixed X values, averages the corresponding Y and T values, and computes the standard errors. You can use the XVals name-value pair argument to fix the X values for computing confidence bounds. If you do not specify XVals, then perfcurve computes the confidence bounds at all X values.

  • Threshold averaging (TA) — perfcurve takes samples of the ROC curves at fixed thresholds T for the positive class score, averages the corresponding X and Y values, and estimates the confidence bounds. You can use the TVals name-value pair argument to use this method for computing confidence bounds. If you set TVals to 'all' or do not specify TVals or XVals, then perfcurve returns X, Y, and T values for all scores and computes pointwise confidence bounds for Y and X using threshold averaging.

When you compute the confidence bounds, Y is an m-by-3 array, where m is the number of fixed X values or thresholds (T values). The first column of Y contains the mean value. The second and third columns contain the lower bound and the upper bound, respectively, of the pointwise confidence bounds. AUC is a row vector with three elements, following the same convention. If perfcurve computes the confidence bounds using VA, then T is an m-by-3 matrix, and X is a column vector. If perfcurve uses TA, then X is an m-by-3 matrix and T is a column-vector.

perfcurve returns pointwise confidence bounds. It does not return a simultaneous confidence band for the entire curve.

Alternative Functionality

  • You can compute the performance metrics for a ROC curve and other performance curves by creating a rocmetrics object. rocmetrics supports both binary and multiclass classification problems. You can pass classification scores returned by the predict function of a classification model object (such as predict of ClassificationTree) to rocmetrics without adjusting scores for a multiclass model.

    rocmetrics provides object functions to plot a ROC curve (plot), find an average ROC curve for multiclass problems (average), and compute additional metrics after creating an object (addMetrics). For more details, see the reference pages and ROC Curve and Performance Metrics.

References

[1] Fawcett, T. “ROC Graphs: Notes and Practical Considerations for Researchers”, Machine Learning 31, no. 1 (2004): 1–38.

[2] Zweig, M., and G. Campbell. “Receiver-Operating Characteristic (ROC) Plots: A Fundamental Evaluation Tool in Clinical Medicine.” Clinical Chemistry 39, no. 4 (1993): 561–577.

[3] Davis, J., and M. Goadrich. “The Relationship Between Precision-Recall and ROC Curves.” Proceedings of ICML ’06, 2006, pp. 233–240.

[4] Moskowitz, C. S., and M. S. Pepe. “Quantifying and Comparing the Predictive Accuracy of Continuous Prognostic Factors for Binary Outcomes.” Biostatistics 5, no. 1 (2004): 113–27.

[5] Huang, Y., M. S. Pepe, and Z. Feng. “Evaluating the Predictiveness of a Continuous Marker.” U. Washington Biostatistics Paper Series, 2006, 250–61.

[6] Briggs, W. M., and R. Zaretzki. “The Skill Plot: A Graphical Technique for Evaluating Continuous Diagnostic Tests.” Biometrics 64, no. 1 (2008): 250–256.

[7] Bettinger, R. “Cost-Sensitive Classifier Selection Using the ROC Convex Hull Method.” SAS Institute, 2003.

Extended Capabilities

Version History

Introduced in R2009a

expand all

See Also

| | | | | | |

Topics