Empirical Wavelet Transform

This example uses:

The empirical wavelet transform (EWT) is a technique that creates a multiresolution analysis (MRA) of a signal using an adaptive wavelet subdivision scheme. The EWT starts with a segmentation of the signal's spectrum. The EWT provides perfect reconstruction of the input signal. The EWT coefficients partition the energy of the input signal into separate passbands.

The EWT was developed by Gilles [1]. Gilles and Heal [3] proposed and use a histogram-based approach for segmenting the spectrum.

An MRA is a decomposition of a signal into components on different scales, or equivalently, on different frequency bands in such a way that the original signal is recovered by summing the components at each point in time (see Practical Introduction to Multiresolution Analysis). Many MRA techniques exist. The maximal overlap discrete wavelet transform (MODWT) and its associated MRA formulation use a basis or frame designed independently of the signal (see modwt and modwtmra). The empirical mode decomposition (EMD) algorithm is a data-adaptive technique that decomposes a nonlinear or nonstationary process into its intrinsic modes of oscillation. The EMD iterates on an input signal to extract natural AM-FM modes, also known as intrinsic mode functions, contained in the data (see emd).

EWT Algorithm

You can use the ewt function to obtain the MRA of a signal. The structure of the EWT algorithm is as follows.

We obtain a multitaper power spectral estimate of the signal using five sine tapers. This is a smooth, low-variance estimate of the power spectrum (see Bias and Variability in the Periodogram (Signal Processing Toolbox)). We normalize the estimate to lie in the range [0,1]. By default, we identify all peaks strictly greater than 70% of the peak value. If there is a dominant peak and many smaller ones, you can use the LogSpectrum option.
The empirical wavelet passbands are constructed by default, so that their transition bands cross at the geometric mean frequency of the adjacent peaks. The Meyer wavelets are constructed as described in [1] along with the way we determine the $γ$ parameter. The wavelets are overlapped in such a way that they form a Parseval tight frame.
For determining the boundaries between adjacent passbands, you have the option of using the first local minima between adjacent peaks. If no local minimum is identified, we revert to the geometric mean (default).
You also have the option to override the automatic thresholding of peaks using MaxNumPeaks. The largest peaks up to MaxNumPeaks are used. The approximate bandwidth of the multitaper estimate is (K+1/2)/(N+1), where K is the number of tapers, and N is the data length (which may include padding). Because peaks must be minimally separated by the approximate bandwidth to qualify as a peak, it is possible that fewer than MaxNumPeaks peaks, including no peaks, are identified.

Because the wavelets form a Parseval tight frame, the filter bank is self-dual: the analysis filter bank is equal to the synthesis filter bank. The EWT uses the wavelets to filter the signal in the frequency domain and then inverts the transform to obtain the analysis coefficients. The EWT uses the corresponding synthesis wavelets to reconstruct the MRA components.

Spectrum Segmentation

If you have Signal Processing Toolbox™, you can see how using multitapers can produce a smoothed estimate of the power spectrum.

Create the third test signal defined in [1] and add white noise. Set the random number generator to the default settings to produce repeatable results. Subtract its mean value and plot the result.

rng default
fs = 500;
t = 0:1/fs:1-1/fs;
f1 = 1./(6/5+cos(2*pi*t));
f2 = 1./(3/2+sin(2*pi*t));
f3 = cos(32*pi*t+cos(64*pi*t));
sig = f1+f2.*f3;
sig = sig+randn(1,length(sig))/2;
sig = sig-mean(sig);
plot(t,sig)
xlabel('Time (sec)')
ylabel('Amplitude')
title('Test Signal')

Figure contains an axes object. The axes object with title Test Signal, xlabel Time (sec), ylabel Amplitude contains an object of type line.

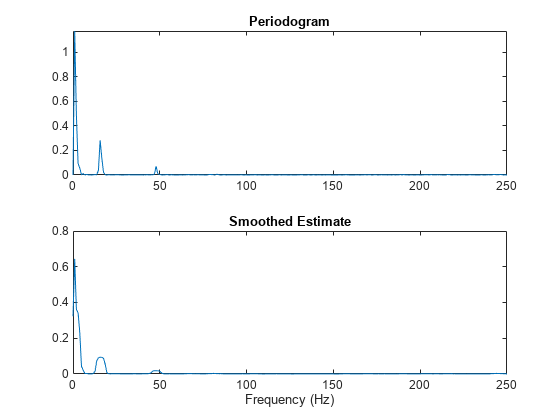
Use the periodogram function to plot the periodogram of the signal. Then use the pmtm function to plot the smoothed multitaper estimate.

[Pxx,F] = periodogram(sig,[],[],500);
Pxxmt = pmtm(sig,5,[],500,'Tapers','sine');
subplot(2,1,1)
plot(F,Pxx)
title('Periodogram')
subplot(2,1,2)
plot(F,Pxxmt)
title('Smoothed Estimate')
xlabel('Frequency (Hz)')

Figure contains 2 axes objects. Axes object 1 with title Periodogram contains an object of type line. Axes object 2 with title Smoothed Estimate, xlabel Frequency (Hz) contains an object of type line.

Computing EWT

You have several ways to control how the ewt function obtains the MRA of a signal. This section demonstrates a few options.

Use the ewt function with default settings to obtain the MRA of the signal and information about the filter bank.

[mra,~,~,info] = ewt(sig);
size(mra)

ans = 1×2

   500     2

Specify Peaks

By default, ewt finds two MRA components. Inspect the filter bank passbands. Because the passbands are returned in normalized frequencies, multiply them by the sampling frequency.

info.FilterBank.Passbands*fs

Note that there is a segment boundary at 22 Hz. The first segment has two peaks. Set MaxNumPeaks equal to 3 so that ewt determines the filter passbands using the three largest peaks.

[mra,cfs,~,info] = ewt(sig,'MaxNumPeaks',3);
info.FilterBank.Passbands*fs

ans = 3×2

   62.0000  250.0000
   28.0000   62.0000
         0   28.0000

Verify that summing the MRA components results in perfect reconstruction of the signal, and verify that the EWT analysis coefficients are energy preserving.

max(abs(sig'-sum(mra,2)))

ans = 
1.7764e-15

sum(sum(abs(cfs).^2))

ans = 
1.2985e+03

norm(sig,2)^2

ans = 
1.2985e+03

Instead of specifying a maximum number of peaks, you can set the percentage threshold used to determine which peaks are retained in the multitaper power spectrum. Local maxima in the multitaper power spectral estimate of the signal are normalized to lie in the range [0,1] with the maximum peak equal to 1. Set PeakThresholdPercent to 2.

[~,~,~,info] = ewt(sig,'PeakThresholdPercent',2);
info.FilterBank.Passbands*fs

ans = 5×2

  141.0000  250.0000
   74.0000  141.0000
   57.0000   74.0000
   28.0000   57.0000
         0   28.0000

Specify Segmentation Method

By default, ewt uses the geometric mean of adjacent peaks to determine the filter passbands. The ewt function gives you the option to instead use the first local minimum between peaks. Set SegmentMethod to 'localmin', so that ewt uses the first local minimum, and specify a maximum of three peaks. Confirm that using the first local minimum results in a different segmentation.

[~,~,~,info] = ewt(sig,'MaxNumPeaks',3,'SegmentMethod','localmin');
info.FilterBank.Passbands*fs

ans = 3×2

   54.0000  250.0000
   28.0000   54.0000
         0   28.0000

Specify Frequency Resolution

You can also specify the frequency resolution bandwidth of the multitaper power spectral estimate. The frequency resolution bandwidth determines how many sine tapers are used in the multitaper power spectrum estimate. Specify a frequency resolution of 0.2 and a maximum of three peaks. Note that even though MaxNumPeaks is set at 3, three peaks are not found using the specified frequency resolution.

[mra,~,~,info] = ewt(sig,'MaxNumPeaks',3,'FrequencyResolution',0.2);
info.FilterBank.Passbands*fs

ans = 2×2

   83.0000  250.0000
         0   83.0000

References

[1] Gilles, Jérôme. “Empirical Wavelet Transform.” IEEE Transactions on Signal Processing 61, no. 16 (August 2013): 3999–4010. https://doi.org/10.1109/TSP.2013.2265222.

[2] Gilles, Jérôme, Giang Tran, and Stanley Osher. “2D Empirical Transforms. Wavelets, Ridgelets, and Curvelets Revisited.” SIAM Journal on Imaging Sciences 7, no. 1 (January 2014): 157–86. https://doi.org/10.1137/130923774.

[3] Gilles, Jérôme, and Kathryn Heal. “A Parameterless Scale-Space Approach to Find Meaningful Modes in Histograms — Application to Image and Spectrum Segmentation.” International Journal of Wavelets, Multiresolution and Information Processing 12, no. 06 (November 2014): 1450044. https://doi.org/10.1142/S0219691314500441.