Main Content

Signal Multiresolution Analyzer

Decompose signals into time-aligned components

expand all in page

Description

The Signal Multiresolution Analyzer app is an interactive tool for visualizing multilevel wavelet- and data adaptive-based decompositions of real-valued 1-D signals and comparing results. The app supports single- and double-precision data. With the app, you can:

  • Access all the real-valued 1-D signals in your MATLAB® workspace.

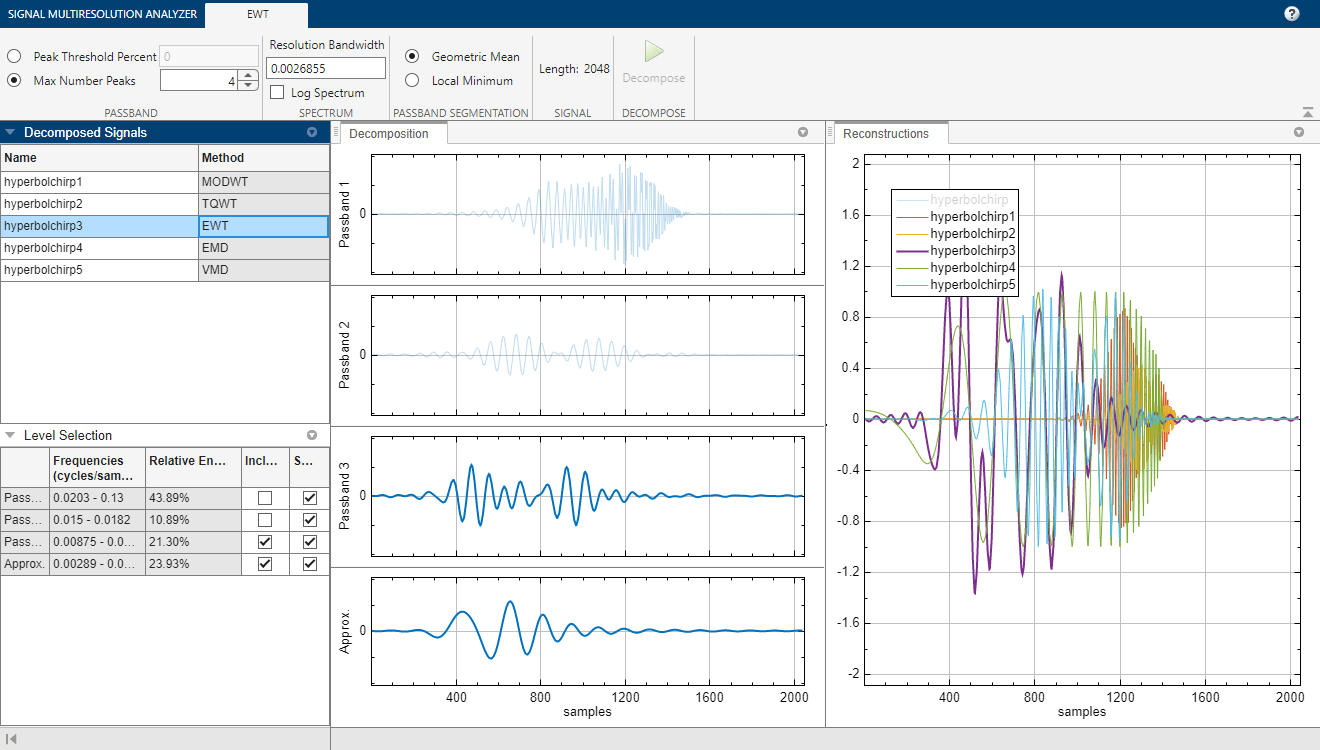
  • Generate decompositions using fixed-bandwidth and data-adaptive multiresolution analysis (MRA) methods:

    • Fixed-bandwidth: Maximal overlap discrete wavelet transform (MODWT) (default), and tunable Q-factor wavelet transform (TQWT)

    • Data-adaptive: Empirical mode decomposition (EMD), empirical wavelet transform (EWT), and variational mode decomposition (VMD)

  • Adjust default parameters, and visualize and compare multiple decompositions.

  • Choose decomposition levels to include in the signal reconstruction.

  • Obtain frequency ranges of the decomposition levels.

  • Determine the relative energy of the signal across levels.

  • Export reconstructed signals and decompositions to your workspace.

  • Recreate decompositions in your workspace by generating MATLAB scripts.

Signal Multiresolution Analyzer app

Open the Signal Multiresolution Analyzer App

  • MATLAB Toolstrip: On the Apps tab, under Signal Processing and Communications, click the app icon.

  • MATLAB command prompt: Enter signalMultiresolutionAnalyzer.

Examples

Parameters

expand all

Orthogonal wavelet family to use to generate the multiresolution analysis (default), specified as:

  • sym — Symlets

  • coif — Coiflets

  • db — Daubechies wavelets

  • fk — Fejér-Korovkin wavelets

The Wavelet parameter is applicable only for generating a multiresolution analysis.

For more information about the wavelets, use the waveinfo function. For example, to learn more about Daubechies wavelets, enter waveinfo('db').

Interpolation method to use for envelope construction in empirical mode decomposition, specified as one of the following:

  • spline — Cubic spline interpolation

  • pchip — Piecewise cubic Hermite interpolating polynomial method

The Interpolation parameter is applicable only for generating an empirical mode decomposition. You can change other options with the app when creating empirical mode decompositions. For more information, see emd.

Programmatic Use

expand all

signalMultiresolutionAnalyzer opens the Signal Multiresolution Analyzer app. Once the app initializes, import a signal for analysis by clicking Import.

signalMultiresolutionAnalyzer(sig) opens the Signal Multiresolution Analyzer app and imports, decomposes, and plots the multiresolution analysis of sig using modwtmra and modwt with the sym4 wavelet and default settings.

sig is a variable in the workspace. sig can be:

  • A 1-by-N or N-by-1 real-valued vector.

  • Single- or double-precision data.

By default, the app plots the decomposition levels as functions of sample index. To plot with respect to time, you can set a sample rate or sample period using the app.

Tips

  • To decompose one channel of a multichannel signal, import the channel programmatically. For example, decompose the 10th channel of the multichannel Espiga3 EEG data set using these commands.

    load Espiga3
signalMultiresolutionAnalyzer(Espiga3(:,10))

  • To decompose different 1-D signals simultaneously, run multiple instances of Signal Multiresolution Analyzer.

  • For the MODWT and TQWT decomposition methods, the script generated by Signal Multiresolution Analyzer supports gpuArray (Parallel Computing Toolbox) inputs.

Algorithms

expand all

References

[1] Percival, Donald B., and Andrew T. Walden. Wavelet Methods for Time Series Analysis. Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge ; New York: Cambridge University Press, 2000.

Version History

Introduced in R2018b

expand all

See Also

Apps

Functions

Topics