Main Content

Wavelet Time-Frequency Analyzer

Visualize scalogram of signals

Since R2022a

expand all in page

Description

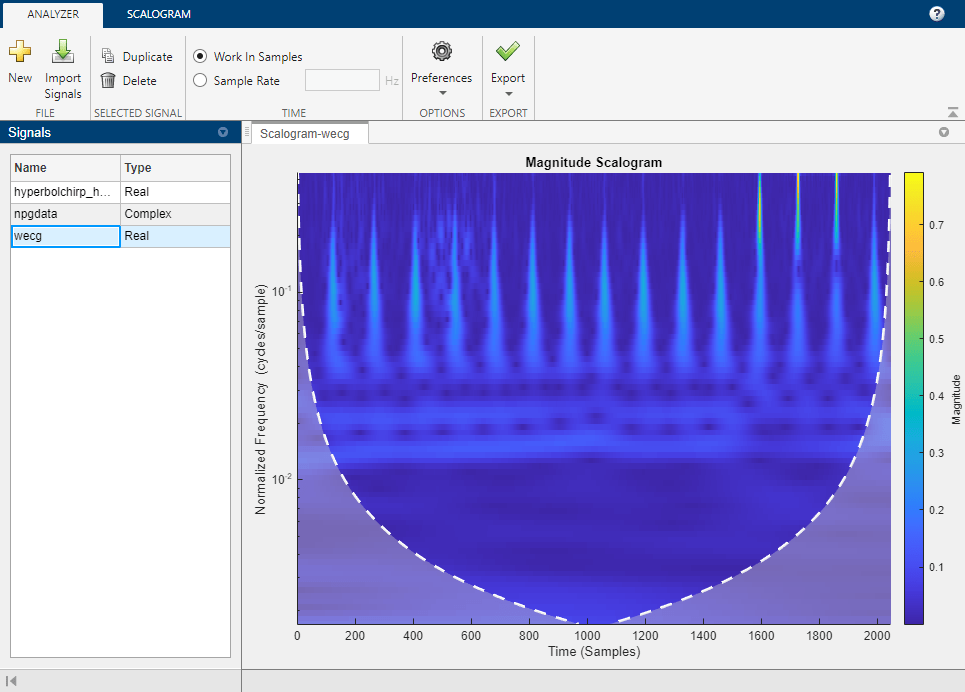
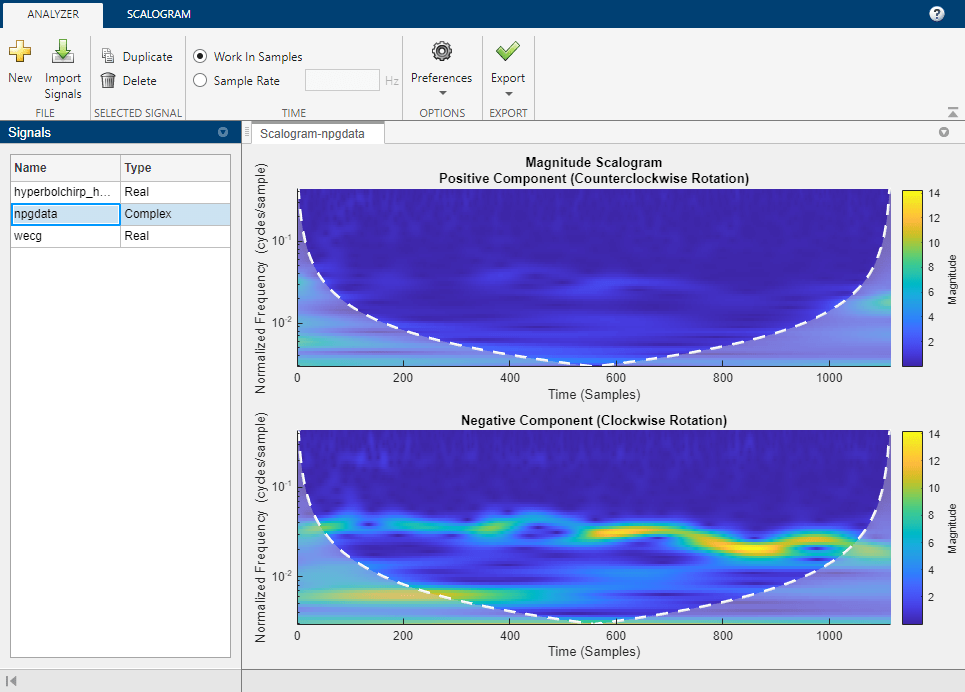
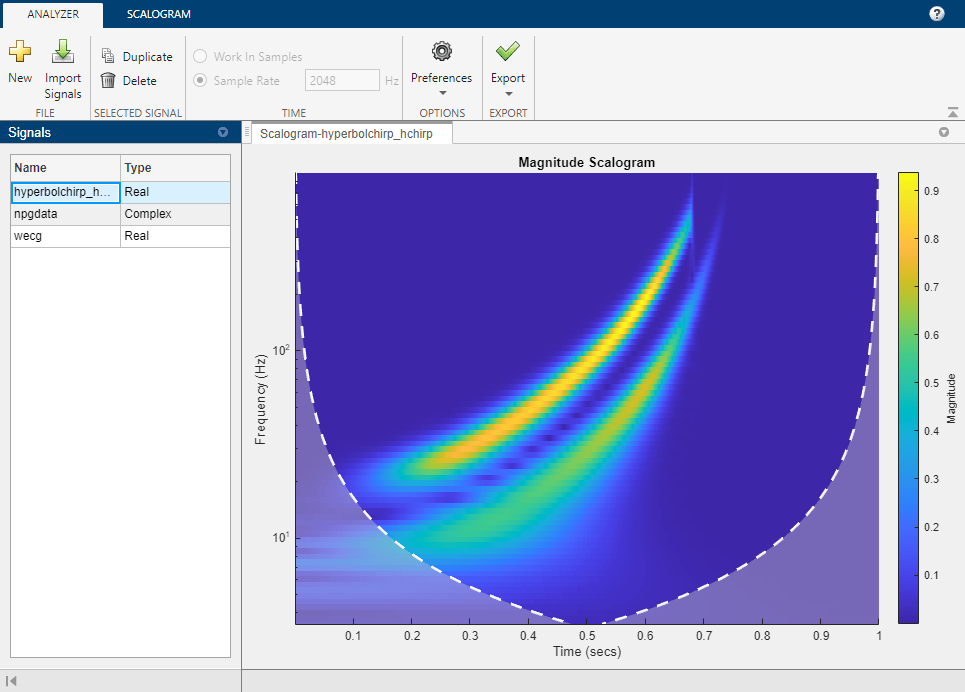
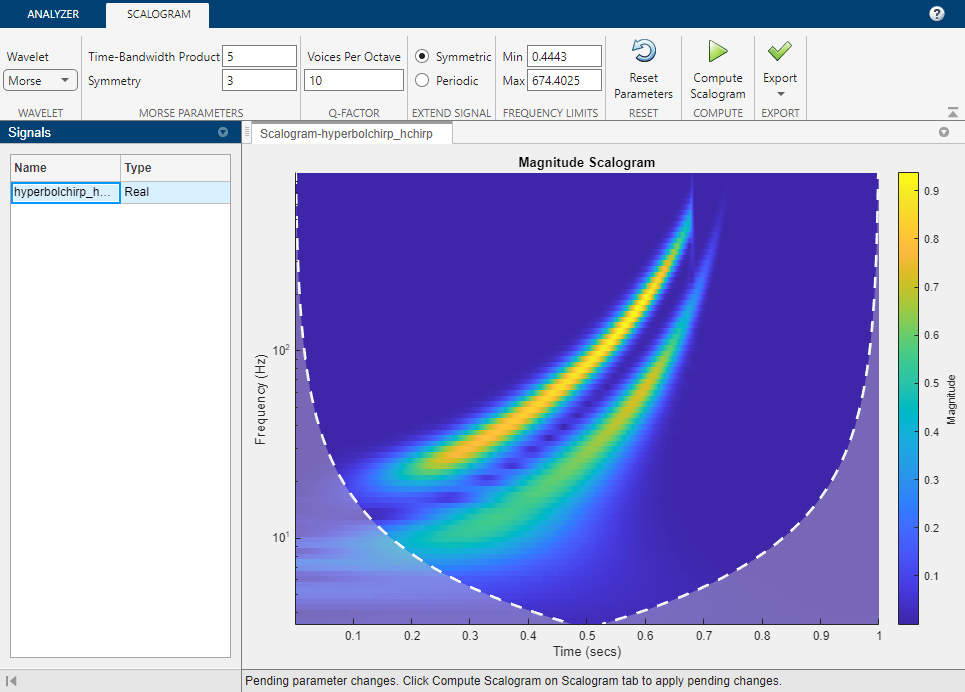
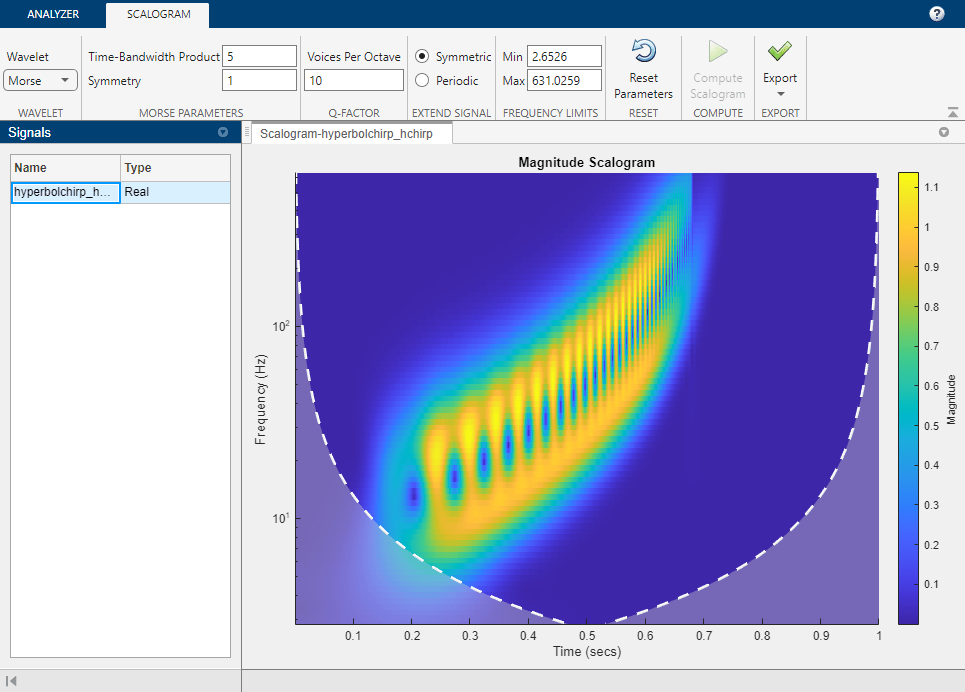
The Wavelet Time-Frequency Analyzer app is an interactive tool for visualizing scalograms of real- and complex-valued 1-D signals. The scalogram is the absolute value of the continuous wavelet transform (CWT) plotted as a function of time and frequency. Frequency is plotted on a logarithmic scale. With the app, you can:

  • Access all 1-D signals in your MATLAB® workspace

  • Import multiple signals simultaneously

  • Adjust default parameters and visualize scalograms using cwt

  • Select desired analytic wavelet

  • Adjust analytic Morse wavelet symmetry and time-bandwidth parameters

  • Export the CWT to your workspace

  • Recreate the scalogram in your workspace by generating a MATLAB script

  • Import multiple signals

For more information, see Using Wavelet Time-Frequency Analyzer App.

Wavelet Time-Frequency Analyzer app

Open the Wavelet Time-Frequency Analyzer App

  • MATLAB Toolstrip: On the Apps tab, under Signal Processing and Communications, click the app icon.

  • MATLAB command prompt: Enter waveletTimeFrequencyAnalyzer.

Examples

expand all

Open Live Script

Load three 1-D signals into the MATLAB® workspace: an electrocardiogram signal, a hyperbolic chirp signal, and the NPG2006 dataset.

load wecg
load hyperbolchirp
load npg2006

Extract the complex-valued signal from the npg2006 structure array.

npgdata = npg2006.cx;
whos
  Name                  Size            Bytes  Class        Attributes

  hyperbolchirp      2048x1             33759  timetable              
  npg2006               1x1             36991  struct                 
  npgdata            1117x1             17872  double       complex   
  wecg               2048x1             16384  double

Open Wavelet Time-Frequency Analyzer and click Import Signals. A window appears listing all the workspace variables the app can process.

importSignals.png

Select all the signals and click Import. After a brief, one-time initialization, the Signals pane is populated with the names of the imported signals, along with their types. In the case of hyperbolchirp, the name of the timetable variable containing the signal is appended to the name of the timetable: hyperbolchirp_hchirp. The app displays the scalogram of the highlighted signal. The scalogram is obtained using the cwt function with default settings. The cone of influence showing where edge effects become significant is also plotted. Gray regions outside the dashed white lines delineate regions where edge effects are significant. By default, frequencies are in cycles/sample.

screenshot1.png

The ECG signal is real valued. In the Signals pane, select the complex-valued signal npgdata. The positive and negative components of the scalogram are displayed.

screenshot3.png

Select hyperbolchirp_hchirp. Because the timetable contains temporal information, the scalogram is plotted as a function of frequency in hertz and uses the row times of the timetable as the basis for the time axis. The disabled Sample Rate field displays the sampling rate as determined from the row times.

timetableScalo.png

Open Live Script

Load the hyperbolic chirp signal.

load hyperbolchirp

Open Wavelet Time-Frequency Analyzer and import the signal into the app. To access the parameter settings, click the Scalogram tab. By default, the app displays the scalogram obtained using the analytic Morse (3, 60) wavelet and the cwt function with default settings.

You can reset the CWT parameters to their default values at any time by clicking Reset Parameters. Resetting the parameters enables the Compute Scalogram button.

screenshot4.png

To visualize the scalogram using the (1,5) Morse wavelet, set Time-Bandwidth Product to 5. In the status bar, text appears stating there are pending changes. The Compute Scalogram button is now enabled. If you instead first set Symmetry to 1, the app would automatically change that value because a symmetry value of 1 violates the constraint that the ratio of Time-Bandwidth Product to Symmetry should not exceed 40. For more information, see Tips.

screenshot5.png

Now set Symmetry to 1 and click Compute Scalogram. The app displays the scalogram obtained using the (1, 5) Morse wavelet.

screenshot7.png

To visualize the scalogram using the (6, 50) Morse wavelet, first set Time-Bandwidth Product to 50 and Symmetry to 6, then click Compute Scalogram.

Open Live Script

Import Signal

Load a hyperbolic chirp signal into your workspace.

load hyperbolchirp

Visualize Scalogram

Open Wavelet Time-Frequency Analyzer and import the signal. To access the parameter settings, click the Scalogram tab. By default, the app displays the scalogram obtained using the Morse (3,60) wavelet and the cwt function with default settings. Because the signal is a timetable, the scalogram is plotted as a function of frequency in hertz. The time axis is based on the row times of the timetable.

In the Scalogram tab, adjust the default settings. Specify the Morse (5,20) wavelet. Visualize the scalogram using 26 voices per octave and periodic boundary extension. The frequencies are plotted on a logarithmic scale.

2021-11-04_15-22-25.png

Generate Script

To adjust the frequency axis scale in the scalogram, first reproduce the wavelet analysis in your workspace.

Generate a script that recreates the scalogram in your workspace. From the Export ▼ menu, select Generate MATLAB Script. An untitled script opens in your MATLAB® Editor. To include the boundary line of the cone of influence in the plot, add a third output argument, coi, to the cwt function call in the script. Save and execute the script. The variables scalogram and frequency contain the scalogram and frequency vector, respectively.

%Parameters
waveletParameters = [5,20];
voicesPerOctave = 26;
extendSignal = false;

%Compute cwt
%Run the function call below without output arguments to plot the results
[waveletTransform,frequency,coi] = cwt(hyperbolchirp,...
    WaveletParameters = waveletParameters,...
    VoicesPerOctave = voicesPerOctave,...
    ExtendSignal = extendSignal);
scalogram = abs(waveletTransform);

In order to plot the scalogram using the correct time axis, extract the vector of row times, Time, from the hyperbolchirp timetable.

dataTimes = hyperbolchirp.Time;

Adjust Frequency Axis — Linear Scale

Use the pcolor function to plot the scalogram. Include the cone of influence boundary. Frequency is plotted on a linear scale.

pcolor(dataTimes,frequency,scalogram)
shading flat
title("Scalogram")
xlabel("Time (s)")
ylabel("Frequency (Hz)")
hold on
plot(dataTimes,coi,"w--",LineWidth=2)
hold off
colorbar

Figure contains an axes object. The axes object with title Scalogram, xlabel Time (s), ylabel Frequency (Hz) contains 2 objects of type surface, line.

Adjust Frequency Axis — Logarithmic Scale

To plot frequency on a logarithmic scale, get the handle to the current axes and set YScale to "log".

AX = gca;
set(AX,YScale="log")

Figure contains an axes object. The axes object with title Scalogram, xlabel Time (s), ylabel Frequency (Hz) contains 2 objects of type surface, line.

In MATLAB, logarithmic axes are in powers of 10 (decades). By default, MATLAB places frequency ticks at 1, 10, and 100 because they are the powers of 10 between the minimum and maximum frequencies. To add more frequency axis ticks, obtain the minimum and maximum frequencies in frequency. Create a logarithmically spaced set of frequencies between the minimum and maximum frequencies. Note that cwt returns frequencies ordered from high to low.

minf = frequency(end);
maxf = frequency(1);
numfreq = 10;
freq = logspace(log10(minf),log10(maxf),numfreq);

Replace the frequency axis ticks and labels with the new frequencies.

AX.YTickLabelMode = "auto";
AX.YTick = freq;

Figure contains an axes object. The axes object with title Scalogram, xlabel Time (s), ylabel Frequency (Hz) contains 2 objects of type surface, line.

In the CWT, frequencies are computed in powers of two. Create the frequency ticks and tick labels in powers of two.

freq = 2.^(round(log2(minf)):round(log2(maxf)));
AX.YTickLabelMode = "auto";
AX.YTick = freq;

Figure contains an axes object. The axes object with title Scalogram, xlabel Time (s), ylabel Frequency (Hz) contains 2 objects of type surface, line.

Related Examples

Parameters

expand all

Analytic wavelet used to compute the CWT. Valid options are Morse, Morlet, and bump, which specify the Morse, Morlet (Gabor), and bump wavelet, respectively.

Specify the time-bandwidth product of the Morse wavelet as a scalar greater than or equal to the Symmetry value. The ratio of the Time-Bandwidth Product value to the Symmetry value cannot exceed 40.

The values of Time-Bandwidth Product and Symmetry correspond to the WaveletParameters name-value argument of cwt.

Example: Setting Time-Bandwidth Product to 40 and Symmetry value to 5 is equivalent to setting the WaveletParameters name-value argument cwt(…,WaveletParameters=[5 40],…).

Specify the symmetry parameter of the Morse wavelet as a scalar greater than or equal to 1. The ratio of the Time-Bandwidth Product value to the Symmetry value cannot exceed 40.

The values of Symmetry and Time-Bandwidth Product correspond to the WaveletParameters name-value argument of cwt.

Specify the number of voices per octave to use for the CWT as an integer from 1 to 48. The CWT scales are discretized using the specified number of voices per octave. The energy spread of the wavelet in frequency and time automatically determines the minimum and maximum scales.

Programmatic Use

expand all

waveletTimeFrequencyAnalyzer opens the Wavelet Time-Frequency Analyzer app. Once the app initializes, import a signal for analysis by clicking Import Signals.

waveletTimeFrequencyAnalyzer(sig) opens the Wavelet Time-Frequency Analyzer app and imports, generates, and plots the scalogram of sig using cwt with default settings.

sig is a variable in the workspace. sig can be:

  • A real- or complex-valued vector.

  • A single-variable regularly sampled timetable.

  • Single- or double-precision data.

sig must have at least four samples.

By default, the app plots the scalogram as a function of frequency in cycles/sample and uses sample index as the basis of the time axis. If the signal is a timetable, then the app plots the scalogram as a function of frequency in hertz and uses the row times of the timetable as the basis for the time axis.

Limitations

  • The MATLAB script you generate to create the scalogram in your workspace uses the name of the selected signal in the Signals pane. The script will throw an error if the variable does not exist in the MATLAB workspace. If an error occurs, either replace the variable name in the script with the name of the original signal or create the variable in your workspace.

  • You can run only one instance of the Wavelet Time-Frequency Analyzer app in a MATLAB session.

Tips

  • The Morse wavelet parameters, Time-Bandwidth Product and Symmetry, must satisfy three constraints:

    • Symmetry, or gamma, must be greater than or equal to 1.

    • Time-Bandwidth Product must be greater than or equal to Symmetry.

    • The ratio of Time-Bandwidth Product to Symmetry cannot exceed 40.

    To prevent attempts to visualize a scalogram using invalid settings, the app validates any parameter you change. If you enter a value that violates a constraint, the app automatically replaces it with a valid value. The new value might not be the desired value. To avoid unexpected results, you should ensure any value you enter always results in a valid setting. For more information, see the example Adjust Morse Wavelet Parameters.

Version History

Introduced in R2022a

See Also

Apps

Functions

Topics