Fault Detection Using Wavelet Scattering and Recurrent Deep Networks
This example shows how to classify faults in acoustic recordings of air compressors using a wavelet scattering network paired with a recurrent neural network. The example provides the opportunity to use a GPU to accelerate the computation of the wavelet scattering transform. If you wish to utilize a GPU, you must have Parallel Computing Toolbox™ and a supported GPU. See GPU Computing Requirements (Parallel Computing Toolbox) for details.
Data Set
The data set consists of acoustic recordings collected on a single stage reciprocating type air compressor [1]. The data are sampled at 16 kHz. Specifications of the air compressor are as follows:
Air Pressure Range: 0-500 lb/m2, 0-35 Kg/cm2
Induction Motor: 5HP, 415V, 5Am, 50 Hz, 1440rpm
Pressure Switch: Type PR-15, Range 100-213 PSI
Each recording represents one of eight states: the healthy state and seven faulty states. The seven faulty states are:
Leakage inlet valve (LIV) fault
Leakage outlet valve (LOV) fault
Non-return valve (NRV) fault
Piston ring fault
Flywheel fault
Rider belt fault
Bearing fault
Download the data set and unzip the data file in a folder where you have write permission. This example assumes you download the data in the temporary directory designated as tempdir in MATLAB®. If you choose to use a different folder, substitute that folder for tempdir in the following. The recordings are stored as WAV files in folders named for their respective state.
url = "https://www.mathworks.com/supportfiles/audio/AirCompressorDataset/AirCompressorDataset.zip"; downloadFolder = fullfile(tempdir,"AirCompressorDataSet"); if ~exist(fullfile(tempdir,"AirCompressorDataSet"),"dir") loc = websave(downloadFolder,url); unzip(loc,fullfile(tempdir,"AirCompressorDataSet")) end
Use an audioDatastore to manage data access. Each subfolder contains only recordings of the designated class. Use the folder names as the class labels.
datasetLocation = fullfile(tempdir,"AirCompressorDataSet","AirCompressorDataset"); ads = audioDatastore(datasetLocation,IncludeSubfolders=true, ... LabelSource="foldernames");
Examine the number of recordings in each class. There are 225 recordings in each class.
countcats(ads.Labels)
ans = 8×1
225
225
225
225
225
225
225
225
Split the data into training and test sets. Use 80% of the data for training and hold out the remaining 20% for testing. Shuffle the data once before splitting.
rng default
ads = shuffle(ads);
[adsTrain,adsTest] = splitEachLabel(ads,0.8,0.2);Verify that the number of recordings in each class is the expected number.
uniqueLabels = unique(adsTrain.Labels); tblTrain = countEachLabel(adsTrain); tblTest = countEachLabel(adsTest); H = bar(uniqueLabels,[tblTrain.Count, tblTest.Count],"stacked"); legend(H,["Training Set","Test Set"],Location="NorthEastOutside")

Select eight random recordings from the training set and plot them.
idx = randperm(numel(adsTrain.Files),8); Fs = 16e3; tiledlayout(4,2) for n = 1:numel(idx) x = audioread(adsTrain.Files{idx(n)}); t = (0:size(x,1)-1)/Fs; nexttile plot(t,x) if n == 7 || n == 8 xlabel("Seconds") end title(string(adsTrain.Labels(idx(n)))) end

Wavelet Scattering Network
Each recording has 50,000 samples. The sample rate is 16 kHz. Construct a wavelet scattering network based on the data characteristics. Set the invariance scale to be 0.5 seconds.
N = 5e4;
Fs = 16e3;
IS = 0.5;
sn = waveletScattering(SignalLength=N,SamplingFrequency=Fs, ...
InvarianceScale=IS);With these network settings, there are 330 scattering paths and 25 time windows per recording. You can see this with the following code.
[~,npaths] = paths(sn); Ncfs = numCoefficients(sn); sum(npaths)
ans = 330
Ncfs
Ncfs = 25
Note this already represents a 6-fold reduction in the size of the data for each record. We reduced the data size from 50,000 samples to 8250 in total. Most importantly, we reduced the size of the data along the time dimension from 50,000 to 25 samples. This is crucial for our use of a recurrent network. Attempting to use a recurrent network on the original data with 50,000 samples would immediately result in memory problems.
Obtain the wavelet scattering features for the training and test sets. If you have a suitable GPU and Parallel Computing Toolbox, you can set useGPU to true to accelerate the scattering transform. The function helperBatchScatFeatures obtains the scattering transform of each example.
batchsize = 64; useGPU = false; scTrain = []; while hasdata(adsTrain) sc = helperBatchScatFeatures(adsTrain,sn,N,batchsize,useGPU); scTrain = cat(3,scTrain,sc); end
Repeat the process for the held-out test set.
scTest = []; while hasdata(adsTest) sc = helperBatchScatFeatures(adsTest,sn,N,batchsize,useGPU); scTest = cat(3,scTest,sc); end
Remove the 0-th order scattering coefficients. For both the training and test sets, put each 330-by-25 scattering transform into an element of a cell array for use in training and testing the recurrent network.
TrainFeatures = scTrain(2:end,:,:); TrainFeatures = squeeze(num2cell(TrainFeatures,[1 2])); YTrain = adsTrain.Labels; TestFeatures = scTest(2:end,:,:); TestFeatures = squeeze(num2cell(TestFeatures,[1 2])); YTest = adsTest.Labels;
Define Network
Recall there are 1440 training examples and 360 test set examples. Accordingly the TrainFeatures and TestFeatures cell arrays have 1440 and 360 elements respectively.
Use the number of scattering paths as the number of features. Create a recurrent network with a single LSTM layer having 512 hidden units. Follow the LSTM layer with a fully connected layer and finally a softmax layer. Use "zscore" normalization across all scattering paths at the input to the network.
[inputSize, ~] = size(TrainFeatures{1});
numHiddenUnits = 512;
numClasses = numel(unique(YTrain));
layers = [ ...
sequenceInputLayer(inputSize,Normalization="zscore")
lstmLayer(numHiddenUnits,OutputMode="last")
fullyConnectedLayer(numClasses)
softmaxLayer
];Train Network
Train the network for 50 epochs with a mini batch size of 128. Use an Adam optimizer with an initial learn rate of 1e-4. Shuffle the data each epoch. Because the training data has sequences with rows and columns corresponding to channels and time steps, respectively, specify the input data format "CTB" (channel, time, batch).
maxEpochs = 50; miniBatchSize = 128; options = trainingOptions("adam", ... InitialLearnRate=1e-4, ... MaxEpochs=maxEpochs, ... MiniBatchSize=miniBatchSize, ... SequenceLength="shortest", ... Shuffle="every-epoch", ... Plots="training-progress", ... Metrics="accuracy", ... Verbose=true, ... InputDataFormats="CTB"); net = trainnet(TrainFeatures,YTrain,layers,"crossentropy",options);
Iteration Epoch TimeElapsed LearnRate TrainingLoss TrainingAccuracy
_________ _____ ___________ _________ ____________ ________________
1 1 00:00:01 0.0001 2.1179 15.625
50 5 00:00:19 0.0001 0.063527 100
100 10 00:00:28 0.0001 0.0088835 100
150 14 00:00:37 0.0001 0.0028484 100
200 19 00:00:47 0.0001 0.0020476 100
250 23 00:00:57 0.0001 0.0014522 100
300 28 00:01:08 0.0001 0.00099056 100
350 32 00:01:16 0.0001 0.00090123 100
400 37 00:01:27 0.0001 0.00065444 100
450 41 00:01:38 0.0001 0.00050745 100
500 46 00:01:49 0.0001 0.00057337 100
550 50 00:01:58 0.0001 0.00055174 100
Training stopped: Max epochs completed
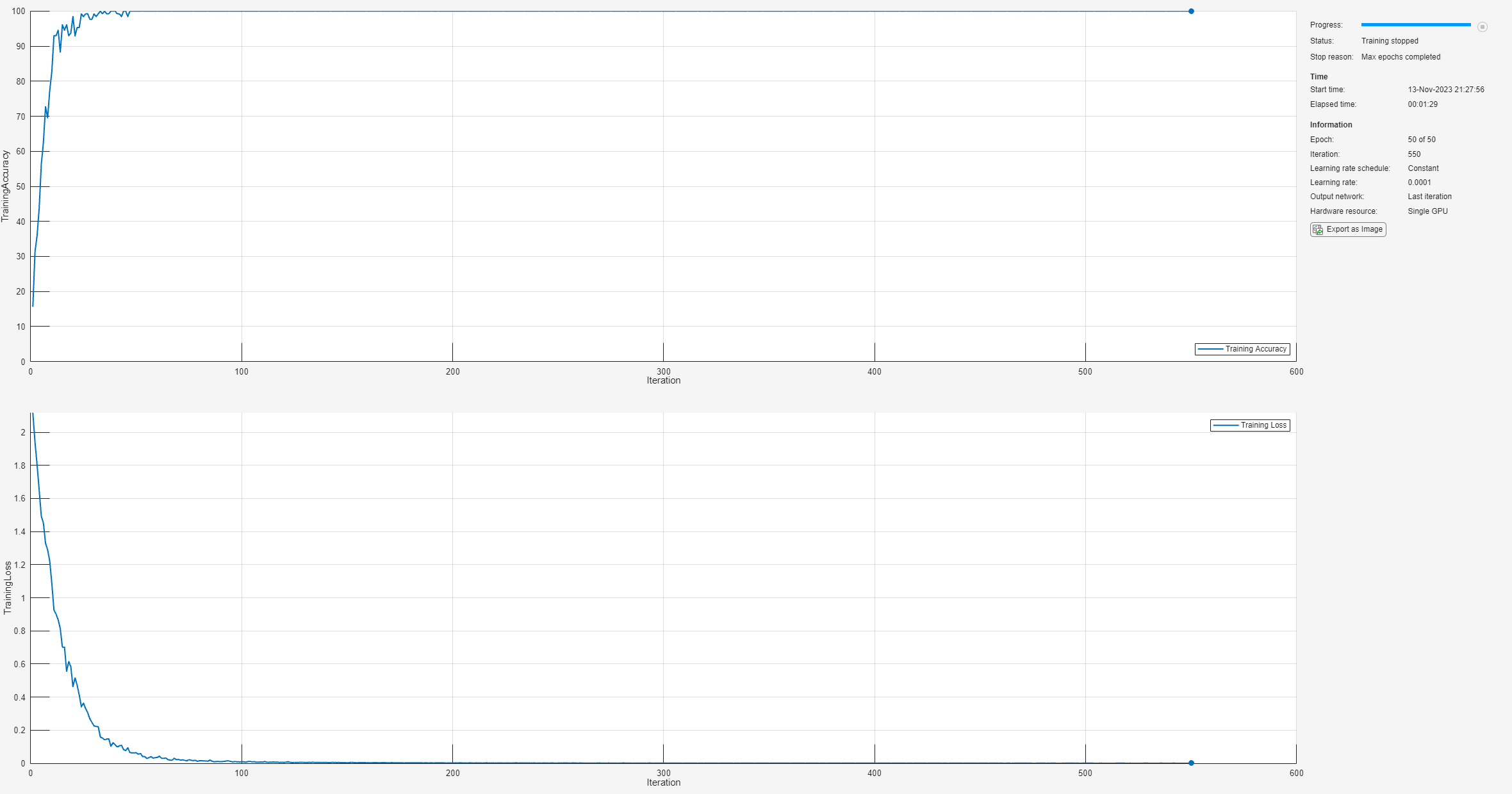
In training, the network has achieved near perfect performance. In order to ensure we have not overfit to the training data, use the held-out test set to determine how well our network generalizes to unseen data.
scores = minibatchpredict(net,TestFeatures,InputDataFormats="CTB");
classNames = categories(YTrain);
YPred = scores2label(scores,classNames);
accuracy = 100*sum(YPred == YTest) / numel(YTest)accuracy = 100
In this case, we see that the performance on the held-out test set is also excellent.
figure confusionchart(YTest, YPred)
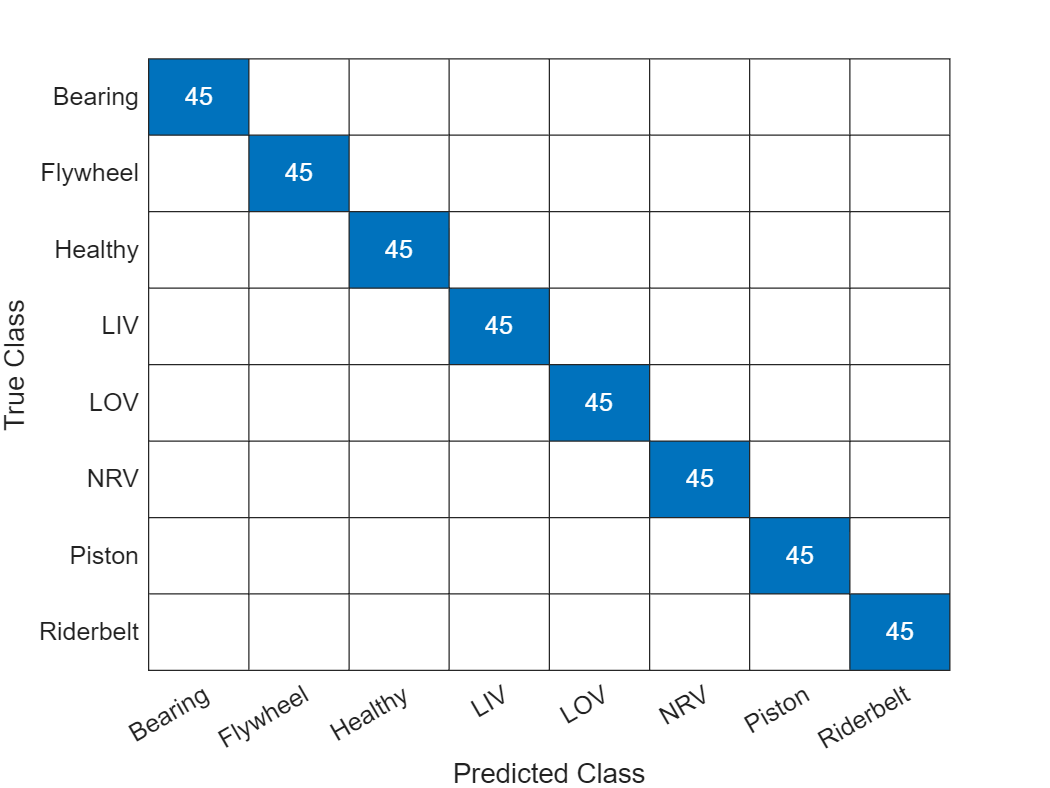
Summary
In this example, the wavelet scattering transform was used with a simple recurrent network to classify faults in an air compressor. The scattering transform allowed us to extract robust features for our learning problem. Additionally, the data reduction achieved along the time dimension of the data by the use of the wavelet scattering transform was critical in order to create a computationally feasible problem for our recurrent network.
References
[1] Verma, Nishchal K., Rahul Kumar Sevakula, Sonal Dixit, and Al Salour. “Intelligent Condition Based Monitoring Using Acoustic Signals for Air Compressors.” IEEE Transactions on Reliability 65, no. 1 (March 2016): 291–309. https://doi.org/10.1109/TR.2015.2459684.
helperbatchscatfeatures - This function returns the wavelet time scattering feature matrix for a given input signal. If useGPU is set to true, the scattering transform is computed on the GPU.
function S = helperBatchScatFeatures(ds,sn,N,batchsize,useGPU) % This function is only intended to support examples in the Wavelet % Toolbox. It may be changed or removed in a future release. % Read batch of data from audio datastore batch = helperReadBatch(ds,N,batchsize); if useGPU batch = gpuArray(batch); end % Obtain scattering features S = featureMatrix(sn,batch,Transform="log"); S = gather(S); end
helperReadBatch - This function reads batches of a specified size from a datastore and returns the output in single precision. Each column of the output is a separate signal from the datastore. The output may have fewer columns than the batch size if the datastore does not have enough records.
function batchout = helperReadBatch(ds,N,batchsize) % This function is only in support of Wavelet Toolbox examples. It may % change or be removed in a future release. % % batchout = readReadBatch(ds,N,batchsize) where ds is the Datastore and % ds is the Datastore % batchsize is the batchsize kk = 1; while(hasdata(ds)) && kk <= batchsize tmpRead = read(ds); batchout(:,kk) = cast(tmpRead(1:N),"single"); %#ok<AGROW> kk = kk+1; end end
Copyright 2021, The MathWorks, Inc.