生成的代码和 MATLAB 代码之间的差异
为了将 MATLAB® 代码转换为高效的 C/C++ 代码,代码生成器引入了优化,有意使生成的代码与原始源代码具有不同的行为,并且有时产生不同的结果。
以下是一些差异:
在以下情形中会出现这些差异:
使用
codegen命令或 MATLAB Coder™ 生成 MEX 和独立的 C/C++ 代码。通过使用
fiaccel(Fixed-Point Designer) 命令生成 MEX 来实现定点代码加速。使用 Simulink® 进行 MATLAB Function (Simulink) 模块仿真。
当您运行生成的 fiaccel MEX、C/C++ MEX 或独立的 C/C++ 代码时,运行时错误检查可以检测到其中的一些差异。默认情况下,对 MEX 代码启用运行时错误检查,对独立 C/C++ 代码禁用运行时错误检查。为帮助您在部署代码之前识别和解决差异,代码生成器将差异的一部分报告为潜在差异。
具有多种可能输出的函数
某些数学运算,如矩阵的奇异值分解和特征值分解,可以有多个答案。实现此类运算的两种不同算法可能会为相同的输入值返回不同的输出。相同算法的两种不同实现也可能会出现这种行为。
对于此类数学运算,使用生成代码中的对应函数与使用 MATLAB 可能会为相同的输入值返回不同的输出。要查看某个函数是否有这种行为,请在对应的函数参考页中,参阅扩展功能下的 C/C++ 代码生成部分。此类函数的示例包括 svd 和 eig。
在运行时传递输入参量名称
假设 foo 是使用名称-值参量验证的函数。当您从另一个函数 bar 调用 foo 时,代码生成器必须能够确定您在编译时提供给 foo 的名称。
如果在运行时传递参量名称,在大多数情况下代码生成都会失败。请参阅名称必须为编译时常量。
在某些情况下,代码生成器会将您传递的名称赋给可选的位置或重复输入参量。在这种情况下,虽然能成功生成代码,但会出现警告,生成的代码可能会产生与 MATLAB 执行不同的结果。以如下函数为例:
function out = myNamedArg_warns(a,b) out = local(a,b); end function out = local(varargin,args) arguments (Repeating) varargin end arguments args.x args.y end if isfield(args,'x') && isfield(args,'y') out = args.x / args.y; elseif isfield(args,'x') out = args.x; else out = varargin{1}; end end
MATLAB 执行的行为
如果使用 'x' 作为第一个输入参量调用 myNamedArg_warns,则 MATLAB 会将它与函数 local 的第一个名称-值参量进行匹配。
myNamedArg_warns('x',5)ans =
5相反,如果您调用 myNamedArg_warns 并将 'z' 作为第一个输入参量(与 local 的任一名称-值参量都不匹配),则 MATLAB 会将输入赋给 varargin 的元素。
myNamedArg_warns('z',5)
ans =
'z'生成的代码的行为
尝试通过运行 codegen 命令来生成 MEX。将第一个参量的类型指定为字符标量,将第二个参量的类型指定为双精度标量。代码生成成功,但出现警告。
codegen myNamedArg_warns -args {'x',2}
Warning:This argument is not constant, and therefore does not match against a name-value argument inside 'myNamedArg_warns/local' during code generation.Code generation might fail or produce results that do not agree with MATLAB if a name passed at a call site is not known during code generation.(警告:此参量不是常量,因此在代码生成过程中无法匹配 'myNamedArg_warns/local' 内部的名称-值参量。如果在代码生成期间不知道在调用点处传递的名称,代码生成可能会失败或生成与 MATLAB 不一致的结果。)
不管您是将 'x' 还是 'z' 作为第一个输入参量传递,生成的 MEX 都会将其赋给 varargin 的第一个元胞。
myNamedArg_warns_mex('x',5)ans =
'x'myNamedArg_warns_mex('z',5)ans =
'z'解决方法. 要使代码生成器能够将第一个输入与函数 local 的名称-值参量匹配,请将第一个输入声明为值为 'x' 的编译时常量。您可以通过将 coder.Constant 函数与 codegen 命令的 -args 选项结合使用来完成此操作。
codegen myNamedArg_warns -args {coder.Constant('x'),2}
Code generation successful.
现在,生成的 MEX 的行为与 MATLAB 行为一致,尽管 MEX 无法接受除 'x' 之外的任何值作为第一个输入。
myNamedArg_warns_mex('x',5)ans =
5
myNamedArg_warns_mex('z',5)Constant function parameter 'a' has a different run-time value than the compile-time value.(常量函数参数 'a' 的运行时值与编译时值不同。)
空的重复输入参量
在代码生成中,如果重复输入参量(在 arguments 块中声明)在运行时为空,则该参量的大小为 0x0。相反,在 MATLAB 执行中,空的重复输入参量的大小是 1x0。
以如下函数为例:
function out = testVararginSize out = local; end function out = local(varargin) arguments (Repeating) varargin end out = size(varargin); end
在 MATLAB 中运行 testVararginSize 会返回 [1 0]。如果您为 testVararginSize 生成 MEX 并运行生成的 MEX,您将得到 [0 0]。然而,通过使用 length(varargin) 或 numel(varargin) 来迭代 varargin 的元素会在 MATLAB 和代码生成中产生相同的行为。
有条件赋值的输出的输出参量验证
如果在代码生成过程中为某输出参量进行了类型赋值,则代码生成器会验证该输出参量。相反,如果在 MATLAB 函数返回时为输出参量赋值,则 MATLAB 执行会验证该输出参量。
在大多数情况下,这种潜在行为差异不会导致生成的代码的行为与 MATLAB 不同。下面的函数示例中体现了这种差异:
function outerFunc(in) innerFunc(in); end function out = innerFunc(inputVal) arguments (Output) out {mustBePositive} end if inputVal > 0 out = inputVal; end end
在 MATLAB 中,对于所有双精度输入,func 的执行都成功。如果输入为正值,则对 out 赋予此正值,并且验证器 mustBePositive 在没有断言的情况下运行。如果输入为负值或零,则不会对 out 赋值,也不会对其进行验证。
尝试为 func 生成代码。将输入类型指定为双精度标量。
codegen outerFunc -args 0
Variable 'out' is not fully defined on some execution paths.For code generation, all variables must be fully defined before use.(变量 'out' 在某些执行路径中未完全定义。要进行代码生成,所有变量在使用前都必须完全定义。)
由于变量 out 在一个执行路径中被赋予双精度标量值,代码生成在编译时会将双精度标量类型赋给 out。然后,代码生成器尝试对 out 执行验证,如果 if 条件失败,则认为它未完全定义。请参阅解决问题:变量在使用前必须完全定义。
写入 ans 变量
当您在未指定输出参量的情况下运行 MATLAB 代码并返回输出时,MATLAB 会将输出隐式写入 ans 变量中。如果工作区中已存在变量 ans,MATLAB 会将其值更新为返回的输出。
从此类 MATLAB 代码生成的代码不会将输出隐式写入 ans 变量。
例如,定义 MATLAB 函数 foo,它在第一行中显式创建 ans 变量。在第二行执行时,该函数会隐式更新 ans 的值。
function foo %#codegen ans = 1; 2; disp(ans); end
在命令行中运行 foo。ans 的最终值,即 2,显示在命令行上。
foo
2
从 foo 生成一个 MEX 函数。
codegen foo运行生成的 MEX 函数 foo_mex。此函数显式创建 ans 变量,并为其赋值 1。但是,foo_mex 并不将 ans 的值隐式更新为 2。
foo_mex
1
逻辑短路
假设您的 MATLAB 代码中逻辑运算符 & 和 | 放在方括号([ 和 ])内。对于这种代码模式,生成的代码不会对这些逻辑运算符采用短路行为,但某些 MATLAB 执行会采用短路行为。请参阅提示和提示。
例如,定义 MATLAB 函数 foo,该函数在 if...end 模块的条件表达式中使用方括号内的 & 运算符。
function foo if [returnsFalse() & hasSideEffects()] end end function out = returnsFalse out = false; end function out = hasSideEffects out = true; disp('This is my string'); end
& 运算符的第一个参量始终是 false,并确定条件表达式的值。因此,在 MATLAB 执行中,使用短路,并且不计算第二个参量。因此,foo 在执行期间不会调用 hasSideEffects 函数,也不会在命令行显示任何内容。
为 foo 生成一个 MEX 函数。调用生成的 MEX 函数 foo_mex。
foo_mex
This is my string
在生成的代码中,没有使用短路。因此,调用 hasSideEffects 函数,字符串显示在命令行中。
循环索引溢出
假设 for 循环结束值等于或接近循环索引数据类型的最大值或最小值。在生成的代码中,循环索引的最后一次递增或递减可能会导致索引变量溢出。索引溢出可能导致无限循环。
启用内存完整性检查时,如果代码生成器检测到循环索引可能溢出,它会报告错误。软件错误检查是保守型的。它可能会误报循环索引溢出。默认情况下,内存完整性检查对 MEX 代码启用,对独立 C/C++ 代码禁用。请参阅使用 MEX 函数检查 MATLAB 代码中的问题和Generate Standalone C/C++ Code That Detects and Reports Run-Time Errors。
为了避免循环索引溢出,请使用下表中的解决方法。
| 可能导致溢出的循环条件 | 解决方法 |
|---|---|
| 如果循环不必覆盖整数类型的全部范围,请重写循环,使结束值不等于整数类型的最大值。例如,将: N=intmax('int16')
for k=N-10:Nfor k=1:10 |
| 如果循环不必覆盖整数类型的全部范围,请重写循环,使结束值不等于整数类型的最小值。例如,将: N=intmin('int32')
for k=N+10:-1:Nfor k=10:-1:1 |
| 如果循环必须覆盖整数类型的全部范围,请将循环的开始值、步长值和结束值的类型转换为更大的整数或双精度值。例如,重写: M= intmin('int16');
N= intmax('int16');
for k=M:N
% Loop body
endM= intmin('int16');
N= intmax('int16');
for k=int32(M):int32(N)
% Loop body
end |
| 重写循环,使最后一次循环迭代中的循环索引等于结束值。 |
使用单精度操作数对 for 循环进行索引
假设在您的 MATLAB 代码中,您正在对具有冒号运算符的 for 循环进行索引,其中至少一个冒号操作数是 single 类型的操作数,并且迭代次数大于 flintmax('single') = 16777216。当所有这些条件都满足时,代码生成可能会产生运行时或编译时错误,因为生成代码为循环索引变量计算的值与 MATLAB 计算的值不同。
以如下 MATLAB 代码为例:
function j = singlePIndex n = flintmax('single') + 2; j = single(0); for i = single(1):single(n) j = i; end end
此代码片段会在 MATLAB 中执行,但它会导致编译时或运行时错误,因为循环索引变量 i 的值在生成代码中的计算方式不同。代码生成器显示编译时或运行时错误,并停止代码生成或执行以防止出现这种差异。
为了避免这种差异,请用双精度类型或整数类型操作数替换单精度类型操作数。
有关运行时错误的详细信息,请参阅Generate Standalone C/C++ Code That Detects and Reports Run-Time Errors。
未执行的 for 循环的索引
在您的 MATLAB 代码和生成代码中,在一个 for 循环执行完成后,索引变量的值等于其在 for 循环的最后一次迭代中的值。
在 MATLAB 中,如果循环不执行,则索引变量的值存储为 [ ](空矩阵)。在生成代码中,如果循环不执行,则索引变量的值不同于 MATLAB 索引变量。
如果在运行时提供
for循环的开始和结束变量,则索引变量的值等于范围的开始值。以如下 MATLAB 代码为例:function out = indexTest(a,b) for i = a:b end out = i; end
假设
a和b作为1和-1传递。则for循环不会执行。在 MATLAB 中,out被赋值为 [ ]。在生成代码中,out被赋予a的值,即1。如果在编译时间之前提供
for循环的开始和结束值,则在 MATLAB 和生成的代码中都会赋予索引变量值 [ ]。以如下 MATLAB 代码为例:function out = indexTest for i = 1:-1 end out = i; end
在 MATLAB 和生成的代码中,
out都被赋值为 [ ]。
字符大小
MATLAB 支持 16 位字符,但生成的代码以 8 位字符表示,这是适用于大多数嵌入式语言(如 C)的标准大小。请参阅代码生成中的字符编码。
表达式中的计算顺序
生成的代码不强制指定表达式中的计算顺序。对于大多数表达式,计算的顺序并不重要。对于具有副作用的表达式,生成的代码可能以不同于原始 MATLAB 代码的顺序产生副作用。产生副作用的表达式包括:
修改持久性或全局变量的表达式
将数据显示到屏幕的表达式
将数据写入文件的表达式
修改句柄类对象属性的表达式
此外,生成的代码不强制非短路逻辑运算符的计算顺序。
为获得更可预测的结果,最好在编码时根据计算顺序将表达式拆分为多个语句。
重写
A = f1() + f2();
为
A = f1(); A = A + f2();
使生成的代码在调用
f2之前调用f1。将多输出函数调用的输出赋给不相互依赖的变量。例如,重写
[y, y.f, y.g] = foo;
为
[y, a, b] = foo; y.f = a; y.g = b;
当您访问元胞数组的多个元胞的内容时,将结果赋给不相互依赖的变量。例如,重写
[y, y.f, y.g] = z{:};为
[y, a, b] = z{:}; y.f = a; y.g = b;
构造函数句柄时的名称解析
MATLAB 和代码生成遵循不同优先级规则来解析符号 @ 后面的名称。这些规则不适用于匿名函数。下表总结了这些优先级规则。
| 表达式 | MATLAB 中的优先顺序 | 代码生成中的优先顺序 |
|---|---|---|
不包含句点的表达式,例如 @x | 嵌套函数、局部函数、私有函数、路径函数 | 局部变量、嵌套函数、局部函数、私有函数、路径函数 |
仅包含一个句点的表达式,例如 @x.y | 局部变量、路径函数 | 局部变量、路径函数(与 MATLAB 相同) |
包含多个句点的表达式,例如 @x.y.z | 路径函数 | 局部变量、路径函数 |
如果 x 是局部变量且本身就是函数句柄,则生成代码和 MATLAB 对表达式 @x 的解释将有所不同:
MATLAB 生成错误。
生成代码将
@x解释为x本身的函数句柄。
以下示例说明对于包含两个句点的表达式在行为上的差异。
假设您的当前工作文件夹包含一个 MATLAB 命名空间 x,该命名空间包含另一个命名空间 y,其中又包含函数 z。当前工作文件夹还包含您要为其生成代码的入口函数 foo。
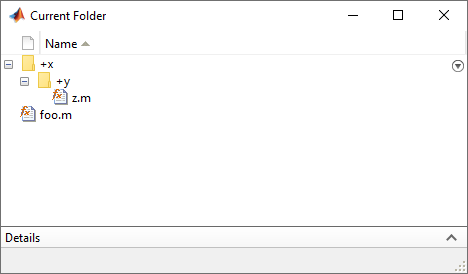
以下是文件 foo 的定义:
function out = foo x.y.z = @()'x.y.z is an anonymous function'; out = g(x); end function out = g(x) f = @x.y.z; out = f(); end
以下是函数 z 的定义:
function out = z out = 'x.y.z is a namespace function'; end
为 foo 生成一个 MEX 函数。分别调用生成的 MEX 函数 foo_mex 和 MATLAB 函数 foo。
codegen foo
foo_mex
fooans =
'x.y.z is an anonymous function'
ans =
'x.y.z is a namespace function'生成代码产生第一个输出。MATLAB 产生第二个输出。代码生成将 @x.y.z 解析为在 foo 中定义的局部变量 x。MATLAB 将 @x.y.z 解析为在 x.y 命名空间内的 z。
终止行为
生成的代码与 MATLAB 源代码的终止行为不一致。例如,如果无限循环不具有副作用,则优化会从生成的代码中删除它们。因此,即使对应的 MATLAB 代码不会终止,生成的代码也可能会终止。
可变大小 N 维数组的大小
对于可变大小 N 维数组,size 函数在生成的代码中返回的结果可能与在 MATLAB 源代码中不同。size 函数有时会在生成的代码中返回尾部维(单一维),但在 MATLAB 中始终会丢弃尾部维。例如,对于维度为 [4 2 1 1] 的 N 维数组 X,size(X) 可能会在生成的代码中返回 [4 2 1 1],但在 MATLAB 中始终返回 [4 2]。请参阅在确定可变大小 N 维数组的大小方面与 MATLAB 的不兼容性。
空数组的大小
空数组的大小在生成的代码中可能与 MATLAB 源代码中不同。请参阅在确定空数组的大小方面与 MATLAB 的不兼容性。
删除数组元素所生成的空数组的大小
删除数组的所有元素将生成空数组。此空数组的大小在生成的代码中可能与在 MATLAB 源代码中不同。
| 情形 | 示例代码 | MATLAB 中空数组的大小 | 生成的代码中空数组的大小 |
|---|---|---|---|
使用 colon 运算符 (:) 删除 m×n 数组的所有元素。 | coder.varsize('X',[4,4],[1,1]);
X = zeros(2);
X(:) = [];
| 0-by-0 | 1-by-0 |
使用 colon 运算符 (:) 删除行向量的所有元素。 | coder.varsize('X',[1,4],[0,1]);
X = zeros(1,4);
X(:) = []; | 0-by-0 | 1-by-0 |
使用 colon 运算符 (:) 删除列向量的所有元素。 | coder.varsize('X',[4,1],[1,0]);
X = zeros(4,1);
X(:) = []; | 0-by-0 | 0-by-1 |
| 通过一次删除一个元素来删除列向量的所有元素。 | coder.varsize('X',[4,1],[1,0]); X = zeros(4,1); for i = 1:4 X(1)= []; end | 1-by-0 | 0-by-1 |
增大在运行时初始化为标量的可变大小列元胞数组
在 MATLAB 执行中,如果您使用 {end+1} 索引来增大标量元胞数组,则元胞数组将沿第二个维度增大并生成一个行元胞数组。例如,定义函数 growCell:
function z = growCell(n, m) for i = 1:m n{end+1} = m; end z = n; end
使用示例输入调用 growCell:
growCell({2}, 3)ans =
1×4 cell array
{[2]} {[3]} {[3]} {[3]}相反,在代码生成中,假设:
您在编译时将元胞数组指定为可变大小的列类型(例如,
:Inf x 1),并且在运行时将此元胞数组初始化为标量。
在这种情况下,生成的代码沿第一个维度增大标量元胞数组,并生成一个列元胞数组。例如,为 growCell 生成 MEX 代码。将输入 n 指定为 :Inf x 1 元胞数组,以双精度作为基础类型。将输入 m 指定为双精度标量类型。
codegen growCell -args {coder.typeof({0}, [Inf 1], [1 0]), 1}
Code generation successful.
使用与之前相同的输入运行生成的 MEX。
growCell_mex({2}, 3)ans =
4×1 cell array
{[2]}
{[3]}
{[3]}
{[3]}单精度和双精度操作数的二元按元素运算
如果您的 MATLAB 代码包含涉及单精度类型操作数和双精度类型操作数的二元按元素运算,则生成代码的运算结果与 MATLAB 的运算结果可以会稍有不同。
对于此类运算,MATLAB 会先将两项操作数都转换为双精度类型,并用双精度类型执行运算。然后,MATLAB 再将运算结果转换为单精度类型并返回结果。
而生成代码则是将双精度类型操作数转换为单精度类型。然后用两个单精度类型执行运算并返回结果。
例如,定义一个 MATLAB 函数 foo,用它调用二元按元素运算 plus。
function out = foo(a,b) out = a + b; end
定义一个单精度类型的变量 s1 和一个双精度类型的变量 d1。为 foo 生成一个 MEX 函数,该函数接受单精度类型输入和双精度类型输入。
s1 = single(1.4e32); d1 = -5.305e+32; codegen foo -args {s1, d1}
使用 s1 和 d1 作为输入调用 foo 和 foo_mex。比较两个结果。
ml = foo(s1,d1); mlc = foo_mex(s1,d1); ml == mlc
ans = logical 0
比较的输出是逻辑值 0,这表明生成代码和 MATLAB 对这些输入分别产生了不同结果。
浮点数值结果
在下列情况下,生成的代码可能不会生成与 MATLAB 相同的浮点数值结果:
浮点 for 循环变量
代码生成器使用与 MATLAB 不同的算法计算循环迭代次数。当 for 循环具有浮点步长、起始值或结束值时,生成的代码计算的迭代次数可能与 MATLAB 计算的循环迭代次数不同。在这种情况下,生成的 MEX 函数在运行时会生成错误。请参阅Resolve Error: Cannot Determine the Exact Number of Iterations for a Loop。
NaN 和无穷
当 NaN 和 Inf 值在数学上没有意义时,它们在生成的代码中的模式可能不会与在 MATLAB 代码中完全相同。例如,如果 MATLAB 输出包含 NaN,生成的代码的输出也应包含 NaN,但不一定在相同的位置。
NaN 的位模式在 MATLAB 代码输出和生成的代码输出之间可能有所不同,这是因为用于生成代码的 C99 语言标准未对所有实现中的 NaN 指定唯一位模式。请避免比较不同实现中的位模式,例如,在 MATLAB 输出和 SIL 或 PIL 输出之间进行比较。
负零
在浮点类型中,值 0 具有正号或负号。在算术上,0 等于 -0,但某些运算对 0 输入符号敏感。示例包括 rdivide、atan2、atan2d 和 angle。除以 0 会生成 Inf,而除以 -0 会生成 -Inf。同样,atan2d(0,-1) 生成 180,而 atan2d (-0,-1) 生成 -180。
如果代码生成器检测到某浮点变量只接受适当范围的整数值,则代码生成器可以在生成的代码中对该变量使用整数类型。如果代码生成器对该变量使用整数类型,则该变量将 -0 存储为 +0,因为整数类型不存储值 0 的符号。如果生成的代码将该变量强制转换回浮点类型,则 0 的符号为正。除以 0 会生成 Inf,而不是 -Inf。同样,atan2d(0,-1) 生成 180,而不是 -180。
在其他情况下,生成的代码可能会以不同于 MATLAB 的方式处理 -0。例如,假设您的 MATLAB 代码使用 z = min(x,y) 计算两个双精度标量值 x 和 y 的最小值。生成的 C 代码中对应的行可能是 z = fmin(x,y)。函数 fmin 是在 C 编译器的运行时数学库中定义的。由于比较运算 0.0 == -0.0 在 C/C++ 中返回 true,因此编译器对 fmin 的实现可能会为 fmin(0.0,-0.0) 返回 0.0 或 -0.0。
将双精度值转换为枚举成员
对于类型为 double 的非整数运行时值 x,生成的代码计算 MyEnum(x) 的方式与 MATLAB 执行不同。此处,MyEnum 是从整数类型派生的 MATLAB 枚举类。在计算 MyEnum(x) 时:
执行内存完整性检查的生成的 MEX 函数会生成运行时错误
不执行内存完整性检查的生成的 MEX 函数或生成的独立代码会生成
MyEnum(floor(x))MATLAB 执行会生成
MyEnum(round(x))
检查内存完整性配置参数控制生成的 MEX 函数是否执行内存完整性检查。默认情况下启用此参数。
以此入口函数为例:
function u = xMyEnum(x) arguments x (1,1) double end u = MyEnum(x); end
此处枚举 MyEnum 定义为:
classdef MyEnum < int32 enumeration ONE(1), TWO(2) end end
如果您使用默认配置设置生成 MEX 函数,然后使用非整数输入运行 MEX 函数,则会得到错误。例如,
codegen xMyEnumCode generation successful.
xMyEnum_mex(1.5)
Expected a value representable in the C type 'int'. Found 1.500000 instead. Error in xMyEnum2 (line 5)
相反,如果您在禁用检查内存完整性参数的状态下生成 MEX 函数,则生成的代码会将 MyEnum(x) 计算为 MyEnum(floor(x))。
cfg = coder.config("mex"); cfg.IntegrityChecks = false; codegen -config cfg xMyEnum
Code generation successful.
xMyEnum_mex(1.3)
ans =
MyEnum enumeration
ONExMyEnum_mex(1.7)
ans =
MyEnum enumeration
ONE然而,MATLAB 执行将 MyEnum(x) 计算为 MyEnum(round(x))。
xMyEnum(1.3)
ans =
MyEnum enumeration
ONExMyEnum(1.7)
ans =
MyEnum enumeration
TWO代码生成目标
coder.target 函数在 MATLAB 中返回的值与在生成的代码中返回的值不同。这是为了帮助您确定您的函数是在 MATLAB 中执行,还是已针对仿真或代码生成目标进行编译。请参阅 coder.target。
MATLAB 类属性初始化
在代码生成之前,MATLAB 在类加载时计算类默认值。代码生成器使用 MATLAB 计算的值。它不会重新计算默认值。如果属性定义使用函数调用来计算初始值,则代码生成器不会执行此函数。如果函数具有修改全局变量或持久变量等副作用,则生成的代码可能会产生与 MATLAB 不同的结果。有关详细信息,请参阅为代码生成定义类属性。
在 resetImpl 方法中读取具有默认值的 System object 属性
以 System object™ 定义为例,其中您为一个属性赋予默认值,但没有在构造函数中显式赋予此值。您还可以在 resetImpl 方法中读取此属性。例如:
classdef A < matlab.System properties property = 1; end methods (Access = 'protected') function result = stepImpl(~, arg) result = arg; end function resetImpl(this) disp(this.property); end end end
如果您的 MATLAB 代码满足以下附加条件,则在生成的代码和 MATLAB 执行之间读取此属性的结果可能会有所不同:
在
resetImpl方法之外无法读取此属性对
reset方法的调用并不始终先于对此属性的写入操作您的 MATLAB 代码不包含对
step、setupAndReset或resetImpl方法的直接调用
要了解行为差异,请定义以下使用 System object A 的 MATLAB 入口函数:
function main x = A; setup(x); reset(x); end
如果在 MATLAB 中执行 main,该函数将显示值 1。但是,如果为 main 生成 MEX 函数并执行 main_mex,该函数可能会显示任何值。通常,它会显示 0。
要生成行为与 MATLAB 一致的代码,请在 System object 的构造函数中显式赋予属性初始值。例如,对于 System object A,通过添加此构造函数来修改定义:
classdef A < matlab.System ... methods function this = A this.property = 1; end end ... end
具有 set 方法的嵌套属性赋值中的 MATLAB 类
当您为句柄对象属性赋值时,如果该属性本身就是另一个对象的属性(依此类推),则生成的代码可以调用 MATLAB 不调用的句柄类 set 方法。
例如,假设您定义一组变量,使得 x 是句柄对象,pa 是对象,pb 是句柄对象,pc 是 pb 的属性。然后进行嵌套属性赋值,例如:
x.pa.pb.pc = 0;
在本例中,生成的代码调用对象 pb 的 set 方法和 x 的 set 方法。MATLAB 仅调用 pb 的 set 方法。
具有未分配属性的别名嵌套句柄对象
如果您的 MATLAB 对象有一个属性只是偶尔被赋值(也就是说,某个计算路径会对该属性赋值,而另一个路径则不会)但始终使用,代码生成通常会失败。相反,在 MATLAB 中,代码执行时没有错误,任何未赋值的属性都自动初始化为空矩阵。
但是,如果满足所有以下条件,代码生成的行为会有所不同:
源 MATLAB 代码包含句柄对象,其属性是另一个句柄对象。
有一个函数通过多个输入接收同一句柄对象。也就是说,所有这些输入都以别名形式指向同一对象。
内部句柄对象有一个仅在某些计算路径中被赋值的属性。在其他路径中,MATLAB 自动将该属性初始化为空矩阵。这种条件赋值发生在上面第二个条件中所述的函数内部。
对于这样的 MATLAB 代码模式,代码生成可能会成功,而不是生成错误。在生成的 C/C++ 代码中,此有条件定义的属性有未定义的值(在没有显式定义它的路径中),而不等于空矩阵。
例如,定义句柄类 H:
classdef H < handle properties p end end
定义入口函数 main:
function out = main a = H(); a.p = H(); a.p.p = 1; out = foo(a, a); end
函数 main 调用接收两个输入的函数 foo,这两个输入均为 H 的同一实例。
function out = foo(x, y) x.p = H; % x.p.p is now unset. Because x=y, y.p.p is unset. out = y.p.p; % Generated code does not error. It assigns the undefined value of y.p.p to out. end
在 MATLAB 中,函数 main 返回 []。相反,如果您生成 MEX 函数 main_mex 并运行它,该函数将返回随机值。
MATLAB 句柄类析构函数
在下列情况下,生成的代码中句柄类析构函数的行为可能与 MATLAB 中的行为不同:
有些独立对象在 MATLAB 中的销毁顺序可能与生成的代码中的顺序不同。
生成的代码中的对象的生命周期可能与它们在 MATLAB 中的生命周期不同。
生成的代码不销毁部分构造的对象。如果句柄对象在运行时未完全构造,则生成的代码将生成错误消息,但不为该对象调用
delete方法。对于 System object,如果在setupImpl中存在运行时错误,则生成的代码不为该对象调用releaseImpl。MATLAB 确实会调用
delete方法来销毁部分构造的对象。
有关详细信息,请参阅句柄类析构函数的代码生成。
可变大小数据
复数
请参阅复数数据的代码生成。
将使用连续一元运算符的字符串转换为 double
如果将包含多个连续一元运算符的字符串转换为 double,则在 MATLAB 和生成的代码之间可能产生不同结果。以如下函数为例:
function out = foo(op) out = double(op + 1); end
对于输入值 "--",该函数将字符串 "--1" 转换为 double。在 MATLAB 中,结果为 NaN。在生成的代码中,结果为 1。
显示函数
MATLAB 代码中省略分号的语句和表达式隐式调用 display 函数。您也可以显式调用 display,如下所示:
display(2+3);
5
为调用 display 函数的 MATLAB 代码生成的 MEX 代码将保留对此函数的调用并显示输出。在为无权访问 MATLAB Runtime 的目标生成的独立代码中,删除了对 display 的隐式和显式调用。这包括对 display 的覆盖类方法的调用。
要在为其他目标生成的代码中显示文本,请在 MATLAB 类中覆盖 disp 函数。例如:
%MATLAB Class classdef foo methods function obj = foo end function disp(self) disp("Overridden disp"); end end end %Entry-point Function function callDisp a = foo; disp(a); end
为入口函数生成的代码如下所示:
/* Include Files */
#include "callDisp.h"
#include <stdio.h>
/* Function Definitions */
/*
* Arguments : void
* Return Type : void
*/
void callDisp(void)
{
printf("%s\n", "Overridden disp");
fflush(stdout);
}
函数句柄差异
通过 MATLAB 中的函数句柄调用 display 也会输出变量的名称。例如,在 MATLAB 中运行此函数会产生以下输出:
function displayDiff z = 10; f = @display; f(z) end
z =
10但是,为此代码片段生成的代码只输出值 10。
