stepinfo

上升时间、稳定时间和其他阶跃响应特征

全页折叠

语法

S = stepinfo(sys)

S = stepinfo(y,t)

S = stepinfo(y,t,yfinal)

S = stepinfo(y,t,yfinal,yinit)

S = stepinfo(___,'SettlingTimeThreshold',ST)

S = stepinfo(___,'RiseTimeLimits',RT)

说明

stepinfo 可用于计算动态系统模型或阶跃响应数据数组的阶跃响应特征。对于阶跃响应 y(t)，stepinfo 计算相对于 y_init 和 y_final 的特征，其中 y_init 是初始偏移量（即施加阶跃之前的值），y_final 是响应的稳态值。这些值取决于您使用的语法。

对于动态系统模型 sys，stepinfo 使用 y_init = 0 且 y_final = 稳态值。
对于阶跃响应数据数组 [y,t]，stepinfo 使用 y_init = 0 且 y_final = y 的最后一个采样值，除非您显式指定这些值。

有关 stepinfo 如何计算阶跃响应特征的详细信息，请参阅算法。

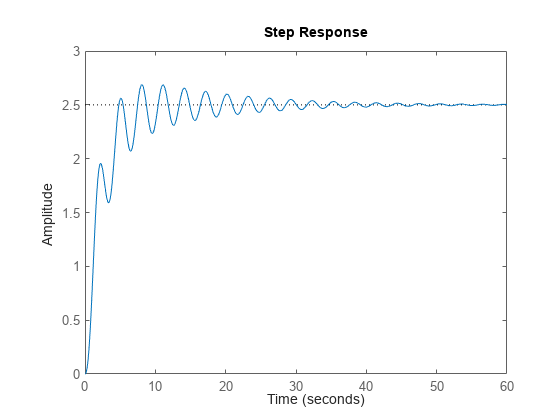
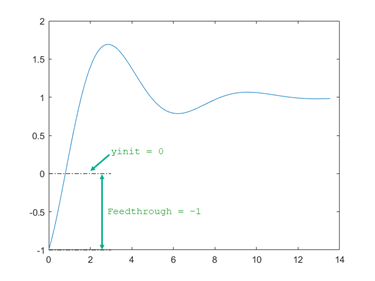
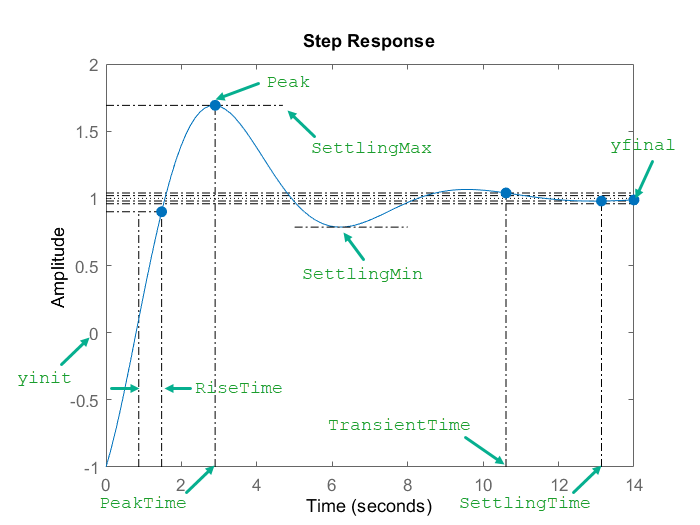
下图说明了 stepinfo 为阶跃响应计算的一些特征。对于此响应，假设当 t < 0 时，y(t) = 0，因此 y_init = 0。

Step response characteristics. The figure shows peak response, peak time, rise time, settling time, and transient time of the response.

S = stepinfo(sys) 计算动态系统模型 sys 的阶跃响应特征。此语法使用 y_init = 0 且 y_final = 稳态值来计算依赖于这些值的特征。

示例

S = stepinfo(y,t) 根据阶跃响应数据数组 y 和相应的时间向量 t 计算阶跃响应特征。对于 SISO 系统响应，y 是一个向量，其条目数与 t 相同。对于 MIMO 响应数据，y 是一个包含每个 I/O 通道响应的数组。此语法使用 y_init = 0，并将 y 中的最后一个值（或每个通道相应响应数据中的最后一个值）作为 y_final。

S = stepinfo(y,t,yfinal) 计算相对于稳态值 yfinal 的阶跃响应特征。当您知道预期的系统稳态响应由于测量噪声等原因而与 y 中的最后一个值不同时，此语法非常有用。此语法使用 y_init = 0。

对于 SISO 响应，t 和 y 是具有相同长度 NS 的向量。对于具有 NU 个输入和 NY 个输出的系统，您可以将 y 指定为 NS×NY×NU 数组（参见 step），并将 yfinal 指定为 NY×NU 数组。然后，stepinfo 返回一个 NY×NU 结构体数组 S，其中每个结构体包含对应每个 I/O 对组的响应特征。

示例

S = stepinfo(y,t,yfinal,yinit) 计算相对于响应初始值 yinit 的阶跃响应特征。当您的 y 数据具有初始偏移量（即阶跃发生之前 y 不为零）时，此语法非常有用。

对于 SISO 响应，t 和 y 是具有相同长度 NS 的向量。对于具有 NU 个输入和 NY 个输出的系统，您可以将 y 指定为 NS×NY×NU 数组，并将 yinit 指定为 NY×NU 数组。然后，stepinfo 返回一个 NY×NU 结构体数组 S，其中每个结构体包含对应每个 I/O 对组的响应特征。

示例

S = stepinfo(___,'SettlingTimeThreshold',ST) 允许您指定用于定义稳定时间和瞬态时间的阈值 ST。默认值为 ST = 0.02 (2%)。此语法可与上述任一输入参量组合结合使用。

示例

S = stepinfo(___,'RiseTimeLimits',RT) 允许您指定用于定义上升时间的下阈值和上阈值。默认情况下，上升时间是响应从初始值到稳态值变化区间的 10% 升到 90% 所需的时间 (RT = [0.1 0.9])。上阈值 RT(2) 也用于计算 SettlingMin 和 SettlingMax。这些值是响应达到上阈值后发生的响应的最小值和最大值。此语法可与上述任一输入参量组合结合使用。

示例

全部折叠

动态系统的阶跃响应特征

打开实时脚本

计算动态系统模型的阶跃响应特征，例如上升时间、稳定时间和超调。对于此示例，请使用连续时间传递函数：

$s y s = \frac{s^{2} + 5 s + 5}{s^{4} + 1.65 s^{3} + 5 s^{2} + 6.5 s + 2}$ .

创建传递函数并检查其阶跃响应。

sys = tf([1 5 5],[1 1.65 5 6.5 2]);
step(sys)

MATLAB figure

该图显示响应在几秒钟内上升，然后逐渐衰减到约为 2.5 的稳态值。使用 stepinfo 计算此响应的特征。

S = stepinfo(sys)

S = struct with fields:
         RiseTime: 3.8456
    TransientTime: 27.9762
     SettlingTime: 27.9762
      SettlingMin: 2.0689
      SettlingMax: 2.6873
        Overshoot: 7.4915
       Undershoot: 0
             Peak: 2.6873
         PeakTime: 8.0530

其中，该函数使用 $y_{init}$ = 0 来计算动态系统模型 sys 的特征。

默认情况下，稳定时间是误差保持在 $| y_{init} - y_{final} |$ 的 2% 以下所需的时间。结果 S.SettlingTime 显示，对于 sys，此情况发生在约 28 秒之后。上升时间的默认定义是响应从 $y_{init}$ = 0 到 $y_{final}$ 变化区间的 10% 升到 90% 所需的时间。S.RiseTime 显示，对于 sys，此上升发生在不到 4 秒的时间内。最大超调在 S.Overshoot 中返回。对于该系统，峰值 S.Peak 的出现时间为 S.PeakTime，其超调量约为稳态值的 7.5%。

MIMO 系统的阶跃响应特征

打开实时脚本

对于 MIMO 系统，stepinfo 返回一个结构体数组，其中每个条目包含系统相应 I/O 通道的响应特征。对于此示例，请使用一个双输出、双输入的离散时间系统。计算阶跃响应特征。

A = [0.68 -0.34; 0.34 0.68];
B = [0.18 -0.05; 0.04 0.11];
C = [0 -1.53; -1.12 -1.10];
D = [0 0; 0.06 -0.37];
sys = ss(A,B,C,D,0.2);

S = stepinfo(sys)

S=2×2 struct array with fields:
    RiseTime
    TransientTime
    SettlingTime
    SettlingMin
    SettlingMax
    Overshoot
    Undershoot
    Peak
    PeakTime

通过对 S 进行索引来访问特定 I/O 通道的响应特征。例如，检查 sys 的第一个输入到第二个输出的响应特征，对应于 S(2,1)。

S(2,1)

ans = struct with fields:
         RiseTime: 0.4000
    TransientTime: 2.8000
     SettlingTime: 3
      SettlingMin: -0.6724
      SettlingMax: -0.5188
        Overshoot: 24.6476
       Undershoot: 11.1224
             Peak: 0.6724
         PeakTime: 1

要访问特定值，请使用圆点表示法。例如，提取 (2,1) 通道的上升时间。

rt21 = S(2,1).RiseTime

rt21 = 
0.4000

指定稳定时间或上升时间的百分比

打开实时脚本

您可以使用 SettlingTimeThreshold 和 RiseTimeThreshold 分别更改稳定时间和上升时间的默认百分比，如算法部分所述。对于此示例，请使用以下系统：

$sys = \frac{s^{2} + 5 s + 5}{s^{4} + 1.65 s^{3} + 6.5 s + 2}$ .

创建传递函数。

sys = tf([1 5 5],[1 1.65 5 6.5 2]);

计算 sys 的响应误差保持在差距 $| y_{final} - y_{init} |$ 的 0.5% 以下所需的时间。为此，请将 SettlingTimeThreshold 设置为 0.5%（即 0.005）。

S1 = stepinfo(sys,SettlingTimeThreshold=0.005);
st1 = S1.SettlingTime

st1 = 
46.1325

计算 sys 的响应从 $y_{init}$ 到 $y_{final}$ 变化区间的 5% 升到 95% 所需的时间。为此，请将 RiseTimeThreshold 设置为包含这些边界的向量。

S2 = stepinfo(sys,RiseTimeThreshold=[0.05 0.95]);
rt2 = S2.RiseTime

rt2 = 
4.1690

您可以在同一计算中同时定义稳定时间和上升时间的百分比。

S3 = stepinfo(sys,...
    SettlingTimeThreshold=0.005, ...
    RiseTimeThreshold=[0.05 0.95])

S3 = struct with fields:
         RiseTime: 4.1690
    TransientTime: 46.1325
     SettlingTime: 46.1325
      SettlingMin: 2.0689
      SettlingMax: 2.6873
        Overshoot: 7.4915
       Undershoot: 0
             Peak: 2.6873
         PeakTime: 8.0530

从响应数据中提取阶跃响应特征

打开实时脚本

即使没有系统模型，您也可以从阶跃响应数据中提取阶跃响应特征。例如，假设您已经测量了您的系统对阶跃输入的响应，并将得到的响应数据保存在一个响应值向量 y 中，与这些响应值对应的时间存储在另一个向量 t 中。加载响应数据并对其进行检查。

load StepInfoData t y
plot(t,y)

Figure contains an axes object. The axes object contains an object of type line.

使用 stepinfo 根据此响应数据计算阶跃响应特征。如果您未指定稳态响应值 yfinal，则 stepinfo 会假定响应向量 y 中的最后一个值是稳态响应。由于数据中存在一些噪声，y 中的最后一个值可能不是真正的稳态响应值。当您知道稳态值应该是多少时，可以将其提供给 stepinfo。对于此示例，假设稳态响应为 2.4。

S1 = stepinfo(y,t,2.4)

S1 = struct with fields:
         RiseTime: 1.2897
    TransientTime: 19.6478
     SettlingTime: 19.6439
      SettlingMin: 2.0219
      SettlingMax: 3.3302
        Overshoot: 38.7575
       Undershoot: 0
             Peak: 3.3302
         PeakTime: 3.4000

由于数据中存在噪声，默认的稳定时间定义过于严格，导致得到近乎 20 秒的任意值。为了考虑噪声的影响，请将稳定时间阈值从默认的 2% 提高到 5%。

S2 = stepinfo(y,t,2.4,'SettlingTimeThreshold',0.05)

S2 = struct with fields:
         RiseTime: 1.2897
    TransientTime: 10.4201
     SettlingTime: 10.4149
      SettlingMin: 2.0219
      SettlingMax: 3.3302
        Overshoot: 38.7575
       Undershoot: 0
             Peak: 3.3302
         PeakTime: 3.4000

阶跃响应中瞬态时间与稳定时间的区别

打开实时脚本

当峰值误差 $e_{\max}$ 等于差距 $| y_{final} - y_{init} |$ （参见算法）时，稳定时间和瞬态时间是相等的。这种情况适用于无欠调或馈通且超调小于 100% 的模型。对于具有馈通、零点位于原点、具有不稳定零点（欠调）或大超调的模型，稳定时间和瞬态时间往往存在区别。

假设有以下模型。

sys1 - 具有直接馈通的系统
sys2 - 零点位于原点的系统
sys3 - 具有欠调的非最小相位系统
sys4 - 具有大超调的系统

s = tf("s");
sys1 = 1+tf(1,[1 1]);
sys2 = tf([1 0],[1 1]);
sys3 = tf([-3 1],[1 2 1]);
sys4 = (s/0.5 + 1)/(s^2 + 0.2*s + 1);

step(sys1,sys2,sys3,sys4)
grid on
legend("Feedthrough", ...
    "Zero at origin", ...
    "Nonminimum phase with undershoot", ...
    "Large overshoot")

MATLAB figure

计算阶跃响应特征。

S1 = stepinfo(sys1)

S1 = struct with fields:
         RiseTime: 1.6095
    TransientTime: 3.9121
     SettlingTime: 3.2190
      SettlingMin: 1.8005
      SettlingMax: 1.9993
        Overshoot: 0
       Undershoot: 0
             Peak: 1.9993
         PeakTime: 7.3222

S2 = stepinfo(sys2)

S2 = struct with fields:
         RiseTime: 0
    TransientTime: 3.9121
     SettlingTime: NaN
      SettlingMin: 6.6069e-04
      SettlingMax: 1
        Overshoot: Inf
       Undershoot: Inf
             Peak: 1
         PeakTime: 0

S3 = stepinfo(sys3)

S3 = struct with fields:
         RiseTime: 2.9198
    TransientTime: 6.5840
     SettlingTime: 7.3229
      SettlingMin: 0.9008
      SettlingMax: 1.0000
        Overshoot: 0
       Undershoot: 88.9301
             Peak: 1.0000
         PeakTime: 14.6905

S4 = stepinfo(sys4)

S4 = struct with fields:
         RiseTime: 0.3896
    TransientTime: 40.3317
     SettlingTime: 46.5052
      SettlingMin: -0.2796
      SettlingMax: 2.7571
        Overshoot: 175.7137
       Undershoot: 27.9629
             Peak: 2.7571
         PeakTime: 1.8850

检查绘图和特征。对于这些模型，稳定时间和瞬态时间不同，因为峰值误差超过了初始值和最终值之间的差距。对于诸如 sys2 之类的模型，由于稳态值为零，稳定时间返回为 NaN。

具有初始偏移量的数据的阶跃响应特征

打开实时脚本

在此示例中，您将根据具有初始偏移量的阶跃响应数据计算阶跃响应特征。这意味着在阶跃发生之前，响应数据的值不为零。

加载阶跃响应数据并检查绘图。

load stepDataOffset.mat
plot(stepOffset.Time,stepOffset.Data)

Figure contains an axes object. The axes object contains an object of type line.

如果您未指定 yfinal 和 yinit，则 stepinfo 会假定 yfinal 是响应向量 y 中的最后一个值，而 yinit 为零。当您知道稳态值和初始值是多少时，可以将它们提供给 stepinfo。其中，响应 yfinal 的稳态值为 0.9，初始偏移量 yinit 为 0.2。

根据此响应数据计算阶跃响应特征。

S = stepinfo(stepOffset.Data,stepOffset.Time,0.9,0.2)

S = struct with fields:
         RiseTime: 0.0084
    TransientTime: 1.0662
     SettlingTime: 1.0662
      SettlingMin: 0.8461
      SettlingMax: 1.0878
        Overshoot: 26.8259
       Undershoot: 0.0429
             Peak: 0.8878
         PeakTime: 1.0225

其中，该响应的峰值为 0.8878，因为 stepinfo 测量的是与 yinit 的最大偏差。

输入参数

全部折叠

`sys` — 动态系统
动态系统模型

动态系统，指定为 SISO 或 MIMO 动态系统模型。您可以使用的动态系统包括：

连续时间或离散时间数值 LTI 模型，如 tf、zpk 或 ss 模型。
广义或不确定的 LTI 模型，如 genss 或 uss (Robust Control Toolbox) 模型。（使用不确定模型需要 Robust Control Toolbox™ 软件。）对于广义模型，stepinfo 使用可调模块的当前值和不确定模块的标称值来计算阶跃响应特征。
辨识的 LTI 模型，如 idtf (System Identification Toolbox)、idss (System Identification Toolbox) 或 idproc (System Identification Toolbox) 模型。（使用辨识模型需要 System Identification Toolbox™ 软件。）

`y` — 阶跃响应数据
向量 | 数组

阶跃响应数据，指定为以下项之一：

对于 SISO 响应数据，为长度为 Ns 的向量，其中 Ns 是响应数据中的采样数
对于 MIMO 响应数据，为 Ns×Ny×Nu 的数组，其中 Ny 是系统输出的数量，Nu 是系统输入的数量

您可以使用 y 指定复数响应数据。 (自 R2025a 起)

`t` — 时间向量
向量

与 y 中的响应数据对应的时间向量，指定为长度为 Ns 的向量。

`yfinal` — 稳态值
标量 | 数组

稳态值，指定为标量或数组。

对于 SISO 响应数据，请指定一个标量值。
对于 MIMO 响应数据，请指定一个 Ny×Nu 的数组，其中每个条目提供相应系统通道的稳态响应值。

您可以使用 yfinal 指定复数最终值。 (自 R2025a 起)

如果您未提供 yfinal，则 stepinfo 会将 y 相应通道中的最后一个值用作稳态响应值。

仅当您提供阶跃响应数据作为输入时，才支持此参量。对于动态系统模型 sys 作为输入，stepinfo 使用 y_final = 稳态值来计算依赖于该值的特征。

`yinit` — 初始值
标量 | 数组

阶跃发生之前 y 的值，指定为标量或数组。

对于 SISO 响应数据，请指定一个标量值。
对于 MIMO 响应数据，请指定一个 Ny×Nu 的数组，其中每个条目提供相应系统通道的响应初始值。

您可以使用 yinit 指定复数初始值。 (自 R2025a 起)

如果您未提供 yinit，则 stepinfo 将使用零作为响应初始值。

对于无馈通的系统，t = 0 时的响应 y(0) 等于 y_init。但是，在存在馈通的情况下，由于 t = 0 处的不连续性，这两个量不同。

例如，下图显示了具有馈通的系统 sys = tf([-1 0.2 1],[1 0.7 1]) 的阶跃响应。

Step response of a system with feedthrough equal to negative1

其中，y_init 为零，馈通值为 -1。

仅当您提供阶跃响应数据作为输入时，才支持此参量。如果使用动态系统模型 sys 作为输入，stepinfo 将使用 y_init = 0 来计算依赖于该值的特征。

`ST` — 稳定时间阈值
0.02 (默认) | 0 到 1 之间的标量

用于定义稳定时间和瞬态时间的阈值，指定为 0 到 1 之间的标量值。要更改默认的稳定时间和瞬态时间定义（参见算法），请将 ST 设置为其他值。例如，要测量误差何时低于 5%，请将 ST 设置为 0.05。

`RT` — 上升时间阈值
`[0.1 0.9]` (默认) | 2 元素行向量

用于定义上升时间的阈值，指定为一个 2 元素行向量，元素为 0 到 1 之间的非降序值。要更改默认的上升时间定义（参见算法），请将 RT 设置为其他值。例如，要将上升时间定义为响应从初始值到稳态值期间从 5% 上升到 95% 所需的时间，请将 RT 设置为 [0.05 0.95]。

输出参量

全部折叠

`S` — 阶跃响应特征
结构体

阶跃响应特征，以包含以下字段的结构体形式返回：

RiseTime
TransientTime
SettlingTime
SettlingMin
SettlingMax
Overshoot
Undershoot
Peak
PeakTime

有关 stepinfo 如何定义这些特征的详细信息，请参阅算法。

对于 MIMO 模型或响应数据，S 是一个结构体数组，其中每个条目包含相应 I/O 通道的阶跃响应特征。例如，如果您提供一个 3 输入 3 输出的模型或一个响应数据数组，则 S(2,3) 包含从第三个输入到第二个输出的响应特征。有关示例，请参阅MIMO 系统的阶跃响应特征。

如果 sys 不稳定，则所有阶跃响应特征均为 NaN，但 Peak 和 PeakTime 除外，它们为 Inf。

算法

对于阶跃响应 y(t)，stepinfo 计算相对于 y_init 和 y_final 的特征。默认情况下，对于动态系统模型 sys，stepinfo 使用 y_init = 0 且 y_final = 稳态值。

下表显示了 stepinfo 如何计算每个特征。

阶跃响应特征	描述
`RiseTime`	响应从 y_init 到 y_final 变化区间的 10% 升到 90% 所需的时间
`TransientTime`	当 t ≥ T 时，第一个使得误差 \|y(t) – y_final\| ≤ SettlingTimeThreshold × e_max 的时间 T，其中 e_max 是 t ≥ 0 时的最大误差 \|y(t) – y_final\|。默认情况下，SettlingTimeThreshold = 0.02（峰值误差的 2%）。瞬态时间衡量瞬态动态特性消失的速度。
`SettlingTime`	当 t ≥ T 时，第一个使得误差 \|y(t) – y_final\| ≤ SettlingTimeThreshold × \|y_final – y_init\| 的时间 T。默认情况下，`SettlingTime` 衡量误差保持在 \|y_final – y_init\| 的 2% 以下所需的时间。
`SettlingMin`	响应上升后 y(t) 的最小值
`SettlingMax`	响应上升后 y(t) 的最大值
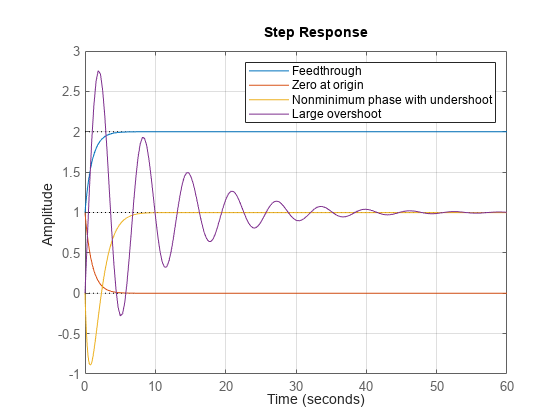
`Overshoot`	超调百分比。相对于归一化响应 y_norm(t) = (y(t) – y_init)/(y_final – y_init)，超调为零和 100 × max(y_norm(t) – 1) 中的较大者。
`Undershoot`	欠调百分比。相对于归一化响应 y_norm(t)，欠调为零和 –100 × min(y_norm(t) ) 中的较小者。
`Peak`	\|y(t) – y_init\| 的峰值
`PeakTime`	峰值出现的时间

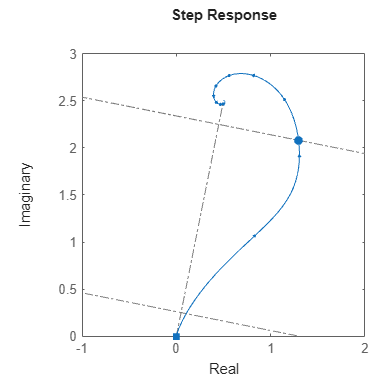
对于复数响应，stepinfo 通过将 y(t) 投影到从 y_init 到 y_final 所连成的射线上计算 RiseTime、Overshoot 和 Undershoot。复数响应的所有其他特征与上表中的定义相同，并基于 y、y_init 和 y_final 中复数值的模进行计算。下图显示了投影到从 y_init 到 y_final 的射线上的 10% 和 90% 上升时间点。 (自 R2025a 起)

Step response on a complex plane showing a ray from the initial point at the origin to the final point. The 90% rise-time point is marked on the response and this point is projected onto the ray.

版本历史记录

在 R2006a 中推出

全部展开

R2025a: 计算具有复系数的 LTI 系统的响应特征

您可以通过指定以下项之一来获得具有复数响应的 LTI 系统的阶跃响应特征：

具有复系数的动态系统模型
参量 y、yfinal 和 yinit 的复数值

R2021b: 响应特征计算变化

某些响应特征的计算方法已发生改变。此外，稳定时间的计算现在基于响应保持在初始值和最终值之间差距的指定阈值以下的速度。

下表总结了 stepinfo 返回的结构体字段的变化。

在 R2021b 之前 R2021b

在 R2021b 之前	R2021b
`RiseTime` - 响应从 y(1) 到 y_final 变化区间的 10% 升到 90% 所需的时间。	`RiseTime` - 响应从 y_init 到 y_final 变化区间的 10% 上升到 90% 所需的时间。
`SettlingTime` - 当 t ≥ T 时，第一个使得误差 \|y(t) – y_final\| ≤ SettlingTimeThreshold × e_max 的时间 T，其中 e_max 是 t ≥ 0 时的最大误差 \|y(t) – y_final\|。默认情况下，SettlingTimeThreshold = 0.02（峰值误差的 2%）。`SettlingTime` 衡量误差降至误差峰值的 2% 以下的时间。	`SettlingTime` - 当 t ≥ T 时，第一个使得误差 \|y(t) – y_final\| ≤ SettlingTimeThreshold × \|y_final – y_init\| 的时间 T。默认情况下，`SettlingTime` 衡量误差保持在 \|y_final – y_init\| 的 2% 以下所需的时间。
`Peak` - y(t) 的峰值绝对值。	`Peak` -y(t) – y_init 的峰值绝对值。

RiseTime - 响应从 y(1) 到 y_final 变化区间的 10% 升到 90% 所需的时间。

RiseTime - 响应从 y_init 到 y_final 变化区间的 10% 上升到 90% 所需的时间。

SettlingTime - 当 t ≥ T 时，第一个使得误差 |y(t) – y_final| ≤ SettlingTimeThreshold × e_max 的时间 T，其中 e_max 是 t ≥ 0 时的最大误差 |y(t) – y_final|。

默认情况下，SettlingTimeThreshold = 0.02（峰值误差的 2%）。SettlingTime 衡量误差降至误差峰值的 2% 以下的时间。

SettlingTime - 当 t ≥ T 时，第一个使得误差 |y(t) – y_final| ≤ SettlingTimeThreshold × |y_final – y_init| 的时间 T。

默认情况下，SettlingTime 衡量误差保持在 |y_final – y_init| 的 2% 以下所需的时间。

Peak - y(t) 的峰值绝对值。

Peak -y(t) – y_init 的峰值绝对值。

此外，输出结构体 S 现在包含一个 TransientTime 字段。该特征包含 R2021b 之前版本中使用的基于峰值误差的稳定时间计算。瞬态时间衡量瞬态动态特性消失的速度。

这些变化也适用于 step、impulse 和 initial 图的特征。此外：

对于 step 图，y_init 始终假定为零，y_final 为稳态值。
对于阶跃响应，对于具有馈通、零点位于原点、具有不稳定零点（欠调）或大超调的模型，瞬态时间和稳定时间往往不同。对于无欠调或无馈通且超调小于 100% 的模型，两者是一致的。有关示例，请参阅阶跃响应中瞬态时间与稳定时间的区别。
对于具有馈通的模型的阶跃响应，新的 RiseTime 值可能会不同，因为默认情况下 y(1) 不为零，而 y_init 为零。在 R2021b 之前，计算的上升时间是从 y(1) 到 y_final 变化区间的 10% 上升到 90% 所需的时间，现在则为从 y_init 到 y_final 变化区间的 10% 上升到 90% 所需的时间。

另请参阅

step | lsiminfo

stepinfo

语法

说明

示例

动态系统的阶跃响应特征

MIMO 系统的阶跃响应特征

指定稳定时间或上升时间的百分比

从响应数据中提取阶跃响应特征

阶跃响应中瞬态时间与稳定时间的区别

具有初始偏移量的数据的阶跃响应特征

输入参数

sys — 动态系统 动态系统模型

y — 阶跃响应数据 向量 | 数组

t — 时间向量 向量

yfinal — 稳态值 标量 | 数组

yinit — 初始值 标量 | 数组

ST — 稳定时间阈值 0.02 (默认) | 0 到 1 之间的标量

RT — 上升时间阈值 [0.1 0.9] (默认) | 2 元素行向量

输出参量

S — 阶跃响应特征 结构体

算法

版本历史记录

R2025a: 计算具有复系数的 LTI 系统的响应特征

R2021b: 响应特征计算变化

另请参阅

`sys` — 动态系统
动态系统模型

`y` — 阶跃响应数据
向量 | 数组

`t` — 时间向量
向量

`yfinal` — 稳态值
标量 | 数组

`yinit` — 初始值
标量 | 数组

`ST` — 稳定时间阈值
0.02 (默认) | 0 到 1 之间的标量

`RT` — 上升时间阈值
`[0.1 0.9]` (默认) | 2 元素行向量

`S` — 阶跃响应特征
结构体