基于问题的模式搜索约束最小化

此示例说明如何使用基于问题的方法中的模式搜索最小化受非线性不等式约束和边界的目标函数。有关该问题基于求解器的版本，请参阅使用基于求解器的模式搜索进行约束最小化。

约束最小化问题

对于这个问题，要最小化的目标函数是二维变量 X 和 Y 的简单函数：

camxy = @(X,Y)(4 - 2.1.*X.^2 + X.^4./3).*X.^2 + X.*Y + (-4 + 4.*Y.^2).*Y.^2;

该函数称为“cam”，如 LCW Dixon 和 GP Szego [1] 中所述。

此外，该问题具有非线性约束和边界。

   x(1)*x(2) + x(1) - x(2) + 1.5 <= 0  (nonlinear constraint)
   10 - x(1)*x(2) <= 0                 (nonlinear constraint)
   0 <= x(1) <= 1                      (bound)
   0 <= x(2) <= 13                     (bound)

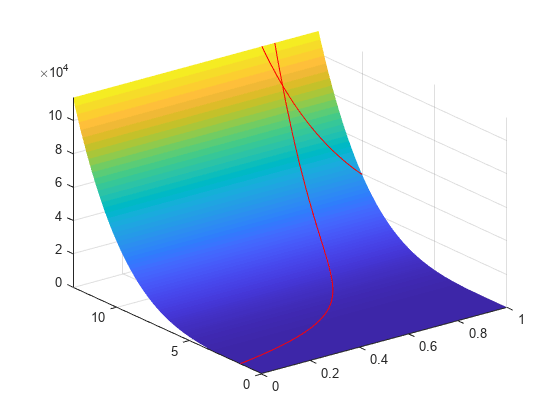
在目标函数的曲面图上绘制非线性约束区域。这些约束将解决解限制在两条红色曲线上方的小区域内。

x1 = linspace(0,1);
y1 = (-x1 - 1.5)./(x1 - 1);
y2 = 10./x1;
[X,Y] = meshgrid(x1,linspace(0,13));
Z = camxy(X,Y);
surf(X,Y,Z,"LineStyle","none")
hold on
z1 = camxy(x1,y1);
z2 = camxy(x1,y2);
plot3(x1,y1,z1,'r-',x1,y2,z2,'r-')
xlim([0 1])
ylim([0 13])
zlim([0,max(Z,[],"all")])
hold off

创建优化变量、问题和约束

为了设置这个问题，创建优化变量 x 和 y。在创建变量时设置边界。

x = optimvar("x","LowerBound",0,"UpperBound",1);
y = optimvar("y","LowerBound",0,"UpperBound",13);

将目标创建为优化表达式。

cam = camxy(x,y);

用这个目标函数创建一个优化问题。

prob = optimproblem("Objective",cam);

创建两个非线性不等式约束，并将它们包含在问题中。

prob.Constraints.cons1 = x*y + x - y + 1.5 <= 0;
prob.Constraints.cons2 = 10 - x*y <= 0;

检查此问题。

show(prob)

  OptimizationProblem : 

	Solve for:
       x, y

	minimize :
       (((((4 - (2.1 .* x.^2)) + (x.^4 ./ 3)) .* x.^2) + (x .* y)) + (((-4) + (4 .* y.^2)) .* y.^2))


	subject to cons1:
       ((((x .* y) + x) - y) + 1.5) <= 0

	subject to cons2:
       (10 - (x .* y)) <= 0

	variable bounds:
       0 <= x <= 1

       0 <= y <= 13

设置初始点并求解

将初始点设置为字段 x 等于 0.5 且 y 等于 0.5 的结构体。

x0.x = 0.5;
x0.y = 0.5;

解决指定 patternsearch 求解器的问题。

[sol,fval] = solve(prob,x0,"Solver","patternsearch")

Solving problem using patternsearch.
Optimization finished: mesh size less than options.MeshTolerance 
and constraint violation is less than options.ConstraintTolerance.

sol = struct with fields:
    x: 0.8122
    y: 12.3122

fval = 9.1324e+04

patternsearch 找到了目标函数值为 9.1324e4 的解点 x = 0.8122, y = 12.3122。

添加可视化

要观察求解器的进度，请指定选择两个绘图函数的选项。绘图函数 psplotbestf 绘制每次迭代中的最佳目标函数值，绘图函数 psplotmaxconstr 绘制每次迭代中的最大约束违反。在元胞数组中设置这两个绘图函数。另外，通过将 Display 选项设置为 'iter'，在命令窗口中显示有关求解器进度的信息。

options = optimoptions(@patternsearch,...
    "PlotFcn",{@psplotbestf,@psplotmaxconstr},...
    "Display","iter");

运行求解器，包括 options 参量。

[sol,fval] = solve(prob,x0,"Solver","patternsearch","Options",options)

Solving problem using patternsearch.

                                      Max
  Iter   Func-count       f(x)      Constraint   MeshSize      Method
    0         1     0.373958         9.75       0.9086    
    1        18       113581    1.617e-10        0.001   Increase penalty
    2       147        92267            0        1e-05   Increase penalty
    3       373      91333.2            0        1e-07   Increase penalty
    4       638        91324            0        1e-09   Increase penalty
Optimization finished: mesh size less than options.MeshTolerance 
and constraint violation is less than options.ConstraintTolerance.

sol = struct with fields:
    x: 0.8122
    y: 12.3122

fval = 9.1324e+04

非线性约束导致 patternsearch 在每次迭代时解决许多子问题。从绘图和迭代显示可以看出，解过程只有几次迭代。但是，迭代显示中的 Func-count 列显示每次迭代有许多函数计算。绘图和迭代显示均表明初始点是不可行的，并且目标函数在初始点处较低。在解过程中，目标函数值先增大，然后减小，直至最终值。

不支持的函数

如果您的目标或非线性约束函数不是优化变量和表达式支持的运算，请使用 fcn2optimexpr 将它们转换为适合基于问题的方法的形式。例如，假设约束 $I_{1} (x) + I_{1} (y) \geq 10$ 取代了约束 $x y \geq 10$ ，其中 $I_{1} (x)$ 是修改后的贝塞尔函数 besseli(1,x)。（贝塞尔函数不是受支持的函数。）使用 fcn2optimexpr 创建此约束，如下所示。首先为 $I_{1} (x) + I_{1} (y)$ 创建一个优化表达式。

bfun = fcn2optimexpr(@(t,u)besseli(1,t) + besseli(1,u),x,y);

接下来，将约束 cons2 替换为约束 bfun >= 10。

prob.Constraints.cons2 = bfun >= 10;

求解。由于约束区域不同，解也不同。

[sol2,fval2] = solve(prob,x0,"Solver","patternsearch","Options",options)

Solving problem using patternsearch.

                                      Max
  Iter   Func-count       f(x)      Constraint   MeshSize      Method
    0         1     0.373958        9.484       0.9307    
    1        18       113581            0        0.001   Increase penalty
    2       183      962.841            0        1e-05   Increase penalty
    3       499      960.942            0        1e-07   Increase penalty
    4       636       960.94            0    8.511e-15   Update multipliers
Optimization finished: mesh size less than options.MeshTolerance 
and constraint violation is less than options.ConstraintTolerance.

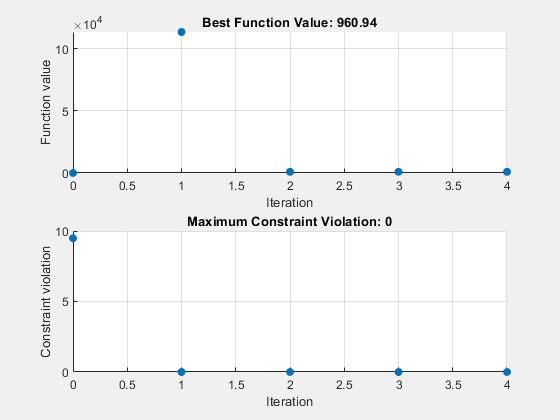
sol2 = struct with fields:
    x: 0.4998
    y: 3.9981

fval2 = 960.9401

参考资料

[1] Dixon, L. C. W., and G .P. Szego (eds.).Towards Global Optimisation 2.North-Holland:Elsevier Science Ltd., Amsterdam, 1978.

另请参阅

patternsearch | solve